Accueil
Nouveaux sujets
Connexion
S'enregistrer
Rechercher
- JPhMMDemi-dieu
Bon ...
- Spoiler:
(EF) étant parallèle à (AB), ABG et EFG sont équilatéraux et CFB est isocèle en F.
Il me semble qu'il faut démontrer que (DE) est médiatrice de [FG] pour conclure que l'angle recherché mesure 30°, mais j'avoue que je n'y arrive pas là tout de suite. Peut-être est-ce la faim qui m'empêche :lol: A tout à l'heure.
Avatar des AbyssesNiveau 8
Même idée que toi JPHMM je pense du coup qu'il suffit de transcrire chaque élément de la première démonstration dans la deuxième.
- Spoiler:
- Dans le deuxieme E joue le role de D et D joue le role de E
_________________
Il y a 10 catégories de personnes ceux qui connaissent le binaire, ceux qui connaissent le ternaire... et les autres.
N'écoutez pas les bruits du monde, mais le silence de l'âme. ( JCVD )
"if you think education is expensive, try ignorance", Abraham Lincoln
Au 01/08/2022 : 2,2 SMIC = 2923,91 euros NET...
Au 01/01/2023 : 2,2 SMIC = 2976,75 euros NET...
Au 01/05/2023 : 2,2 SMIC = 3036,24 euros NET...
Au 01/09/2024 : 2,2 SMIC = 3077,14 euros NET...
Pour info 2,2 SMIC était le salaire des professeurs débutants en 1980.
JPhMMDemi-dieu
Alors,
- Spoiler:
- dans le triangle ABD, on calcule que l'angle ADB mesure 50°, donc ABD est isocèle en A, donc AD = AB. Donc AD = AG, les angles à la base du triangle ADG sont donc égaux à 80°. Or AGB mesure 60°, donc DGF mesure 40°, comme l'angle DFG. Le triangle DFG est donc isocèle en D. Ainsi DFEG est un cerf-volant, ses diagonales sont donc perpendiculaires. (DE) est la médiatrice de [FG], mais aussi la bissectrice de l'angle FEG, donc x = 30°.
_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
- JPhMMDemi-dieu
J'ai eu la révélation en mangeant, d'où mon message ci-dessus.Avatar des Abysses a écrit:Même idée que toi JPHMM je pense du coup qu'il suffit de transcrire chaque élément de la première démonstration dans la deuxième.
- Spoiler:
_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
- JPhMMDemi-dieu
Oui.ycombe a écrit:JPhMM a écrit:Un petit Sangaku de monastère japonais.
Quel est le rayon du grand cercle, sachant que le rayon du petit cercle qui lui est concentrique vaut 1 ?
- Solution:
Si n est le nombre de cercles tangents en couronne, le rayon r du grand cercle est
r = (sec (π/n) + tan (π/n))²
Joli, non?
_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
- JPhMMDemi-dieu
Facile :
Source : http://etudiant.lefigaro.fr/vie-etudiante/news/detail/article/palmares-des-questions-les-plus-difficiles-et-loufoques-posees-en-entretien-d-embauche-19897/
Une corde, plaquée au sol, permet de faire le tour de la Terre autour de l’équateur. On ajoute 1 mètre à cette corde. On obtient donc un cercle un peu plus grand. Une souris pourrait-elle passer sous la corde ?
Source : http://etudiant.lefigaro.fr/vie-etudiante/news/detail/article/palmares-des-questions-les-plus-difficiles-et-loufoques-posees-en-entretien-d-embauche-19897/
_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
InvitéInvité
Oui, avec un rayon moyen de 6400 km, ça fait un espace de l'ordre de 15 cm.JPhMM a écrit:Facile :
Une corde, plaquée au sol, permet de faire le tour de la Terre autour de l’équateur. On ajoute 1 mètre à cette corde. On obtient donc un cercle un peu plus grand. Une souris pourrait-elle passer sous la corde ?
Source : http://etudiant.lefigaro.fr/vie-etudiante/news/detail/article/palmares-des-questions-les-plus-difficiles-et-loufoques-posees-en-entretien-d-embauche-19897/
- JPhMMDemi-dieu
Oui. D'ailleurs, plus simplement :
Le périmètre étant proportionnel au rayon, je n'ai pas besoin de connaître le rayon de la Terre pour calculer le résultat.
Si le rayon est augmenté de 100 cm, le rayon est augmenté de 100 cm / (2pi) = 15,9 cm environ.
Le périmètre étant proportionnel au rayon, je n'ai pas besoin de connaître le rayon de la Terre pour calculer le résultat.
Si le rayon est augmenté de 100 cm, le rayon est augmenté de 100 cm / (2pi) = 15,9 cm environ.
_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
LeclochardEmpereur
Vous vous amusez bien ici. :fou:
J'ai compris que la corde était toujours plaquée au sol alors sa longueur n'a aucune importance pour la souris.
J'ai compris que la corde était toujours plaquée au sol alors sa longueur n'a aucune importance pour la souris.
_________________
Quelqu'un s'assoit à l'ombre aujourd'hui parce que quelqu'un d'autre a planté un arbre il y a longtemps. (W.B)
- JPhMMDemi-dieu
Pourtant l'énoncé dit qu'on obtient un cercle un peu plus grand (que le grand cercle équateur donc).
_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
- InvitéInvité
Il faut imaginer uneune cordeen lévitation, c'est le plus durJPhMM a écrit:Pourtant l'énoncé dit qu'on obtient un cercle un peu plus grand (que le grand cercle équateur donc).
- JPhMMDemi-dieu
C'est pas faux.Will.T a écrit:Il faut imaginer uneune cordeen lévitation, c'est le plus durJPhMM a écrit:Pourtant l'énoncé dit qu'on obtient un cercle un peu plus grand (que le grand cercle équateur donc).
_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
- LeclochardEmpereur
JPhMM a écrit:Pourtant l'énoncé dit qu'on obtient un cercle un peu plus grand (que le grand cercle équateur donc).
Concrètement, sur une longueur de 6400 km (merci Will.T), ajouter un mètre rendra la corde un tout petit peu moins tendue mais elle reposera sur le sol. Où la souris passera-t-elle ?
_________________
Quelqu'un s'assoit à l'ombre aujourd'hui parce que quelqu'un d'autre a planté un arbre il y a longtemps. (W.B)
William FosterExpert
Ça dépend de la taille de la souris...
Variante :
1. Si tous les hommes se donnaient la main, formerions-nous une chaîne assez longue pour faire le tour de la planète ?
2. En ce cas, combien mourraient noyés ?
Variante :
1. Si tous les hommes se donnaient la main, formerions-nous une chaîne assez longue pour faire le tour de la planète ?
2. En ce cas, combien mourraient noyés ?
_________________
Tout le monde me dit que je ne peux pas faire l'unanimité.
"Opinions are like orgasms : mine matters most and I really don't care if you have one." Sylvia Plath
Vérificateur de miroir est un métier que je me verrais bien faire, un jour.
- InvitéInvité
Si on compte 2m d'amplitude par humain, il en faut environ 20 millions pour faire le tour, on a largement de quoi faire.William Foster a écrit:Ça dépend de la taille de la souris...
Variante :
1. Si tous les hommes se donnaient la main, formerions-nous une chaîne assez longue pour faire le tour de la planète ?
2. En ce cas, combien mourraient noyés ?
ylmExpert spécialisé
Je l'ai fait en 6ème il n'y a pas longtemps celui-ci.JPhMM a écrit:Facile :
Une corde, plaquée au sol, permet de faire le tour de la Terre autour de l’équateur. On ajoute 1 mètre à cette corde. On obtient donc un cercle un peu plus grand. Une souris pourrait-elle passer sous la corde ?
J'ai vu passer celui-là sur Twitter récemment:
ABCD est un carré. E=milieu de AD. Le cercle passe par E, C et B. Qui a le + grand périmètre, le carré ou le cercle? pic.twitter.com/jJht7vpurk
— Blogdemaths (@Blogdemaths) 9 avril 2016
- JPhMMDemi-dieu
Sympa
- Spoiler:
- (à toute vitesse)
Soit a la longueur du côté du carré.
Soit H milieu de [BC], et soit I l'autre intersection de (EH) avec le cercle.
EC²=EH²+CH²=a²+0,25a²=1,25a²
et EI/EC = EC/EH d'où EI = EC²/EH = 1,25a
pi*1,25=3,93 environ (centième par excès) d'où le résultat.
_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
- William FosterExpert
C'est la question 2 qui était fun... saboteur de gag !Will.T a écrit:"1. Si tous les hommes se donnaient la main, formerions-nous une chaîne assez longue pour faire le tour de la planète ?
2. En ce cas, combien mourraient noyés ?"
Si on compte 2m d'amplitude par humain, il en faut environ 20 millions pour faire le tour, on a largement de quoi faire.
_________________
Tout le monde me dit que je ne peux pas faire l'unanimité.
"Opinions are like orgasms : mine matters most and I really don't care if you have one." Sylvia Plath
Vérificateur de miroir est un métier que je me verrais bien faire, un jour.
- ylmExpert spécialisé
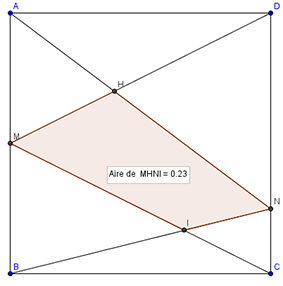
J'ai ça en stock:
ABCD est un carré de côté 1.
M est le milieu de [AD].
BN = 1/4 BC.
Quelle est l'aire du quadrilatère bleu?
ABCD est un carré de côté 1.
M est le milieu de [AD].
BN = 1/4 BC.
Quelle est l'aire du quadrilatère bleu?
- William FosterExpert
- Trop facile :
_________________
Tout le monde me dit que je ne peux pas faire l'unanimité.
"Opinions are like orgasms : mine matters most and I really don't care if you have one." Sylvia Plath
Vérificateur de miroir est un métier que je me verrais bien faire, un jour.
- EmineJe viens de m'inscrire !
L'aire recherchée = 7/30
Il faut d'abord calculer les aires des 4 petits triangles blancs qui ont un côté en commun avec le quadrilatère bleu : 1/10 ; 9/40 ; 1/6 ; 1/24 (On retrouve facilement les mesures des hauteurs grâce à Thalès)
Ensuite il faut faire 0,5 * (1-(1/10)-(9/40)-(1/6)-(1/24)) = 7/30 = 0,233...
Il faut d'abord calculer les aires des 4 petits triangles blancs qui ont un côté en commun avec le quadrilatère bleu : 1/10 ; 9/40 ; 1/6 ; 1/24 (On retrouve facilement les mesures des hauteurs grâce à Thalès)
Ensuite il faut faire 0,5 * (1-(1/10)-(9/40)-(1/6)-(1/24)) = 7/30 = 0,233...
ylm a écrit:J'ai ça en stock:
ABCD est un carré de côté 1.
M est le milieu de [AD].
BN = 1/4 BC.
Quelle est l'aire du quadrilatère bleu?
- ylmExpert spécialisé
Un problème que j'aime bien faire dès la 6ème:
- JPhMMDemi-dieu
Mignon.
Ils trouvent aisément ?
Ils trouvent aisément ?
_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
- ylmExpert spécialisé
Non. C'est un problème que je donne avec des aides et je n'ai jamais vu d'élève trouver sans.
- JPhMMDemi-dieu
Aucun ne pense à "reconstituer" les rectangles par lui-même ?
_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
- ylmExpert spécialisé
Si, j'ai déjà vu ça, mais aucun n'est jamais arrivé à la solution par lui-même.
Permission de ce forum:
Vous ne pouvez pas répondre aux sujets dans ce forum