 JPhMMDemi-dieu
JPhMMDemi-dieu
Problème fourni par Apollonius :
Soit ABCD un rectangle tel que AB = 1 et AD = 2. On nomme O son centre.
Soit (C) un cercle de centre O et de rayon R.
On appelle E et F les intersections de (C) avec respectivement [BA) et [BC).
Quelle doit être la valeur de R pour que E, F et D soient alignés ?
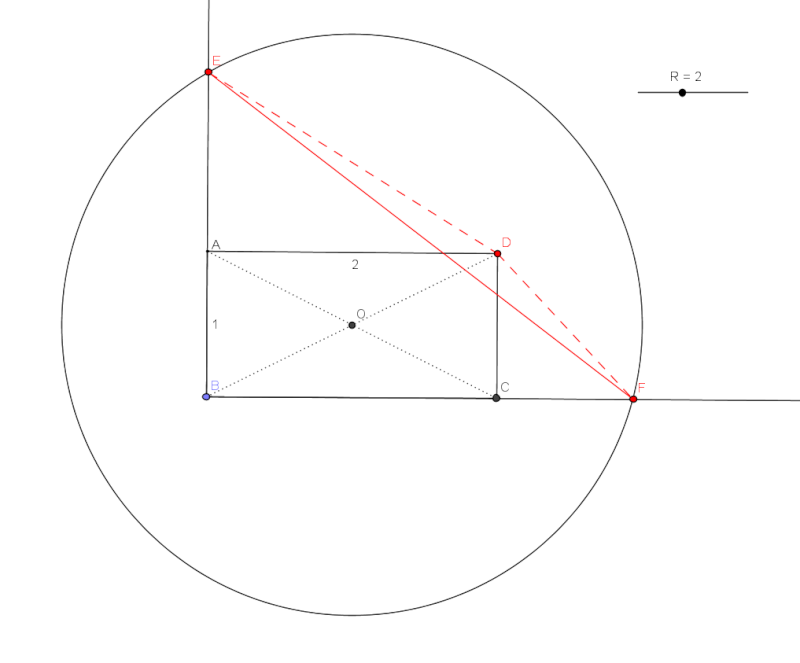
Extension possible : généralisation du problème avec un rectangle de dimensions AB = a et AD = b.
Soit ABCD un rectangle tel que AB = 1 et AD = 2. On nomme O son centre.
Soit (C) un cercle de centre O et de rayon R.
On appelle E et F les intersections de (C) avec respectivement [BA) et [BC).
Quelle doit être la valeur de R pour que E, F et D soient alignés ?

Extension possible : généralisation du problème avec un rectangle de dimensions AB = a et AD = b.
_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
 jonjon71Fidèle du forum
jonjon71Fidèle du forum
Plus exactement (3+racine(33))/4 !
Sauf erreur de calcul, bien sûr...
Merci
Sauf erreur de calcul, bien sûr...
Merci
 IgniatiusGuide spirituel
IgniatiusGuide spirituel
Pour ma part, j'ai trouvé racine(205)/6, soit environ 2,39.
Mais il est tard, je ne sais pas si je me suis planté.
Mais il est tard, je ne sais pas si je me suis planté.
_________________
"Celui qui se perd dans sa passion est moins perdu que celui qui perd sa passion."
St Augustin
"God only knows what I'd be without you"
Brian Wilson
 IgniatiusGuide spirituel
IgniatiusGuide spirituel
Ah si, je me suis planté : c'est en effet très proche de 2,3.
J'ai dû louper un calcul.
On verra ça demain.
J'ai dû louper un calcul.
On verra ça demain.
_________________
"Celui qui se perd dans sa passion est moins perdu que celui qui perd sa passion."
St Augustin
"God only knows what I'd be without you"
Brian Wilson
 JPhMMDemi-dieu
JPhMMDemi-dieu
Jonjon 
Problème : extrait de Sésamath 3e 2008
Problème : extrait de Sésamath 3e 2008
On note 3! (on prononce “factorielle 3”) le produit 1×2×3, on note 4! le produit 1×2×3×4 et ainsi de suite…
Si on calculait le produit 17! que trouverait-on pour les trois derniers chiffres ?
Combien de fois se répète le dernier chiffre de 627! à la fin de ce nombre ?
_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
 IgniatiusGuide spirituel
IgniatiusGuide spirituel
Tu es sûr de la valeur de Jonjon JP ?
Parce qu'elle est plutôt éloignée de ce que l'on trouve via Geogebra...
Je vais m'y remettre ce soir !
Parce qu'elle est plutôt éloignée de ce que l'on trouve via Geogebra...
Je vais m'y remettre ce soir !
_________________
"Celui qui se perd dans sa passion est moins perdu que celui qui perd sa passion."
St Augustin
"God only knows what I'd be without you"
Brian Wilson
 KosakuyosidaNiveau 5
KosakuyosidaNiveau 5
Bon le dernier chiffre est un $0$... et plus généralement, le nombre $n!$ se termine par $E(\dfrac{n}{5})+E(\dfrac{n}{5^2})+...+E(\dfrac{n}{5^p})$ zéros tant que $E(\dfrac{n}{5^p})$ n'est pas nul. Dans le cas de $627!$, le nombre de zéros est:
- Spoiler:
- $156$.
_________________
Bien informés, les hommes sont des citoyens ; mal informés, ils deviennent des sujets.
Alfred Sauvy.
 KosakuyosidaNiveau 5
KosakuyosidaNiveau 5
Question bonus: quel est le dernier chiffre non nul de $n!$ ? 
_________________
Bien informés, les hommes sont des citoyens ; mal informés, ils deviennent des sujets.
Alfred Sauvy.
 JPhMMDemi-dieu
JPhMMDemi-dieu
Je ne suis jamais sûr d'un calcul.Igniatius a écrit:Tu es sûr de la valeur de Jonjon JP ?
Parce qu'elle est plutôt éloignée de ce que l'on trouve via Geogebra...
Je vais m'y remettre ce soir !
Effectivement, Gégé donne une valeur proche de 2,315. Notre calcul doit être erroné.
Hop, on recommence...
_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
 JPhMMDemi-dieu
JPhMMDemi-dieu
On a le droit de tricher ?Kosakuyosida a écrit:Question bonus: quel est le dernier chiffre non nul de $n!$ ?
- Spoiler:
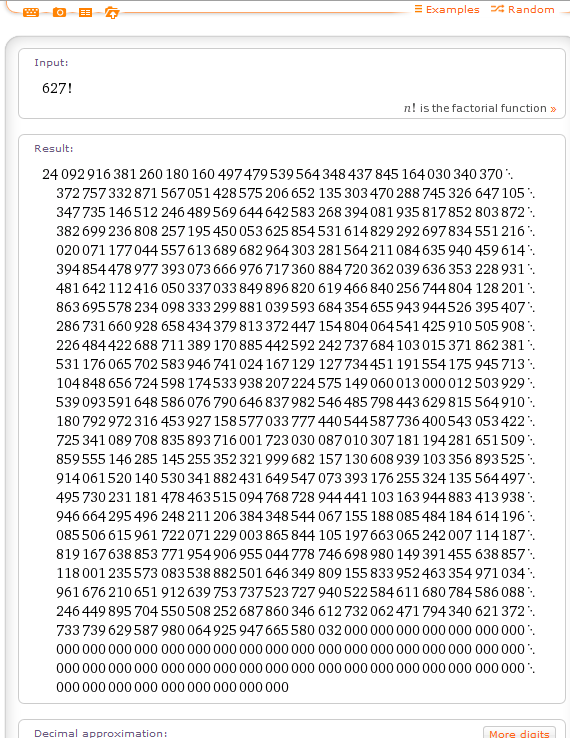
:lol!:
PS : Oui, c'est bien 125 + 25 + 5 + 1 = 156 bien sûr.
_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
 KosakuyosidaNiveau 5
KosakuyosidaNiveau 5
Mais tu ne réponds pas à la question !JPhMM a écrit:On a le droit de tricher ?Kosakuyosida a écrit:Question bonus: quel est le dernier chiffre non nul de $n!$ ?

- Spoiler:
_________________
Bien informés, les hommes sont des citoyens ; mal informés, ils deviennent des sujets.
Alfred Sauvy.
 JPhMMDemi-dieu
JPhMMDemi-dieu
Oups, ça s'est vu 
Je cherche.
Je cherche.

_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
 JPhMMDemi-dieu
JPhMMDemi-dieu
_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
 InvitéInvité
InvitéInvité
 JPhMMDemi-dieu
JPhMMDemi-dieu
_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
 JPhMMDemi-dieu
JPhMMDemi-dieu
Alors...Kosakuyosida a écrit:Question bonus: quel est le dernier chiffre non nul de $n!$ ?
Je n'ai pas encore trouvé, mais j'ai la bonne piste je crois. Simplement il est tard, et je n'ai plus le cerveau à ça.
Je vais essayer de l'écrire simplement, pour ceux qui ne sont pas profs de maths.
Le produit de deux nombres entiers a pour chiffre des unités le chiffre des unités du produit des chiffres des unités des deux nombres.
Par exemple : 324*1598 finit par un 2 car 4*8 finit par un 2.
De plus 10! = (3*4*6*7*8*9) * (2*5*10) = 36288 * 100
Donc le dernier chiffre non nul de 20! est 4 car 8 * 8 = 64
MAIS le dernier chiffre non nul de 30! n'est pas 2 malgré le fait que 8 * 4 = 32.
En effet, 20 et 30 encadrent un diviseur d'une puissance de 10, puisque 25 * 4 = 100, etc.
Me reste donc à mettre tout ça en forme...
_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
 ZorglubHabitué du forum
ZorglubHabitué du forum
Y'a-t-il une solution géométrie élégante et habile ou bien faut-il bouriner analytiquement ?
 JPhMMDemi-dieu
JPhMMDemi-dieu
J'ai cherché une solution élégante, je n'en ai pas trouvée, ce qui ne signifie pas qu'elle n'existe pas — d'ailleurs, je suis convaincu qu'il doit y avoir une solution géométrique. Si d'aventure vous en trouvez une, elle m'intéresse beaucoup. 
Tout de même, du fait de la racine cubique de 2, d'après le théorème de Wantzel (voir duplication du cube), il n'existe pas de solution à la règle et au compas.

Tout de même, du fait de la racine cubique de 2, d'après le théorème de Wantzel (voir duplication du cube), il n'existe pas de solution à la règle et au compas.
_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
 ZorglubHabitué du forum
ZorglubHabitué du forum
Je crains de ne pas avoir ce talent !
En plus je préfère perdre mon temps sur les forums à dire des conneries pour agacer les uns ou les autres !
En plus je préfère perdre mon temps sur les forums à dire des conneries pour agacer les uns ou les autres !
 JPhMMDemi-dieu
JPhMMDemi-dieu
Je comprends, étant atteint du même mal.Zorglub a écrit:En plus je préfère perdre mon temps sur les forums à dire des conneries pour agacer les uns ou les autres !
_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
 adelaideaugustaFidèle du forum
adelaideaugustaFidèle du forum
JPhMM a écrit:Je comprends, étant atteint du même mal.Zorglub a écrit:En plus je préfère perdre mon temps sur les forums à dire des conneries pour agacer les uns ou les autres !
C'est pas beau, vous êtes addicts !



Permission de ce forum:
Vous ne pouvez pas répondre aux sujets dans ce forum




