- JPhMMDemi-dieu
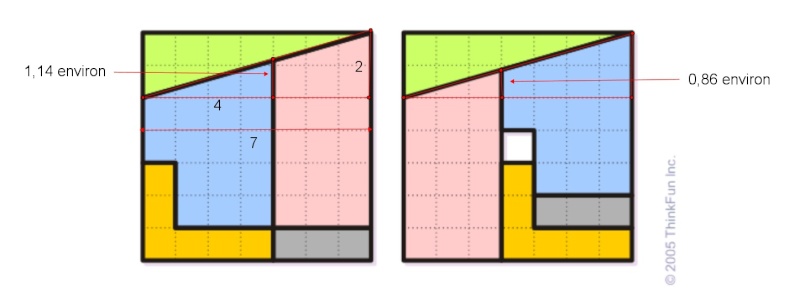
Figure de gauche :
Aire (rose) = 3 x (6 + (8/7 + 4)) / 2 = 117/7
Aire (bleu) = 4 x (4 + (8/7 + 4)) / 2 - 2 = 114/7
Somme des deux = 33
Figure de droite :
Aire (rose) = 3 x (5 + (6/7 + 5)) / 2 = 114/7
Aire (bleu) = 4 x (5 + (6/7 + 3)) /2 - 2 = 110/7
Somme des deux = 32
CQFD
Merci pour le problème

 JPhMMDemi-dieu
JPhMMDemi-dieu
Plus intuitivement :
Le "1,14 environ" est en fait 4x2/7 = 8/7 (Thalès).
Le "0,86 environ" est en fait 3x2/7 = 6/7
Le rose et le bleu sont rabotés d'une hauteur de 1/7, c'est-à-dire qu'ils perdent une aire totale (parallélogramme) de 1/7 x 7 = 1.
Le "1,14 environ" est en fait 4x2/7 = 8/7 (Thalès).
Le "0,86 environ" est en fait 3x2/7 = 6/7
Le rose et le bleu sont rabotés d'une hauteur de 1/7, c'est-à-dire qu'ils perdent une aire totale (parallélogramme) de 1/7 x 7 = 1.
_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
 JPhMMDemi-dieu
JPhMMDemi-dieu
Je viens de comprendre.ycombe a écrit:JPhMM a écrit:Le plus simplement possible : les figures roses et bleues sont "rabotées" en haut dans la seconde configuration, de sorte qu'on perd l'équivalent d'un carreau au total.
J'aurais pas dit ça. Pour moi ça dépasse un peu, ce qui fait que ce n'est plus un carré. Le bas dépasse de l'équivalent d'un petit carré.
Tu parles à figures superposables (découpage).
Je considérais les deux dessins proposés.
Mais oui, cela revient au même.
_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
 ycombeMonarque
ycombeMonarque
Voilà. Moi, j'ai trouvé en déplaçant les figures dans ma tête.JPhMM a écrit:Je viens de comprendre.ycombe a écrit:JPhMM a écrit:Le plus simplement possible : les figures roses et bleues sont "rabotées" en haut dans la seconde configuration, de sorte qu'on perd l'équivalent d'un carreau au total.
J'aurais pas dit ça. Pour moi ça dépasse un peu, ce qui fait que ce n'est plus un carré. Le bas dépasse de l'équivalent d'un petit carré.
Tu parles à figures superposables (découpage).
Je considérais les deux dessins proposés.
Mais oui, cela revient au même.

_________________
Assurbanipal: "Passant, mange, bois, divertis-toi ; tout le reste n’est rien".
Franck Ramus : "Les sciences de l'éducation à la française se font fort de produire un discours savant sur l'éducation, mais ce serait visiblement trop leur demander que de mettre leur discours à l'épreuve des faits".
 ycombeMonarque
ycombeMonarque
Pour ceux qui aiment le chocolat:
- Spoiler:
- Explication:
_________________
Assurbanipal: "Passant, mange, bois, divertis-toi ; tout le reste n’est rien".
Franck Ramus : "Les sciences de l'éducation à la française se font fort de produire un discours savant sur l'éducation, mais ce serait visiblement trop leur demander que de mettre leur discours à l'épreuve des faits".
 JPhMMDemi-dieu
JPhMMDemi-dieu
Somptueux !!!!!
_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
 ycombeMonarque
ycombeMonarque
JPhMM a écrit:Je viens de comprendre.ycombe a écrit:JPhMM a écrit:Le plus simplement possible : les figures roses et bleues sont "rabotées" en haut dans la seconde configuration, de sorte qu'on perd l'équivalent d'un carreau au total.
J'aurais pas dit ça. Pour moi ça dépasse un peu, ce qui fait que ce n'est plus un carré. Le bas dépasse de l'équivalent d'un petit carré.
Tu parles à figures superposables (découpage).
Je considérais les deux dessins proposés.
Mais oui, cela revient au même.
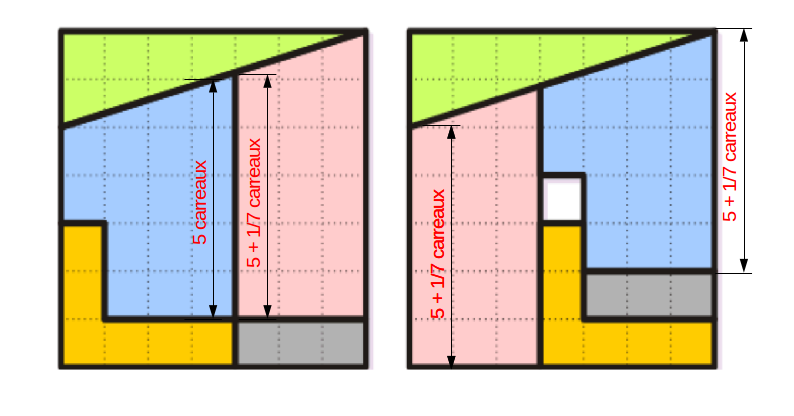
Voilà. Pour moi ça dépasse à droite.
_________________
Assurbanipal: "Passant, mange, bois, divertis-toi ; tout le reste n’est rien".
Franck Ramus : "Les sciences de l'éducation à la française se font fort de produire un discours savant sur l'éducation, mais ce serait visiblement trop leur demander que de mettre leur discours à l'épreuve des faits".
 JPhMMDemi-dieu
JPhMMDemi-dieu
Je t'ai déjà proposé le problème de la fourmi rouge ?
Des fourmis noires les unes derrière les autres forment une colonne d'un mètre de long.
Une fourmi rouge ferme la marche.
La colonne de fourmis noires se déplace de façon rectiligne et avance ainsi d'un mètre.
Dans le même temps, la fourmi rouge (plus rapide donc) longe la colonne pour atteindre le début de la colonne, puis la longe de nouveau, dans l'autre sens, pour revenir à la fin de la colonne.
Sachant que toutes les fourmis se déplacent à vitesse constante, quelle distance a parcouru la fourmi rouge ?
Des fourmis noires les unes derrière les autres forment une colonne d'un mètre de long.
Une fourmi rouge ferme la marche.
La colonne de fourmis noires se déplace de façon rectiligne et avance ainsi d'un mètre.
Dans le même temps, la fourmi rouge (plus rapide donc) longe la colonne pour atteindre le début de la colonne, puis la longe de nouveau, dans l'autre sens, pour revenir à la fin de la colonne.
Sachant que toutes les fourmis se déplacent à vitesse constante, quelle distance a parcouru la fourmi rouge ?
_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
 ycombeMonarque
ycombeMonarque
JPhMM a écrit:Je t'ai déjà proposé le problème de la fourmi rouge ?
Des fourmis noires les unes derrière les autres forment une colonne d'un mètre de long.
Une fourmi rouge ferme la marche.
La colonne de fourmis noires se déplace de façon rectiligne et avance ainsi d'un mètre.
Dans le même temps, la fourmi rouge (plus rapide donc) longe la colonne pour atteindre le début de la colonne, puis la longe de nouveau, dans l'autre sens, pour revenir à la fin de la colonne.
Sachant que toutes les fourmis se déplacent à vitesse constante, quelle distance a parcouru la fourmi rouge ?
1+√2 m ?
_________________
Assurbanipal: "Passant, mange, bois, divertis-toi ; tout le reste n’est rien".
Franck Ramus : "Les sciences de l'éducation à la française se font fort de produire un discours savant sur l'éducation, mais ce serait visiblement trop leur demander que de mettre leur discours à l'épreuve des faits".
 User25249Niveau 5
User25249Niveau 5
JPhMM a écrit:Je t'ai déjà proposé le problème de la fourmi rouge ?
Des fourmis noires les unes derrière les autres forment une colonne d'un mètre de long.
Une fourmi rouge ferme la marche.
La colonne de fourmis noires se déplace de façon rectiligne et avance ainsi d'un mètre.
Dans le même temps, la fourmi rouge (plus rapide donc) longe la colonne pour atteindre le début de la colonne, puis la longe de nouveau, dans l'autre sens, pour revenir à la fin de la colonne.
Sachant que toutes les fourmis se déplacent à vitesse constante, quelle distance a parcouru la fourmi rouge ?
Je dirais ça :
- Spoiler:
- 3 mètres : 2 x la longueur de la colonne + son déplacement
 JPhMMDemi-dieu
JPhMMDemi-dieu
ycombe a écrit:JPhMM a écrit:Je t'ai déjà proposé le problème de la fourmi rouge ?
Des fourmis noires les unes derrière les autres forment une colonne d'un mètre de long.
Une fourmi rouge ferme la marche.
La colonne de fourmis noires se déplace de façon rectiligne et avance ainsi d'un mètre.
Dans le même temps, la fourmi rouge (plus rapide donc) longe la colonne pour atteindre le début de la colonne, puis la longe de nouveau, dans l'autre sens, pour revenir à la fin de la colonne.
Sachant que toutes les fourmis se déplacent à vitesse constante, quelle distance a parcouru la fourmi rouge ?
1+√2 m ?
_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
 JPhMMDemi-dieu
JPhMMDemi-dieu
Non.Stéphane60150 a écrit:JPhMM a écrit:Je t'ai déjà proposé le problème de la fourmi rouge ?
Des fourmis noires les unes derrière les autres forment une colonne d'un mètre de long.
Une fourmi rouge ferme la marche.
La colonne de fourmis noires se déplace de façon rectiligne et avance ainsi d'un mètre.
Dans le même temps, la fourmi rouge (plus rapide donc) longe la colonne pour atteindre le début de la colonne, puis la longe de nouveau, dans l'autre sens, pour revenir à la fin de la colonne.
Sachant que toutes les fourmis se déplacent à vitesse constante, quelle distance a parcouru la fourmi rouge ?
Je dirais ça :
- Spoiler:
Ce serait trop simple.

_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
 ycombeMonarque
ycombeMonarque
JPhMM a écrit:ycombe a écrit:JPhMM a écrit:Je t'ai déjà proposé le problème de la fourmi rouge ?
Des fourmis noires les unes derrière les autres forment une colonne d'un mètre de long.
Une fourmi rouge ferme la marche.
La colonne de fourmis noires se déplace de façon rectiligne et avance ainsi d'un mètre.
Dans le même temps, la fourmi rouge (plus rapide donc) longe la colonne pour atteindre le début de la colonne, puis la longe de nouveau, dans l'autre sens, pour revenir à la fin de la colonne.
Sachant que toutes les fourmis se déplacent à vitesse constante, quelle distance a parcouru la fourmi rouge ?
1+√2 m ?


Par l'algèbre. J'aime bien faire autrement mais là, je n'avais pas d'autres idées.
_________________
Assurbanipal: "Passant, mange, bois, divertis-toi ; tout le reste n’est rien".
Franck Ramus : "Les sciences de l'éducation à la française se font fort de produire un discours savant sur l'éducation, mais ce serait visiblement trop leur demander que de mettre leur discours à l'épreuve des faits".
 User25249Niveau 5
User25249Niveau 5
Non.JPhMM a écrit:
Je dirais ça :
- Spoiler:
Ce serait trop simple.
 [/quote]
[/quote]Je me disais aussi

 JPhMMDemi-dieu
JPhMMDemi-dieu
Oui, il serait très joli de trouver une réponse géométrique.ycombe a écrit:JPhMM a écrit:ycombe a écrit:
1+√2 m ?


Par l'algèbre. J'aime bien faire autrement mais là, je n'avais pas d'autres idées.
_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
 jaybeNiveau 9
jaybeNiveau 9
Il y a toujours la possibilité de paramétrer le temps selon une nouvelle dimension... il y a le célèbre problème des marcheurs à vitesse constante pour illustrer cette possibilité.
_________________
Les mathématiciens ne sont pas des gens qui trouvent les mathématiques faciles ; comme tout le monde, ils savent qu'elles sont difficiles, mais ça ne leur fait pas peur !
 jaybeNiveau 9
jaybeNiveau 9
un truc bricolé vite fait... la somme des distances GC + CH semble bien correspondre à $1+\sqrt{2}$ 

_________________
Les mathématiciens ne sont pas des gens qui trouvent les mathématiques faciles ; comme tout le monde, ils savent qu'elles sont difficiles, mais ça ne leur fait pas peur !
 ycombeMonarque
ycombeMonarque
Geogebra est vraiment très laid.
J'ai eu la même idée, mais comment prouves-tu la longueur totale?
J'ai eu la même idée, mais comment prouves-tu la longueur totale?
_________________
Assurbanipal: "Passant, mange, bois, divertis-toi ; tout le reste n’est rien".
Franck Ramus : "Les sciences de l'éducation à la française se font fort de produire un discours savant sur l'éducation, mais ce serait visiblement trop leur demander que de mettre leur discours à l'épreuve des faits".
 jaybeNiveau 9
jaybeNiveau 9
Pour montrer que la longueur est celle souhaitée, on peut ajouter un point J de sorte que C soit le milieu de [HJ], donc maintenant la longueur recherchée est directement GJ ; si on construit indépendamment un segment [KL] ayant la bonne longueur (par exemple en prolongeant d'une unité la diagonale d'un carré de coté 1), on pourra utiliser le bouton "relation a=b" sur les segments [GJ] et [KL] et normalement geogebra répondra qu'ils sont de même longueur. Mais je pense qu'on peut faire mieux que ça, je cherche...
_________________
Les mathématiciens ne sont pas des gens qui trouvent les mathématiques faciles ; comme tout le monde, ils savent qu'elles sont difficiles, mais ça ne leur fait pas peur !
 BrindIfFidèle du forum
BrindIfFidèle du forum
En calculant les rapports entre les longueurs, on trouve des équations qui mènent au même résultat qu'avec une analyse algébrique plus directe du problème, mais du coup la solution n'est pas plus satisfaisante :gratte:ycombe a écrit:J'ai eu la même idée, mais comment prouves-tu la longueur totale?
(En prenant HG comme unité et I point d'intersection de (AC) et (BH) : BI+2IH=1 ; IH/BI=HC ; HC=BI+IH)
 FreitterNiveau 1
FreitterNiveau 1
Bonjour, pour ceux qui aiment se casser un peu la tête, je recommande le site diophante.fr, avec de nombreux nouveaux problèmes chaque mois !
 JPhMMDemi-dieu
JPhMMDemi-dieu
J'ai cherché très fort, fait plein de dessins, je n'arrive pas à trouver la démonstration géométrique qui utilise de façon simple la somme de la longueur du côté du carré de côté 1 et de sa diagonale (ou plus probablement de deux demi-diagonales de ce carré). Mais je ne désespère pas.jaybe a écrit:Pour montrer que la longueur est celle souhaitée, on peut ajouter un point J de sorte que C soit le milieu de [HJ], donc maintenant la longueur recherchée est directement GJ ; si on construit indépendamment un segment [KL] ayant la bonne longueur (par exemple en prolongeant d'une unité la diagonale d'un carré de coté 1), on pourra utiliser le bouton "relation a=b" sur les segments [GJ] et [KL] et normalement geogebra répondra qu'ils sont de même longueur. Mais je pense qu'on peut faire mieux que ça, je cherche...
_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
 jaybeNiveau 9
jaybeNiveau 9
Je viens de reprendre le problème ; on peut réaliser la construction sur geogebra en construisant les points A(0,0), B(0,1) et librement le point D, de sorte que les autres points soient liés à D. En plaçant de façon convenablement choisie ce point, on peut s'arranger pour que le point F ait une ordonnée égale à 1 et que les droites (CF) et (CI) soient perpendiculaires (ce qui correspond à l'alignement des points A, C et I). Les sommets F, C et I forment 4 sommets du carré de coté 1 recherché et la distance totale parcourue par la fourmi correspond à la longueur IJ (ajouter le point J à l'intersection des droites (AG) et (FI)). [non, zut, j'ai mélangé deux points, je modifie !]
_________________
Les mathématiciens ne sont pas des gens qui trouvent les mathématiques faciles ; comme tout le monde, ils savent qu'elles sont difficiles, mais ça ne leur fait pas peur !
 jaybeNiveau 9
jaybeNiveau 9
Voici l'image qu'on obtient (sauf que tous les noms des points ont changé entre temps, gloups !) 

_________________
Les mathématiciens ne sont pas des gens qui trouvent les mathématiques faciles ; comme tout le monde, ils savent qu'elles sont difficiles, mais ça ne leur fait pas peur !
 jaybeNiveau 9
jaybeNiveau 9
Pour vous faire chercher un peu : c'est une conjecture, supposée vraie pour tout entier naturel non nul pendant quelques décennies, mais on a montré au cours du vingtième siècle (en plusieurs temps) qu'elle était fausse pour des nombres un peu plus petits qu'un milliard...
_________________
Les mathématiciens ne sont pas des gens qui trouvent les mathématiques faciles ; comme tout le monde, ils savent qu'elles sont difficiles, mais ça ne leur fait pas peur !
 JPhMMDemi-dieu
JPhMMDemi-dieu
Ce n'est pas la conjecture de Mertens, semble-t-il...


_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
- Donner une culture mathématique à un enfant de 7 ans
- Le problème du chameau (ouvert à tous bien sur ^^ )
- Stage TZR Créteil + réunion mutation : ouvert à tous!
- PISA 2012 : baisse des performances des élèves de 15 ans en culture mathématique et augmentation des inégalités scolaires en France
- Stage TZR SNES Créteil le vendredi 22 mars 2013 ouvert à tous !!!
Permission de ce forum:
Vous ne pouvez pas répondre aux sujets dans ce forum




