Jeu : quizz de culture mathématique, ouvert à tous :D

Je me permets de revenir un peu-beaucoup en arrière sur cette question (parce qu'elle m'a tracassée...) :

Comment écrire avec un nombre minimal de signes le nombre 0,99999999999... ?

Réponse :

1

Démonstration :

Igniatius a écrit:Soit x=0,99999.....
10x=9,99999.........
Donc 10x-x=9
Soit 9x=9
Soit x=1.

Au départ, je me suis dit : c'est pas possible, ça tend vers 1, mais ça n'est jamais égal à 1.
Et puis je regarde la démonstration : elle a l'air imparable. Zut ! J'ai dû rien piger aux asymptotes.

Mais il n'y aurait pas un bug ?

Quand tu multiplies tout par 10, à la deuxième ligne, tu décales la virgule vers la droite : donc il y a un 9 en moins (soit l'infini moins 1, si je puis dire...).
Et ensuite, à la 3ème ligne, tu soustrais un nombre x qui à un 9 de plus...



Le résultat pour 9x ne serait pas 9, mais 8,99999(...)999991

?

Mufab, tu n'as pas bien compris la notion d'infini...

Mufab a écrit:Quand tu multiplies tout par 10, à la deuxième ligne, tu décales la virgule vers la droite : donc il y a un 9 en moins (soit l'infini moins 1, si je puis dire...).
Et ensuite, à la 3ème ligne, tu soustrais un nombre x qui à un 9 de plus...



Le résultat pour 9x ne serait pas 9, mais 8,99999(...)999991

?

Non. Il y en a autant.

Mufab, tu n'as pas bien compris la notion d'infini...

Ben peut-être. (C'est pas grave, hein ?)

Mais je n'arrive pas à concevoir 0,999999... comme égal à 1.

hs:ton avatar me fait peur JP!

Question : quel est l'ensemble le plus « grand » parmi ceux-ci :
* l'ensemble des nombres entiers naturels ;
* l'ensemble des nombres entiers relatifs ;
* l'ensemble des nombres entiers naturels pairs ;
* l'ensemble des nombres premiers ;
* l'ensemble des nombres rationnels ;
* l'ensemble des nombres décimaux ?

thrasybule a écrit:hs:ton avatar me fait peur JP!

Et oui, c'est intéressant comme question.
Je le fais tjrs avec mes secondes en début d'année afin de leur montrer que ce qu'ils croient avoir compris à l'infini est plus complexe que leur interprétation.
En fait, il faut que tu t'interroges sur la signification des ... à la fin d'une écriture décimale.
Je peux te l'expliquer à peu près convenablement avec la notion de série mais je ne suis pas certain que tu l'aies vue : l'écriture 0,99999.... est en fait la limite d'une somme finie lorsque le nombre de termes tend vers + l'infini.
Plus précisément :
0,999...= lim(qd n tend vers +infini) de la somme pour k allant de 1 à n des 9/(10^k)
S'il y avait un émulateur LaTex sur Neoprofs, ce serait cool !

Après, il suffit d'effectuer les opérations sur cette limite.

Mufab a écrit:

Mufab, tu n'as pas bien compris la notion d'infini...

Ben peut-être. (C'est pas grave, hein ?)

Mais je n'arrive pas à concevoir 0,999999... comme égal à 1.

Quel sens donnes-tu à l'écriture 0,99999..... ?
C'est la vraie question.

Et ce n'est pas une mince question, rassure-toi.

Ignatius : à quoi ça sert que JPhMM se décarcasse ?

https://www.neoprofs.org/t32895-inserer-des-formules-mathematiques-et-des-courbes-dans-le-forum?highlight=math%E9matiques

JPhMM a écrit:Question : quel est l'ensemble le plus « grand » parmi ceux-ci :
* l'ensemble des nombres entiers naturels ;
* l'ensemble des nombres entiers relatifs ;
* l'ensemble des nombres entiers naturels pairs ;
* l'ensemble des nombres premiers ;
* l'ensemble des nombres rationnels ;
* l'ensemble des nombres décimaux ?

ben comme ils contiennent tous une infinité de nombre, ils n'y en a pas un plus grand que les autres non ?

Mufab a écrit:

Mufab, tu n'as pas bien compris la notion d'infini...

Ben peut-être. (C'est pas grave, hein ?)

Mais je n'arrive pas à concevoir 0,999999... comme égal à 1.

1 / 3 = 0,3333333.....

Mais alors, simple question :
0,33333333... x 3 = ?

Remarque importante : ce n'est pas du tout une démonstration, simplement une... invitation à concevoir.

Igniatius a écrit:

Mufab a écrit:

Mufab, tu n'as pas bien compris la notion d'infini...

Ben peut-être. (C'est pas grave, hein ?)

Mais je n'arrive pas à concevoir 0,999999... comme égal à 1.

Quel sens donnes-tu à l'écriture 0,99999..... ?
C'est la vraie question.

Et ce n'est pas une mince question, rassure-toi.

et pou un prof de physique, on n'a même pas besoin d'autant de 9 pour dire que c'est égal à 1...

Will.T a écrit:

JPhMM a écrit:Question : quel est l'ensemble le plus « grand » parmi ceux-ci :
* l'ensemble des nombres entiers naturels ;
* l'ensemble des nombres entiers relatifs ;
* l'ensemble des nombres entiers naturels pairs ;
* l'ensemble des nombres premiers ;
* l'ensemble des nombres rationnels ;
* l'ensemble des nombres décimaux ?

ben comme ils contiennent tous une infinité de nombre, ils n'y en a pas un plus grand que les autres non ?

Ah ah ah ! Je laisse JP te faire un exposé : ta réponse est correcte, mais la justification totalement fausse.
Je crois que tu n'as pas bien compris la notion d'infini... :lol:

Question Will : quel est l'ensemble le plus « grand » parmi ceux-ci :
* l'ensemble des nombres entiers naturels ;
* l'ensemble des nombres entiers relatifs ;
* l'ensemble des nombres entiers naturels pairs ;
* l'ensemble des nombres premiers ;
* l'ensemble des nombres rationnels ;
* l'ensemble des nombres décimaux ;
* l'ensemble des nombres de l'intervalle [0 ; 1] (notez que cet ensemble, c'est l'intervalle lui-même, bien sûr) ?

Accessoirement :
* l'ensemble des nombres réels ?
* l'ensemble des nombres irrationnels ?

Pire :
* l'ensemble des nombres complexes ?

1 / 3 = 0,3333333.....

Mais alors, simple question :
0,33333333... x 3 = ?

Ben justement.
1/3, c'est 1/3... Et l'écriture = 0,333333333... Pour moi, elle n'est qu'approximative.

Donc 0,3333333... x3 = 0,9999999...

Et (1/3) x 3 = 1. ça d'accord.

Bon, d'un autre côté, je ne suis qu'une instit de base. Donc je m'incline.

Spoiler:

John a écrit:Ignatius : à quoi ça sert que JPhMM se décarcasse ?

https://www.neoprofs.org/t32895-inserer-des-formules-mathematiques-et-des-courbes-dans-le-forum?highlight=math%E9matiques

Ah j'avais pas vu, très bien, merci big brother !

Ce que je voulais dire pour Mufab donc :
[img]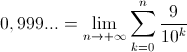[/img]

l'écriture = 0,333333333... Pour moi, elle n'est approximative

Non : elle est exacte.
L'écriture approximative c'est 0,3333333333., pas 0,333333333...

Mufab a écrit:

1 / 3 = 0,3333333.....

Mais alors, simple question :
0,33333333... x 3 = ?

Ben justement.
1/3, c'est 1/3... Et l'écriture = 0,333333333... Pour moi, elle n'est approximative.

Donc 0,3333333... x3 = 0,9999999...

Et (1/3) x 3 = 1. ça d'accord.

Bon, d'un autre côté, je ne suis qu'une instit de base. Donc je m'incline.

Spoiler:

0,3333... n'est pas l'écriture de l'approximation du nombre 1/3, mais tant que certaines choses ne sont pas définies (le développement décimal illimité d'un nombre réel, pour dire les choses clairement), c'est une écriture (conceptuellement) approximative d'un nombre qui n'est pas une approximation, c'est vrai.

bon alors, qu'est ce qu'il y a de faux dans ce que j'ai écrit ???

Igniatius a écrit:

Mufab a écrit:

Mufab, tu n'as pas bien compris la notion d'infini...

Ben peut-être. (C'est pas grave, hein ?)

Mais je n'arrive pas à concevoir 0,999999... comme égal à 1.

Quel sens donnes-tu à l'écriture 0,99999..... ?
C'est la vraie question.

Pour moi, c'est un nombre qui se rapproche de un (aussi près qu'il peut), mais qui n'y arrive jamais. Il le touche presque, purée, mais non : il manquera toujours un chouille.

Et entre l'intervalle [0 ; 1] et l'intervalle [0 ; 1 [ qui a le plus de nombres ?

Will.T a écrit:

JPhMM a écrit:Question : quel est l'ensemble le plus « grand » parmi ceux-ci :
* l'ensemble des nombres entiers naturels ;
* l'ensemble des nombres entiers relatifs ;
* l'ensemble des nombres entiers naturels pairs ;
* l'ensemble des nombres premiers ;
* l'ensemble des nombres rationnels ;
* l'ensemble des nombres décimaux ?

ben comme ils contiennent tous une infinité de nombre, ils n'y en a pas un plus grand que les autres non ?

Tous ces ensembles sont en bijection. Ils ont la cardinalité du dénombrable. En clair, on peut les compter les nombres qu'ils contiennent, un après l'autre, même si c'est un peu compliqué parfois.
Par contre, qu'ils soient en quantité infinie ne permet pas de dire que ces quantités soient "égales" (on dit équipotentes). Parce qu'il y a des infinis plus grands que d'autres.

Ainsi, il y a plus de nombres dans l'intervalle [0 ; 1] que dans l'ensemble des nombres décimaux.

Mufab a écrit:

Igniatius a écrit:

Mufab a écrit:

Mufab, tu n'as pas bien compris la notion d'infini...

Ben peut-être. (C'est pas grave, hein ?)

Mais je n'arrive pas à concevoir 0,999999... comme égal à 1.

Quel sens donnes-tu à l'écriture 0,99999..... ?
C'est la vraie question.

Pour moi, c'est un nombre qui se rapproche de un (aussi près qu'il peut), mais qui n'y arrive jamais. Il le touche presque, purée, mais non : il manquera toujours un chouille.

Non seulement un chouille aussi petit que tu veux, mais aussi un chouille nul. Non pas seulement un infini potentiel, mais un infini actuel, et telle est effectivement la difficulté.

Mufab a écrit:

Igniatius a écrit:

Mufab a écrit:

Mufab, tu n'as pas bien compris la notion d'infini...

Ben peut-être. (C'est pas grave, hein ?)

Mais je n'arrive pas à concevoir 0,999999... comme égal à 1.

Quel sens donnes-tu à l'écriture 0,99999..... ?
C'est la vraie question.

Pour moi, c'est un nombre qui se rapproche de un (aussi près qu'il peut), mais qui n'y arrive jamais. Il le touche presque, purée, mais non : il manquera toujours un chouille.

Très intéressant.
Quel est l'écart entre 1 et 0,9 ? Entre 1 et 0,99 ? Entre 1 et 0,999 ?
Que penses-tu donc de l'écart entre 1 et 0,9999.... qui est donc inférieur à chacun des précédents ?

Kupo a écrit:Et entre l'intervalle [0 ; 1] et l'intervalle [0 ; 1 [ qui a le plus de nombres ?

Demandons à Zénon d'Elée
Lions les deux questions actuelles :
0,99999... n'est pas élément de [0 ; 1[.
Horreur