Théorème de Pythagore : comment l'aborder en classe ?

Je continue dans ce fil de discussion, même si ce n'est pas tout à fait le même sujet.
Je réfléchis actuellement à comment je vais aborder la réciproque de Pythagore (sachant qu'ils auront vu le théorème direct 2 mois avant). Je cherche quelque chose d'efficace et pas trop guidé (donc pas une activité géogébra où on a 1 page de programme de construction). Il y a cette activité issue du Transmath :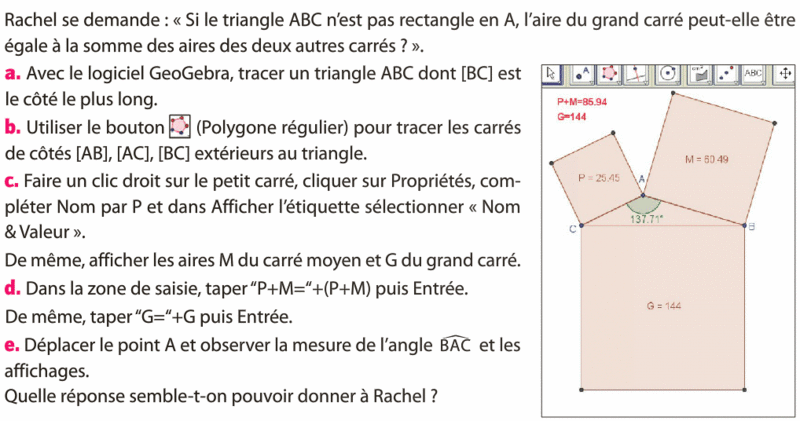

J'avais aussi vu une activité consistant à faire découper aux élèves des carrés en papier dont les côtés seraient les entiers de 1 à 10 et ensuite de disposer 3 carrés pour former un triangle (avec rappel sur l'inégalité triangulaire), mais je ne retrouve plus cette activité.

Avez vous une activité sympa à me proposer ? Ou des idées ?

SandyVeg a écrit:
Je réfléchis actuellement à comment je vais aborder la réciproque de Pythagore (sachant qu'ils auront vu le théorème direct 2 mois avant). Je cherche quelque chose d'efficace

Si tu veux de l'efficace, le plus simple est "on suppose a²=b²+c², on construit ABC rectangle en A avec AB = c et AC = b, alors BC²=AB²+AC² = b²+c² = a² donc BC=a donc le triangle ABC est superposable au triangle de côtés a, b et c, qui est donc rectangle d'hypoténuse a ; par conséquent la réciproque du théorème de Pythagore est vraie". Tu proposes une "rédaction-type", en rappelant que pour vérifier une égalité on calcule séparément les deux membres, tu fais cinq-six exercices (un petit tableau à double entrée qui croise "ABC rect en A"/"ABC pas rect en A" avec "BC²=AB²+AC²"/"BC²<>AB²+AC²" permet de voir que c'est Pythagore dans le sens direct qui permet d'affirmer qu'un triangle comme 6-9-10 p.ex n'est pas rectangle) et il te reste 20 minutes dans ta séance pour bosser autre chose.

Parfois il faut savoir aller droit au but.

ycombe a écrit:
soit a un nombre premier. a = p²/q² conduit à a | p, mettons p = a.k. On arrive après simplification à q² = a.k². donc a|q et contradiction. C'est le même raisonnement que pour √2.

Donc tu utilises le lemme d'Euclide,puisque tu passes de a | p² à a | p. C'est hors programme. Autant une justification avec la parité tiens la route pour √2, autant la généralisation "dans le cadre du programme" me semble très compliquée.

ycombe a écrit:
Je présente le calcul du pgcd par la décomposition en facteurs premiers. C'est au programme, dans les commentaires. Je ne sais pas ce que veut dire «ne doit pas être systématisée»: on étudie une notion et on s'en sert ensuite quand le besoin s'en fait sentir, ou alors on ne l'étudie pas.

Pour moi "ne pas être systématisée" signifie simplement qu'on ne peut pas dire "je considère la décomposition en facteur premier d'un entier a". On ne peut pas prouver l'existence (raisonnement par récurrence) ni l'unicité (nécessite le lemme d'Euclide) de cette décomposition sans sortir du cadre du programme.
On utilise cette notion sur des exemples uniquement, sans jamais parler de son unicité.
Plus globalement en arithmétique il est très difficile de prouver quoi que ce soit sans avoir d'abord le quadruplet PGCD/Euclide/Gauss/Théorème fondamental solidement démontré, donc en 3ème ça paraît quand même très tôt pour ce genre de gymnastique.

ben2510 a écrit:

SandyVeg a écrit:
Je réfléchis actuellement à comment je vais aborder la réciproque de Pythagore (sachant qu'ils auront vu le théorème direct 2 mois avant). Je cherche quelque chose d'efficace

Si tu veux de l'efficace, le plus simple est "on suppose a²=b²+c², on construit ABC rectangle en A avec AB = c et AC = b, alors BC²=AB²+AC² = b²+c² = a² donc BC=a donc le triangle ABC est superposable au triangle de côtés a, b et c, qui est donc rectangle d'hypoténuse a ; par conséquent la réciproque du théorème de Pythagore est vraie". Tu proposes une "rédaction-type", en rappelant que pour vérifier une égalité on calcule séparément les deux membres, tu fais cinq-six exercices (un petit tableau à double entrée qui croise "ABC rect en A"/"ABC pas rect en A" avec "BC²=AB²+AC²"/"BC²<>AB²+AC²" permet de voir que c'est Pythagore dans le sens direct qui permet d'affirmer qu'un triangle comme 6-9-10 p.ex n'est pas rectangle) et il te reste 20 minutes dans ta séance pour bosser autre chose.

Parfois il faut savoir aller droit au but.

Loin de moi l'idée de faire le rabat-joie, mais le théorème qui nous dit que si deux triangles ont les mêmes mesures alors ils sont superposables est totalement hors programme, il utilise les espaces affines et les isométries, rien que ça. D'ailleurs il n'est en rien évident instinctivement, dès qu'on passe aux quadrilatères c'est faux. Par contre c'est vrai qu'on le "voit" dès la sixième, et même avant, quand on construit les triangles au compas. Mais l'utiliser dans le cadre d'une démonstration sans le supposer admis est incohérent.

On en revient à la difficulté (l'impossibilité de mon point de vue) de créer un programme cohérent niveau collège si l'on veut conserver toute la rigueur mathématique.
C'est bien pour cela que dans 99% des pays du monde on ne s'encombre pas de tout ça, et qu'au collège la longueur de l'hypoténuse c'est sqrt(a²+b²), le triangle est rectangle si c²=a²+b², et que la rédaction passe à la trappe.

Pour répondre à SandyVeg, je trouve que l'activité proposée avec Geogebra est particulièrement pertinente   :aau:  , on peut d'ailleurs en faire une quasi identique pour le triangle rectangle et le cercle circonscrit.

@Ben : Je ne suis pas emballée par ta façon de faire, je crois que c'est trop différent de ma façon de faire. J'aurais du mal à me l'approprier et donc à le faire passer à mes élèves. Je crois que je vais finalement utiliser l'activité du Transmath.
Merci pour vos réponses !

frand a écrit:

ycombe a écrit:
soit a un nombre premier. a = p²/q² conduit à a | p, mettons p = a.k. On arrive après simplification à q² = a.k². donc a|q et contradiction. C'est le même raisonnement que pour √2.

Donc tu utilises le lemme d'Euclide,puisque tu passes de a | p² à a | p. C'est hors programme. Autant une justification avec la parité tiens la route pour √2, autant la généralisation "dans le cadre du programme" me semble très compliquée.

Ici on peut utiliser la DEFP: dans la décomposition en facteurs premiers d'un carré les puissances des premiers sont paires, donc si a|p² on a au moins a²|p².

Pour moi "ne pas être systématisée" signifie simplement qu'on ne peut pas dire "je considère la décomposition en facteur premier d'un entier a". On ne peut pas prouver l'existence (raisonnement par récurrence) ni l'unicité (nécessite le lemme d'Euclide) de cette décomposition sans sortir du cadre du programme.
On utilise cette notion sur des exemples uniquement, sans jamais parler de son unicité.

On  peut prouver l'existence au collège par une descente infinie: si n est premier c'est fini, sinon n = p.q avec p et q strictement entre 1 et n. On recommence avec p et q jusqu'à ce que tous les nombres soient premiers, ce qui arrivera nécessairement puisqu'on ne peut descendre plus de n fois en profondeur. C'est un argument plus simple que la récurrence.

Pour l'unicité on peut l'admettre en troisième comme on admet l'existence d'une division euclidienne.

La décomposition en facteurs premiers est un outil puissant, qui permet de calculer PGCD (et PPCM) en éclairant la notion, qui permet de simplifier des fractions et des racines. Pourquoi s'en priver? Elle est utilisable pour le PGCD, on peut la replacer pour les racines. Le programme dit qu'on ne la systématise pas, ce qui ne veut pas dire grand chose sinon que savoir l'utiliser systématiquement n'est pas exigible.

Plus globalement en arithmétique il est très difficile de prouver quoi que ce soit sans avoir d'abord le quadruplet PGCD/Euclide/Gauss/Théorème fondamental solidement démontré, donc en 3ème ça paraît quand même très tôt pour ce genre de gymnastique.

La tentation de vouloir donner une construction des mathématiques formellement correcte a conduit à l'aberration des maths modernes. On ne peut pas restreindre le travail à ce qui est prouvable, il est des points sur lesquels on doit dire: la preuve ne peut pas être donnée ici. Ça ne doit pas empêcher de travailler ces notions-là. La DEFP se travaille en début de secondaire dans d'autres pays, cela s'est fait chez nous aussi par le passé, sans poser de problèmes.

Cela fait plaisir de vous lire ycombe.

ycombe a écrit:
Ici on peut utiliser la DEFP: dans la décomposition en facteurs premiers d'un carré les puissances des premiers sont paires, donc si a|p² on a au moins a²|p².

Bien évidemment, puisque quand on a la DEFP on peut tout faire en arithmétique. C'est en effet un outil très puissant, limite marteau de Thor.

ycombe a écrit: Pour l'unicité on peut l'admettre en troisième comme on admet l'existence d'une division euclidienne.  

Dont acte, la démonstration est hors programme. C'est bien là-dessus qu'on essayait de se mettre d'accord, non ?

ycombe a écrit:
La décomposition en facteurs premiers est un outil puissant, qui permet de calculer PGCD (et PPCM) en éclairant la notion, qui permet de simplifier des fractions et des racines. Pourquoi s'en priver?

Il ne faut surtout pas s'en priver, c'est très utile au collège, et ça permet aux élèves de s'améliorer en calcul mental. Je l'utilise sur des exemples dès la 6ème. Par contre l'utiliser pour un entier naturel quelconque, c'est un peu tôt je trouve, notamment car l'unicité de cette décomposition prend alors toute son importance. C'est cette unicité qui va permettre d'affirmer l'unicité de l'écriture p/q avec p et q premiers entre eux pour un rationnels, c'est cette unicité qui va permettre de justifier l’irrationalité de certains radicaux, mais tout ça est abordé au lycée, et le programme de 3ème est déjà chargé. Pourquoi le charger davantage ?