Théorème de Pythagore : comment l'aborder en classe ?

Peut être une façon intéressante d'obtenir l'égalité de Pythagore à partir d'un calcul d'aire ...
Peut être une approche numérique dans un premier temps ...
4*(x*y/2) correspond à la somme des aires des 4 triangles rectangles et (y-x)² correspond à l'aire du petit carré.

gpelletier4 a écrit:Peut être une façon intéressante d'obtenir l'égalité de Pythagore à partir d'un calcul d'aire ...
Peut être une approche numérique dans un premier temps ...
4*(x*y/2) correspond à la somme des aires des 4 triangles rectangles et (y-x)² correspond à l'aire du petit carré.

Très joli. Ne pas oublier de justifier que le grand est un carré (angles complémentaires, tout ça. Le petit est trivial.).

Bonjour à tous, nouveau sur le forum (mais pas néoprof), je lis régulièrement vos discussions avec beaucoup d'intérêt. En ce qui me concerne, après une bonne dizaine d'année au collège avec des 4èmes quasiment tous les ans, j'arrive à peu près à ce type de progression sur ce chapitre :

séance 1 : Séance d'exercices : je donne les formules magiques : sqrt(a²+b²)=h et sqrt(h²-a²)=b. Application immédiate avec la calculatrice sur des dizaines de longueurs dans des triangles rectangles. Concours de vitesse entre élèves. (j'en profite pour revoir les arrondis, les troncatures). Application à des cas concrets.
séance 2 : Séance d'exercices : je donne les formules magiques a²+b²=h² et h²-a²=b². Les élèves comprennent d'eux-mêmes l'utilité de la racine pour trouver une longueur et pas une aire. De nouveau concours de vitesse, pour trouver des aires, des longueurs, déterminer si un triangle est rectangle, toujours à la calculatrice.
séance 3 : Démonstration(s) du théorème. Ma préférée reste celle qui utilise les parallélogrammes. Le découpage/collage, c'est à la maison.   
séances suivantes : formalisation, exos d'applications rédigés...

Intéressant,
La démonstration avec les familles de parallélogrammes tu l'expliques comment ?

pailleauquebec a écrit:Intéressant,
La démonstration avec les familles de parallélogrammes tu l'expliques comment ?

Oups je ne me rappelais plus avoir posté ici, désolé !!!
D'abord je leur montre une animation, par exemple ça : http://therese.eveilleau.pagesperso-orange.fr/pages/truc_mat/pythagor/textes/demos_an.htm
Ensuite on rédige ensemble la démo, généralement ça passe très bien. Et on revoit l'aire des prlg, ce qui n'est pas du luxe.   

Par la duplication du carré dans le Menon de Platon.
http://www.google.fr/url?sa=t&rct=j&q=&esrc=s&source=web&cd=14&cad=rja&uact=8&ved=0CHgQFjAN&url=http%3A%2F%2Fwww.univ-irem.fr%2Freperes%2Farticles%2F78_article_529.pdf&ei=I07IU6DDI4bG0QWiwoCoCw&usg=AFQjCNHJ0qSu5ghkx4akFnrLpjmxRD8bvA&sig2=WW4UOiz1nTox_DlKaG6nQw

Cripure a écrit:Par la duplication du carré dans le Menon de Platon.[b]

Du temps où on avait des horaires décents en grec au collège, je voyais ce texte en fin d'année ; avec une mise en scène appropriée,  les élèves adoraient  

Cripure a écrit:Par la duplication du carré dans le Menon de Platon.
http://www.google.fr/url?sa=t&rct=j&q=&esrc=s&source=web&cd=14&cad=rja&uact=8&ved=0CHgQFjAN&url=http%3A%2F%2Fwww.univ-irem.fr%2Freperes%2Farticles%2F78_article_529.pdf&ei=I07IU6DDI4bG0QWiwoCoCw&usg=AFQjCNHJ0qSu5ghkx4akFnrLpjmxRD8bvA&sig2=WW4UOiz1nTox_DlKaG6nQw

On est quand même dans un cas très particulier, le triangle rectangle isocèle, avec une relation du type c²=2a². La généraliser au triangle rectangle scalène ne va pas de soi, mais c'est intéressant comme idée.

Je propose, je laisse les spécialistes décider de la pertinence

Cripure a écrit:Par la duplication du carré dans le Menon de Platon.
http://www.google.fr/url?sa=t&rct=j&q=&esrc=s&source=web&cd=14&cad=rja&uact=8&ved=0CHgQFjAN&url=http%3A%2F%2Fwww.univ-irem.fr%2Freperes%2Farticles%2F78_article_529.pdf&ei=I07IU6DDI4bG0QWiwoCoCw&usg=AFQjCNHJ0qSu5ghkx4akFnrLpjmxRD8bvA&sig2=WW4UOiz1nTox_DlKaG6nQw

Je verrai plutôt ce type d'activité en 3ème, lorsqu'on découvre vraiment la racine carrée.
On reconnaît bien là la patte IREM, des activités aussi intéressantes qu'interminables.  :lol: 
Ah là là mes trois années passées dans ce collège où on utilisait le bouquin "la sixième entre fractions et décimaux" (pour ceux qui connaissent) ... Plus jamais !

frand a écrit:
Je verrai plutôt ce type d'activité en 3ème, lorsqu'on découvre vraiment la racine carrée.

On a vraiment besoin de la racine carrée lorsqu'on étudie les applications du théorème de Pythagore pour calculer une longueur. En placer l'étude l'année suivante fait partie des incohérences des programmes.

ycombe a écrit:

frand a écrit:
Je verrai plutôt ce type d'activité en 3ème, lorsqu'on découvre vraiment la racine carrée.

On a vraiment besoin de la racine carrée lorsqu'on étudie les applications du théorème de Pythagore pour calculer une longueur. En placer l'étude l'année suivante fait partie des incohérences des programmes.

Il me paraît incroyablement compliqué de faire un programme sans incohérences en mathématiques, et si l'on y parvenait, il serait sans aucun doute bien moins simple à assimiler pour l'élève.
L'incohérence sur la racine carrée est minime, en 4ème il faut juste comprendre que lorsqu'on a l'aire d'un carré, on utilise la touche racine carré pour obtenir la longueur d'un côté, ça s'arrête là.

frand a écrit:

ycombe a écrit:

frand a écrit:
Je verrai plutôt ce type d'activité en 3ème, lorsqu'on découvre vraiment la racine carrée.

On a vraiment besoin de la racine carrée lorsqu'on étudie les applications du théorème de Pythagore pour calculer une longueur. En placer l'étude l'année suivante fait partie des incohérences des programmes.

Il me paraît incroyablement compliqué de faire un programme sans incohérences en mathématiques, et si l'on y parvenait, il serait sans aucun doute bien moins simple à assimiler pour l'élève.
L'incohérence sur la racine carrée est minime, en 4ème il faut juste comprendre que lorsqu'on a l'aire d'un carré, on utilise la touche racine carré pour obtenir la longueur d'un côté, ça s'arrête là.

Les élèves s'habituent, une fois de plus, à utiliser la calculatrice dès qu'un calcul est à faire. Ils s'habituent à utiliser une notion sans qu'on la leur ait expliquée, et ils s'habituent à confondre allègrement valeur exacte et valeur approchée puisque dans la plupart des cas les racines sont irrationnelles. Ils s'habituent à ce que les cours de mathématiques se résument à une série de boites noires, tu appuies sur le bouton et tu as la réponse. Ils confondent allègrement les calculs de longueurs et les vérifications de rectitude.

On pourrait enseigner l'extraction de racine entière à la main en tant qu'algorithme −la racine entière est utile en arithmétique (crible d'Erathostène, liste des diviseurs d'en nombre, test basique de primalité)− puis la racine exacte avant d'enseigner Pythagore.

frand a écrit:

Il me paraît incroyablement compliqué de faire un programme sans incohérences en mathématiques, et si l'on y parvenait, il serait sans aucun doute bien moins simple à assimiler pour l'élève.

N’exagérons rien !
Par contre les programmes actuels ont tendance à étaler les notions sur plusieurs années successives (p.ex pour la racine carrée la fait de multiplier par une qté conjuguée pour éliminer un radical au dénominateur n'est au programme qu'en 1S), ce qui n'est pas nécessairement une bonne chose, comme (autre exemple) les fractions au primaire et au collège.
Il me semble avoir lu dans je ne sais plus quelle étude que dans d'autres systèmes, les notions étaient plus ramassées dans les cursus, avec des résultats plus convaincants en terme d'apprentissage des élèves.
Avec le système actuel, tout est toujours "en cours d'acquisition" et rien n'est jamais vraiment fixé.

frand a écrit:
L'incohérence sur la racine carrée est minime, en 4ème il faut juste comprendre que lorsqu'on a l'aire d'un carré, on utilise la touche racine carré pour obtenir la longueur d'un côté, ça s'arrête là.

Je ne suis pas d'accord.
La notion de racine carrée participe de la construction de la notion de nombre, en l’occurrence de nombres irrationnels.
L'essentiel n'est pas de savoir appuyer sur un bouton, mais de savoir qu'un côté "ne tombe pas juste", même en mettant beaucoup de chiffres après le virgule...

[quote="ycombe"][quote="frand"]

ycombe a écrit:
Les élèves s'habituent, une fois de plus, à utiliser la calculatrice dès qu'un calcul est à faire. Ils s'habituent à utiliser une notion sans qu'on la leur ait expliquée, et ils s'habituent à confondre allègrement valeur exacte et valeur approchée puisque dans la plupart des cas les racines sont irrationnelles. Ils s'habituent à ce que les cours de mathématiques se résument à une série de boites noires, tu appuies sur le bouton et tu as la réponse. Ils confondent allègrement les calculs de longueurs et les vérifications de rectitude.

On pourrait enseigner l'extraction de racine entière à la main en tant qu'algorithme −la racine  entière est utile en arithmétique (crible d'Erathostène, liste des diviseurs d'en nombre, test basique de primalité)− puis la racine exacte avant d'enseigner Pythagore.

Je te rejoins sur le caractère dommageable de ne plus enseigner l'algorithme qui permet d'approximer les racines carrés, même si l'on peut tout à fait, en calcul mental, demander aux élèves de donner des valeurs approchées au dixième de racines carrés. Ou faire un petit DM/ une séance sur la façon dont la calculatrice parvient à nous afficher ce nombre.
Je te rejoins aussi sur l'importance de la différence valeur exacte/valeur approchée. Reste que cette différence peut être assimilée sans aller plus avant sur cette notion de racine carrée.
Je te rejoins enfin sur l'importance de ne pas confondre calcul de longueur et vérification de rectitude. Reste que cette confusion ne viens pas de la méconnaissance de l’irrationalité de certaines racines carrées.

Je précise que pour moi, l'intérêt était la conversation platonicienne autour des mathématiques. Pour une fois que je prêche pour la transversalité

frand a écrit: Reste que cette confusion ne viens pas de la méconnaissance de l’irrationalité de certaines racines carrées.

Non, elle provient −aussi− de la méconnaissance de la racine carrée. Le calcul de la longueur manquante par Pythagore, dans l'état actuel du programme, c'est juste sortir sa calculatrice et appuyer sur un bouton. La vérification du la rectitude, c'est aussi sortir sa calculatrice et appuyer sur un bouton. Ce n'est pas le même bouton, mais à la base il y a la même relation. Les boutons de la calculatrice rendent opaques les calculs, d'autant plus si les calculs n'ont pas été étudiés préalablement.

Cripure a écrit:Je précise que pour moi, l'intérêt était la conversation platonicienne autour des mathématiques. Pour une fois que je prêche pour la transversalité

Le dialogue sur le doublement du carré me sert en seconde lorsque nous démontrons l'irrationalité de racine (2).
Et à ma connaissance il reste un classique en terminale, en Philosophie !

ben2510 a écrit:
Je ne suis pas d'accord.
La notion de racine carrée participe de la construction de la notion de nombre, en l’occurrence de nombres irrationnels.
L'essentiel n'est pas de savoir appuyer sur un bouton, mais de savoir qu'un côté "ne tombe pas juste", même en mettant beaucoup de chiffres après le virgule...

Mais quelle explication donnes-tu à tes élèves pour leur expliquer que cette racine n'est pas un rationnel en restant dans le cadre du programme du collège? Tu es bien forcé de l'admettre, non ? C'est un peu léger pour parler de la construction des nombres réels je trouve. Personnellement j'en discute avec eux oralement, notamment le fait qu'ils n'ont pas de fréquence contrairement aux rationnels mais ça s'arrête là.

ycombe a écrit:

frand a écrit: Reste que cette confusion ne viens pas de la méconnaissance de l’irrationalité de certaines racines carrées.

Non, elle provient −aussi− de la méconnaissance de la racine carrée. Le calcul de la longueur manquante par Pythagore, dans l'état actuel du programme, c'est juste sortir sa calculatrice et appuyer sur un bouton. La vérification du la rectitude, c'est aussi sortir sa calculatrice et appuyer sur un bouton. Ce n'est pas le même bouton, mais à la base il y a la même relation. Les boutons de la calculatrice rendent opaques les calculs, d'autant plus si les calculs n'ont pas été étudiés préalablement.

Ben ça doit faire 13 ans que je me coltine des 4èmes chaque rentrée, le théorème de Pythagore je l'ai testé de nombreuses façons, et finalement le plus efficace de mon point de vue c'est d'abord de commencer par bien maîtriser les deux boutons de sa calculatrice justement, pour ensuite basculer à l'écriture des calculs dans les différents cas. Je trouve que mes élèves font nettement moins d'erreurs, y compris dans leurs rédactions, depuis que j'ai décidé de présenter les choses dans cet ordre.

frand a écrit:

ben2510 a écrit:
Je ne suis pas d'accord.
La notion de racine carrée participe de la construction de la notion de nombre, en l’occurrence de nombres irrationnels.
L'essentiel n'est pas de savoir appuyer sur un bouton, mais de savoir qu'un côté "ne tombe pas juste", même en mettant beaucoup de chiffres après le virgule...

Mais quelle explication donnes-tu à tes élèves pour leur expliquer que cette racine n'est pas un rationnel en restant dans le cadre du programme du collège? Tu es bien forcé de l'admettre, non ? C'est un peu léger pour parler de la construction des nombres réels je trouve. Personnellement j'en discute avec eux oralement, notamment le fait qu'ils n'ont pas de fréquence contrairement aux rationnels mais ça s'arrête là.

Bah rien que du classique, avec un raisonnement sur la parité de p et q si on écrit p²/q²=2 avec p/q irréductible.
Mais cela fait huit ans que je suis passé au lycée, et j'ai l'impression que l'enseignement des fractions est devenu assez pitoyable en collège (p.ex en cinquième n'ajouter que des fractions à dénominateur commun évident si j'en crois ce que disent les collègues sur le discours inspectoral....).

Par contre avec des sixièmes j'ai fait des trucs rigolos... un petit compte rendu rapide :
* "Pour demain, construisez-moi un carré d'aire 29 sur papier quadrillé" (le dire très vite, après la sonnerie si possible, et s'enfuir avant que les élèves aient le temps de réfléchir)
* Le lendemain, 3 minutes avant la sonnerie, revenir sur ce travail. Emeute, bien sûr "nan mais mon papa il a dit que c'était pas possible", ou alors des élèves qui ont cherché une valeur approchée de racine(29)...
je regarde un peu ce que les élèves ont fait (rien de bon...), je prends l'air ennuyé, et précises : "oops j'ai oublié de dire que les sommets du carré doivent être sur le quadrillage"

La suite au prochain épisode

frand a écrit:

ben2510 a écrit:
Je ne suis pas d'accord.
La notion de racine carrée participe de la construction de la notion de nombre, en l’occurrence de nombres irrationnels.
L'essentiel n'est pas de savoir appuyer sur un bouton, mais de savoir qu'un côté "ne tombe pas juste", même en mettant beaucoup de chiffres après le virgule...

Mais quelle explication donnes-tu à tes élèves pour leur expliquer que cette racine n'est pas un rationnel en restant dans le cadre du programme du collège? Tu es bien forcé de l'admettre, non ? C'est un peu léger pour parler de la construction des nombres réels je trouve. Personnellement j'en discute avec eux oralement, notamment le fait qu'ils n'ont pas de fréquence contrairement aux rationnels mais ça s'arrête là.

Je l'explique en troisième:
1/ la racine carrée d'un nombre se calcule de proche en proche, un peu comme une division. Je donne la méthode.
2/ la racine carrée d'un entier est un entier ou un nombre non décimal. Preuve par l’absurde: s'il était décimal avec, par exemple, 17 chiffres après la virgule, le carré aurait 34 chiffres et non pas 0.
3/ Les fractions non décimales ont un développement décimal périodique (à partir d'un certain rang). Je fais au tableau 15/7 pour rappeler pourquoi. La réciproque est-elle vraie? Un nombre à virgule périodique peut-il s'écrire comme une fraction? Je donne la méthode, et je glisse au passage que 0,9999999999999… est rigoureusement égal à 1.
4/ Une racine carrée d'un nombre entier non carré peut-elle être périodique? Cela revient à l'écrire comme fraction, qu'on peut prendre irréductible. Prenons √2 comme exemple, et montrons que non. Démonstration classique. √2 est irrationnel. On généralise sans problème à tous les nombres premiers.
5/ Un petit mot, à partir de la décomposition en facteurs premiers (vue pour les PGCD) sur la généralisation du 4/ aux nombres non premiers.

En quatrième je commence par vidéoprojeter un triangle rectangle avec géogébra, les trois carrés construits sur les côtés du triangle puis je demande aux élèves une conjecture sur les aires des trois carrés. Un élève dit que "le plus grand carré à la même aire que les deux plus petits ensembles"

Je demande aux élèves ce qu'ils en pensent puis je projette cette vidéo:



Ensuite on passe à la démonstration du théorème.

ycombe a écrit:
Je l'explique en troisième:
1/ la racine carrée d'un nombre se calcule de proche en proche, un peu comme une division. Je donne la méthode.
2/ la racine carrée d'un entier est un entier ou un nombre non décimal. Preuve par l’absurde: s'il était décimal avec, par exemple, 17 chiffres après la virgule, le carré aurait 34 chiffres et non pas 0.
3/ Les fractions non décimales ont un développement décimal périodique (à partir d'un certain rang). Je fais au tableau 15/7 pour rappeler pourquoi. La réciproque est-elle vraie? Un nombre à virgule périodique peut-il s'écrire comme une fraction? Je donne la méthode, et je glisse au passage que 0,9999999999999… est rigoureusement égal à 1.
4/ Une racine carrée d'un nombre entier non carré peut-elle être périodique? Cela revient à l'écrire comme fraction, qu'on peut prendre irréductible. Prenons √2 comme exemple, et montrons que non. Démonstration classique. √2 est irrationnel. On généralise sans problème à tous les nombres premiers.
5/ Un petit mot, à partir de la décomposition en facteurs premiers (vue pour les PGCD) sur la généralisation du 4/ aux nombres non premiers.

Pour le 2 j'imagine que tu as bien précisé que le carré à 34 chiffres après la virgule car le dernier chiffre du produit ne peut être égal à 0.
Pour le 3 donc tu ne fais pas de démonstration, ni dans un sens ni dans l'autre.
Pour le 4 on utilise des équations diophantiennes du second degré. La généralisation "sans problème", je demande à voir.
Pour le 5 rappelons donc que le programme stipule que la décomposition en facteur premiers ne doit pas être systématisée.
On sort très nettement du cadre du programme mais pourquoi pas, ça reste accessible. Et c'est intéressant pour les élèves. Par contre on est vraiment sur du cours magistral, et ça ne dure pas 5 minutes...

Mais j'en reste au niveau 4ème, comment présentes-tu la racine carrée ?

frand a écrit:

ycombe a écrit:
Je l'explique en troisième:
1/ la racine carrée d'un nombre se calcule de proche en proche, un peu comme une division. Je donne la méthode.
2/ la racine carrée d'un entier est un entier ou un nombre non décimal. Preuve par l’absurde: s'il était décimal avec, par exemple, 17 chiffres après la virgule, le carré aurait 34 chiffres et non pas 0.
3/ Les fractions non décimales ont un développement décimal périodique (à partir d'un certain rang). Je fais au tableau 15/7 pour rappeler pourquoi. La réciproque est-elle vraie? Un nombre à virgule périodique peut-il s'écrire comme une fraction? Je donne la méthode, et je glisse au passage que 0,9999999999999… est rigoureusement égal à 1.
4/ Une racine carrée d'un nombre entier non carré peut-elle être périodique? Cela revient à l'écrire comme fraction, qu'on peut prendre irréductible. Prenons √2 comme exemple, et montrons que non. Démonstration classique. √2 est irrationnel. On généralise sans problème à tous les nombres premiers.
5/ Un petit mot, à partir de la décomposition en facteurs premiers (vue pour les PGCD) sur la généralisation du 4/ aux nombres non premiers.

Pour le 2 j'imagine que tu as bien précisé que le carré à 34 chiffres après la virgule car le dernier chiffre du produit ne peut être égal à 0.

En effet. C'est assez vite fait.

Pour le 3 donc tu ne fais pas de démonstration, ni dans un sens ni dans l'autre.

J'explique sur un exemple, parce qu'en général ils ont oublié la condition sur le reste partiel. Une fois cette condition rappelée, le raisonnement est une démonstration. On ne l'écrit pas formellement (c'est un peu lourd à détailler) mais c'est une démonstration.

Pour l'autre sens la méthode de calcul de la fraction est en soi une démonstration, il me semble. Je prouve l'égalité avec une fraction en donnant la méthode pour trouver cette fraction.

Pour le 4 on utilise des équations diophantiennes du second degré. La généralisation "sans problème", je demande à voir.

soit a un nombre premier. a = p²/q² conduit à a | p, mettons p = a.k. On arrive après simplification à q² = a.k². donc a|q et contradiction. C'est le même raisonnement que pour √2.

Pour le 5 rappelons donc que le programme stipule que la décomposition en facteur premiers ne doit pas être systématisée.
On sort très nettement du cadre du programme mais pourquoi pas, ça reste accessible. Et c'est intéressant pour les élèves. Par contre on est vraiment sur du cours magistral, et ça ne dure pas 5 minutes...

Je présente le calcul du pgcd par la décomposition en facteurs premiers. C'est au programme, dans les commentaires. Je ne sais pas ce que veut dire «ne doit pas être systématisée»: on étudie une notion et on s'en sert ensuite quand le besoin s'en fait sentir, ou alors on ne l'étudie pas.

Je n'ai pas de problème avec le cours magistral. C'est une excellente façon de travailler. Je fais cette série étalée sur plusieurs séances, mixée avec d'autres choses.

Mais j'en reste au niveau 4ème, comment présentes-tu la racine carrée ?

Je n'ai pas de quatrième, mais la présentation que je fais en troisième pourrait très bien se faire en quatrième: racine carrée entière, propriété du reste, algorithme de calcul. Puis plus tard racine carrée exacte, calcul, propriétés. Je démontre la propriété sur √(ab).

Je continue dans ce fil de discussion, même si ce n'est pas tout à fait le même sujet.
Je réfléchis actuellement à comment je vais aborder la réciproque de Pythagore (sachant qu'ils auront vu le théorème direct 2 mois avant). Je cherche quelque chose d'efficace et pas trop guidé (donc pas une activité géogébra où on a 1 page de programme de construction). Il y a cette activité issue du Transmath :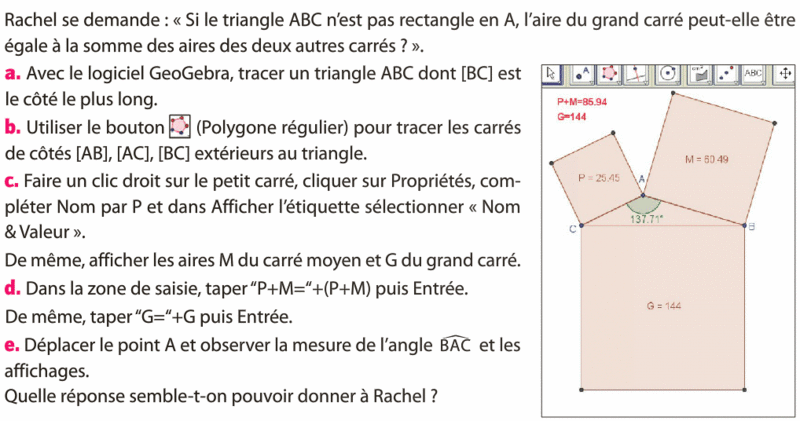

J'avais aussi vu une activité consistant à faire découper aux élèves des carrés en papier dont les côtés seraient les entiers de 1 à 10 et ensuite de disposer 3 carrés pour former un triangle (avec rappel sur l'inégalité triangulaire), mais je ne retrouve plus cette activité.

Avez vous une activité sympa à me proposer ? Ou des idées ?