Page 4 sur 5 •  1, 2, 3, 4, 5
1, 2, 3, 4, 5 
 1, 2, 3, 4, 5
1, 2, 3, 4, 5 
- AndréCNiveau 9
Progression des années 60 (Ardiot) :
https://manuelsanciens.blogspot.fr/2016/06/ardiot-wanauld-budin-calcul-cm1-1963_28.html
- un chiffre au diviseur
- diviseur à 2 chiffres, 1 chiffre au quotient
- diviseur à 2 ou 3 chiffres
- division à quotient décimal
- dividende décimal
- diviseur décimal
- diviseur multiples de 10; 100 ou 1000
- zéro intercalaires au quotient
- quotient plus petit que 1
- diviseur plus petit que 1
- quotient approché
https://manuelsanciens.blogspot.fr/2016/06/ardiot-wanauld-budin-calcul-cm1-1963_28.html
- un chiffre au diviseur
- diviseur à 2 chiffres, 1 chiffre au quotient
- diviseur à 2 ou 3 chiffres
- division à quotient décimal
- dividende décimal
- diviseur décimal
- diviseur multiples de 10; 100 ou 1000
- zéro intercalaires au quotient
- quotient plus petit que 1
- diviseur plus petit que 1
- quotient approché
 ycombeMonarque
ycombeMonarque
Ce n'est pas le pont qui est génant. C'est le discours qui va avec: on ne peut pas diviser un nombre plus pettit par un plus grand.celinesud a écrit:En quoi le pont est-il gênant ?
Et quand on passe à la division décimale, le pont va pouvoir contenir un nombre plus petit que le diviseur, ce qui ne pose pas de problème (chiffre 0 au quotient) mais va à l'encontre de ce qui a été appris précédemment.
On pourrait commencer comme ça…
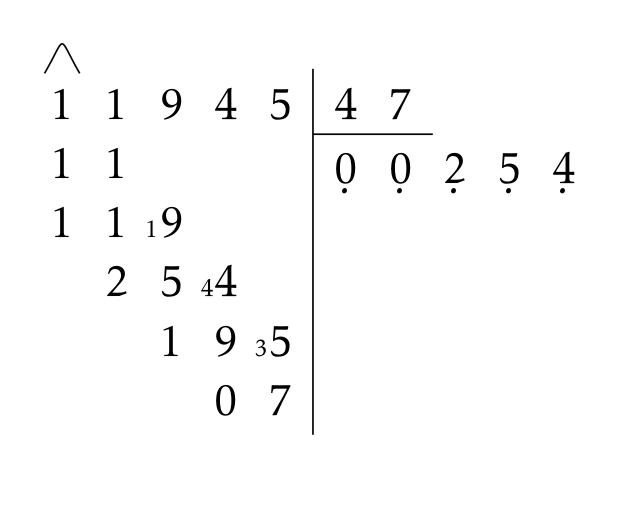
… avant de passer au pont, ou sans passer au pont. Les zéros inutiles sont inutiles, mais ils ne sont pas faux.
_________________
Assurbanipal: "Passant, mange, bois, divertis-toi ; tout le reste n’est rien".
Franck Ramus : "Les sciences de l'éducation à la française se font fort de produire un discours savant sur l'éducation, mais ce serait visiblement trop leur demander que de mettre leur discours à l'épreuve des faits".
 chmarmottineGuide spirituel
chmarmottineGuide spirituel
Je ne pense pas que ce soit enseigner de cette façon.ycombe a écrit:Ce n'est pas le pont qui est génant. C'est le discours qui va avec: on ne peut pas diviser un nombre plus pettit par un plus grand.celinesud a écrit:En quoi le pont est-il gênant ?
 ycombeMonarque
ycombeMonarque
Non, mais c'est souvent ce qu'il reste de cette façon de faire: on ne peut pas commencer avec un nombre plus petit. Alors qu'avec la division décimale, on le fera.celinesud a écrit:Je ne pense pas que ce soit enseigner de cette façon.ycombe a écrit:Ce n'est pas le pont qui est génant. C'est le discours qui va avec: on ne peut pas diviser un nombre plus pettit par un plus grand.celinesud a écrit:En quoi le pont est-il gênant ?
Autant le faire directement.
_________________
Assurbanipal: "Passant, mange, bois, divertis-toi ; tout le reste n’est rien".
Franck Ramus : "Les sciences de l'éducation à la française se font fort de produire un discours savant sur l'éducation, mais ce serait visiblement trop leur demander que de mettre leur discours à l'épreuve des faits".
 AndréCNiveau 9
AndréCNiveau 9
Perso, je ne pose jamais de division de décimaux, je reviens toujours à des divisions d'entiers, ce qui me permet d'expliquer la règle (k x a) / (k x b) = a / b.ycombe a écrit:
En passant, la méthode du pont me laisse perplexe, j'aimerais bien que, comme dans la division longue américaine, on apprenne aux élèves à mettre d'abord des 0. Par exemple pour 11945÷47 on dirait d'abord 1÷47 fait 0 et il reste 1, 11÷47 fait 0 et il reste 11, puis 119÷47 fait 2…
On ne passerait au pont qu'ensuite et on préparerait ainsi la division décimale, dans laquelle il est possible de commencer par un ou plusieurs 0 (1,1945÷47 par exemple).
Ainsi effectuer 1,1945 : 47 revient à poser 11945 : 470000 et comme 11945 < 470000, alors on pose 0 au quotient et on abaisse un zéro au dividende : 119450 : 470000 et ainsi de suite.
 ben2510Expert spécialisé
ben2510Expert spécialisé
Effectuer 1,1945 : 47 revient à poser 11945 : 47, plutôt. Pourquoi ces zéros inutiles ?
_________________
On fait la science avec des faits, comme on fait une maison avec des pierres : mais une accumulation de faits n'est pas plus une science qu'un tas de pierres n'est une maison. Henri Poincaré La notion d'équation différentielle est le pivot de la conception scientifique du monde. Vladimir Arnold
 JPhMMDemi-dieu
JPhMMDemi-dieu
La virgule du dividende pose problème aux élèves ?
Ici, seule la virgule du diviseur leur pose problème, ce qui est un problème "normal".
Ici, seule la virgule du diviseur leur pose problème, ce qui est un problème "normal".
_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
 ycombeMonarque
ycombeMonarque
JPhMM a écrit:La virgule du dividende pose problème aux élèves ?
Ici, seule la virgule du diviseur leur pose problème, ce qui est un problème "normal".
EDIT: Je m'excuse, en fait je répondais à ce message-ci:
ben2510 a écrit:Effectuer 1,1945 : 47 revient à poser 11945 : 47, plutôt. Pourquoi ces zéros inutiles ?
Parce qu'avec la virgule (au dividende), on obtient ça directement.

Pas besoin de passer par des multiplications par 10 000; sans virgule au diviseur, la virgule au quotient « correspond » à celle du dividende et se place au même endroit. On le voit mieux dans la division longue posée à l'américaine puisqu'on y écrit les chiffres du quotient au-dessus de ceux du dividende et que la virgule du quotient se retrouve juste au-dessus de celle du dividende.
Edit: j'ajoute que les règles que je donne pour les décimaux sont les suivantes:
1) on déplace les virgules au diviseur et au dividende d'autant de chiffres vers la droite pour qu'il n'y ait plus de virgule au diviseur.
2) Le pont ne doit pas passer au-dessus de la virgule. On l'arrête à la virgule s'il doit dépasser, et on commence alors par un ou plusieurs zéros.
_________________
Assurbanipal: "Passant, mange, bois, divertis-toi ; tout le reste n’est rien".
Franck Ramus : "Les sciences de l'éducation à la française se font fort de produire un discours savant sur l'éducation, mais ce serait visiblement trop leur demander que de mettre leur discours à l'épreuve des faits".
 AndréCNiveau 9
AndréCNiveau 9
En application de la règle ka/kb = a/b.ben2510 a écrit:Effectuer 1,1945 : 47 revient à poser 11945 : 47, plutôt. Pourquoi ces zéros inutiles ?
Donc 1,1945:47 = (1,1945 x 10000) : (47x10000)
On est ramené à une division de deux entiers, ce que les élèves savent faire.
 AndréCNiveau 9
AndréCNiveau 9
Cela dépend des élèves.JPhMM a écrit:La virgule du dividende pose problème aux élèves ?
 AndréCNiveau 9
AndréCNiveau 9
Je laisse les élèves faire avec la technique qu'ils savent faire. S'ils savent faire comme vous le dites, ils font ainsi.ycombe a écrit:
Pas besoin de passer par des multiplications par 10 000; sans virgule au diviseur, la virgule au quotient « correspond » à celle du dividende et se place au même endroit.
Pour ceux qui n'y arrivent pas, on revient à une division de deux entiers.
C'est l'application de la règle ka/kb=a/bycombe a écrit:
Edit: j'ajoute que les règles que je donne pour les décimaux sont les suivantes:
1) on déplace les virgules au diviseur et au dividende d'autant de chiffres vers la droite pour qu'il n'y ait plus de virgule au diviseur.
Je préfère limiter le nombre de cas particuliers. Plus il y en a et plus c'est difficile à mémoriser. Donc, en déplaçant la virgule, ce problème ne se pose plus. Mais je n'empêche pas les élèves de faire ainsi.ycombe a écrit:
2) Le pont ne doit pas passer au-dessus de la virgule. On l'arrête à la virgule s'il doit dépasser, et on commence alors par un ou plusieurs zéros.
 ycombeMonarque
ycombeMonarque
On doit faire 11945÷470000, le premier nombre étant plus petit que le diviseur comment commences-tu la division ?AndréC a écrit:En application de la règle ka/kb = a/b.ben2510 a écrit:Effectuer 1,1945 : 47 revient à poser 11945 : 47, plutôt. Pourquoi ces zéros inutiles ?
Donc 1,1945:47 = (1,1945 x 10000) : (47x10000)
On est ramené à une division de deux entiers, ce que les élèves savent faire.
_________________
Assurbanipal: "Passant, mange, bois, divertis-toi ; tout le reste n’est rien".
Franck Ramus : "Les sciences de l'éducation à la française se font fort de produire un discours savant sur l'éducation, mais ce serait visiblement trop leur demander que de mettre leur discours à l'épreuve des faits".
 JPhMMDemi-dieu
JPhMMDemi-dieu
Je sais bien, c'est bien comme cela que je le fais, et l'enseigne.ycombe a écrit:JPhMM a écrit:La virgule du dividende pose problème aux élèves ?
Ici, seule la virgule du diviseur leur pose problème, ce qui est un problème "normal".
Parce qu'avec la virgule (au dividende), on obtient ça directement.
_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
 AndréCNiveau 9
AndréCNiveau 9
On ne peut pas prendre 1 chiffre, ni 2, ni 3, ni 4, ni 5 puisque 11945 est plus petit que 470000...
Donc dans 11945 on peut mettre 470000 zéro fois. On place 0 au quotient et on abaisse un zéro.
Donc dans 11945 on peut mettre 470000 zéro fois. On place 0 au quotient et on abaisse un zéro.
 ycombeMonarque
ycombeMonarque
Et on place la virgule à ce zéro. Ça ne fait pas une grande différence avec l'idée de "mettre le pont" en l'arrêtant à la virgule et commencer donc par un zéro, en plaçant la virgule au quotient au même endroit qu'au diviseur (aka quand on abaisse le chiffre des dixièmes, on place la virgule au quotient).AndréC a écrit:On ne peut pas prendre 1 chiffre, ni 2, ni 3, ni 4, ni 5 puisque 11945 est plus petit que 470000...
Donc dans 11945 on peut mettre 470000 zéro fois. On place 0 au quotient et on abaisse un zéro.
D'ailleurs, @AndréC, le lien que tu donnes utilises la même méthode que moi pour les décimaux: on rend le diviseur entier (et lui seul), et on place la virgule au quotient en abaissant les dixièmes. Il me semble que c'est la méthode la plus classique.



_________________
Assurbanipal: "Passant, mange, bois, divertis-toi ; tout le reste n’est rien".
Franck Ramus : "Les sciences de l'éducation à la française se font fort de produire un discours savant sur l'éducation, mais ce serait visiblement trop leur demander que de mettre leur discours à l'épreuve des faits".
 ycombeMonarque
ycombeMonarque
Pour en revenir à mon propos, si on enseignait la division en oubliant le pont et en commençant le quotient par des zéros inutiles, on n'aurait moins de problème pour la division décimale: il suffirait de faire la même chose que pour la division euclidienne en mettant la virgule en abaissant les dixièmes. Le méthode américaine (dite long division) montrée dans la vidéo ci-dessus présente cet avantage sur la notre, en faisant correspondre les rangs du dividende et du quotient.
On pourrait ensuite commencer au premier chiffre qui n'est pas un zéro inutile, en amélioration lorsque la méthode est bien maîtrisée.
On pourrait ensuite commencer au premier chiffre qui n'est pas un zéro inutile, en amélioration lorsque la méthode est bien maîtrisée.
_________________
Assurbanipal: "Passant, mange, bois, divertis-toi ; tout le reste n’est rien".
Franck Ramus : "Les sciences de l'éducation à la française se font fort de produire un discours savant sur l'éducation, mais ce serait visiblement trop leur demander que de mettre leur discours à l'épreuve des faits".
 ycombeMonarque
ycombeMonarque
JPhMM a écrit:Je sais bien, c'est bien comme cela que je le fais, et l'enseigne.ycombe a écrit:JPhMM a écrit:La virgule du dividende pose problème aux élèves ?
Ici, seule la virgule du diviseur leur pose problème, ce qui est un problème "normal".
Parce qu'avec la virgule (au dividende), on obtient ça directement.
Mes excuses, je me suis trompé dans la citation. C'est à @ben2510 que je répondais, voir mon édition du message ci-dessus.
_________________
Assurbanipal: "Passant, mange, bois, divertis-toi ; tout le reste n’est rien".
Franck Ramus : "Les sciences de l'éducation à la française se font fort de produire un discours savant sur l'éducation, mais ce serait visiblement trop leur demander que de mettre leur discours à l'épreuve des faits".
 ben2510Expert spécialisé
ben2510Expert spécialisé
Je suis bien d'accord que diviser un décimal par un entier ne nécessite pas de déplacement de virgule.
Ma proposition se plaçait dans le contexte où on aurait voulu se ramener à une division entière ; disons p.ex qu'on veut 10 CS dans le quotient,
on écrit 11945 = 47 * 254,1489361 + 0,0000033
puis 1,1945 = 47 * 0.02541489361 + 0,00000000033
Pas très utile, tout ça !
Ma proposition se plaçait dans le contexte où on aurait voulu se ramener à une division entière ; disons p.ex qu'on veut 10 CS dans le quotient,
on écrit 11945 = 47 * 254,1489361 + 0,0000033
puis 1,1945 = 47 * 0.02541489361 + 0,00000000033
Pas très utile, tout ça !
_________________
On fait la science avec des faits, comme on fait une maison avec des pierres : mais une accumulation de faits n'est pas plus une science qu'un tas de pierres n'est une maison. Henri Poincaré La notion d'équation différentielle est le pivot de la conception scientifique du monde. Vladimir Arnold
 AndréCNiveau 9
AndréCNiveau 9
C'est bien parce qu'il existe plusieurs façons de faire que je laisse les élèves faire de la façon qui leur est la plus simple.ycombe a écrit:
Et on place la virgule à ce zéro. Ça ne fait pas une grande différence avec l'idée de "mettre le pont" en l'arrêtant à la virgule et commencer donc par un zéro, en plaçant la virgule au quotient au même endroit qu'au diviseur (aka quand on abaisse le chiffre des dixièmes, on place la virgule au quotient).
D'ailleurs, @AndréC, le lien que tu donnes utilises la même méthode que moi pour les décimaux: on rend le diviseur entier (et lui seul), et on place la virgule au quotient en abaissant les dixièmes. Il me semble que c'est la méthode la plus classique.
Je reviens à une division d'entier uniquement pour les élèves pour lesquels cela leur est plus facile à faire..
Quant au classicisme des méthodes, d'après ce que j'ai pu lire sur le net lorsque j'ai cherché les méthodes de l'école des années 60, elle n'est pas plus classique que les autres, il y a eu différentes techniques expliquées selon les périodes.
Au 17e siècle, on faisait différemment.
 ycombeMonarque
ycombeMonarque
Quand je dis classique, je veux dire enseignée en classe, plutôt depuis la 3e république donc.
La méthode de division que j'indique dans le poly se trouve déjà dans un livre d'arithmétique de 1852 (voir ici §53 p 33: http://gallica.bnf.fr/ark:/12148/bpt6k921550v/f43.image.r=Cirode%20arithm%C3%A9tique).
La méthode de division que j'indique dans le poly se trouve déjà dans un livre d'arithmétique de 1852 (voir ici §53 p 33: http://gallica.bnf.fr/ark:/12148/bpt6k921550v/f43.image.r=Cirode%20arithm%C3%A9tique).
_________________
Assurbanipal: "Passant, mange, bois, divertis-toi ; tout le reste n’est rien".
Franck Ramus : "Les sciences de l'éducation à la française se font fort de produire un discours savant sur l'éducation, mais ce serait visiblement trop leur demander que de mettre leur discours à l'épreuve des faits".
 AndréCNiveau 9
AndréCNiveau 9
Division à la française au 17e siècle :http://jean-luc.bregeon.pagesperso-orange.fr/Page%200-3.htm
Elle n'était pas posée avec une potence !
Elle n'était pas posée avec une potence !
 ycombeMonarque
ycombeMonarque
Il me semble qu'il s'agit de la méthode Galley, abandonnée à la révolution au profit de celle en potence.AndréC a écrit:Division à la française au 17e siècle :http://jean-luc.bregeon.pagesperso-orange.fr/Page%200-3.htm
Elle n'était pas posée avec une potence !
http://www-irem.ujf-grenoble.fr/revues/revue_n/fic/57/57n4.pdf
http://www-irem.ujf-grenoble.fr/spip/squelettes/fic_N.php?num=58&rang=5
_________________
Assurbanipal: "Passant, mange, bois, divertis-toi ; tout le reste n’est rien".
Franck Ramus : "Les sciences de l'éducation à la française se font fort de produire un discours savant sur l'éducation, mais ce serait visiblement trop leur demander que de mettre leur discours à l'épreuve des faits".
 AndréCNiveau 9
AndréCNiveau 9
Votre façon de faire était celle expliquée par Guy Brousseau dans ses leçons de pédagogie :Volubilys a écrit:Désolée d'être une si mauvaise maîtresse.

http://guy-brousseau.com/wp-content/uploads/2012/10/77-6-li%C3%A9.pdf.
 AndréCNiveau 9
AndréCNiveau 9
Autre technique lorsque le dividende est décimal, faire comme s'il était entier...puis placer la virgule (Vitte 1924)
http://gallica.bnf.fr/ark:/12148/bpt6k9480759/f74.item.r=arithmétique%20%20cours%20élémentaire.zoom
http://gallica.bnf.fr/ark:/12148/bpt6k9480759/f74.item.r=arithmétique%20%20cours%20élémentaire.zoom
 ycombeMonarque
ycombeMonarque
AndréC a écrit:Votre façon de faire était celle expliquée par Guy Brousseau dans ses leçons de pédagogie :Volubilys a écrit:Désolée d'être une si mauvaise maîtresse.

http://guy-brousseau.com/wp-content/uploads/2012/10/77-6-li%C3%A9.pdf.

No comment.
_________________
Assurbanipal: "Passant, mange, bois, divertis-toi ; tout le reste n’est rien".
Franck Ramus : "Les sciences de l'éducation à la française se font fort de produire un discours savant sur l'éducation, mais ce serait visiblement trop leur demander que de mettre leur discours à l'épreuve des faits".
Page 4 sur 5 •  1, 2, 3, 4, 5
1, 2, 3, 4, 5 
 1, 2, 3, 4, 5
1, 2, 3, 4, 5 
- Division par deux du montant de la bourse au mérite
- Contractuel sur deux établissements dans deux communes non-limitrophes : à quoi ai-je droit ?
- Peut-on passer deux CAPES ou agrèg' dans deux matières différentes ?
- Le Point souligne le "deux poids, deux mesures du gouvernement" : les professeurs ignorés !
- Que faire quand on a deux fois deux heures une classe pénible ?
Permission de ce forum:
Vous ne pouvez pas répondre aux sujets dans ce forum


