Re: Le naufrage sans fin en mathématiques. Note d’alerte du CSEN

par lene75 Sam 27 Jan 2024 - 0:17

jaybe a écrit:Je ne partage pas la formulation "piège/piégeur". Les énoncés que je qualifie ainsi sont ceux dans lesquels la part d'implicite rend non formalisable la résolution du problème (ou disons, la rend sujette à discussion/interprétation). Ici, il est juste question de montrer que la représentation première du problème n'est pas la bonne, et de motiver l'utilisation du cadre littéral comme pouvant apporter la réponse à toute personne qui accepte de travailler dans ce cadre.

On parle de PE, donc d'enseignement primaire. À ma connaissance la notation littérale n'est pas introduite en primaire. Il faut donc résoudre le problème sans. Ça me paraît être le deal de base en primaire.

par jaybe Sam 27 Jan 2024 - 0:24

lene75 a écrit:

jaybe a écrit:Je ne partage pas la formulation "piège/piégeur". Les énoncés que je qualifie ainsi sont ceux dans lesquels la part d'implicite rend non formalisable la résolution du problème (ou disons, la rend sujette à discussion/interprétation). Ici, il est juste question de montrer que la représentation première du problème n'est pas la bonne, et de motiver l'utilisation du cadre littéral comme pouvant apporter la réponse à toute personne qui accepte de travailler dans ce cadre.

On parle de PE, donc d'enseignement primaire. À ma connaissance la notation littérale n'est pas introduite en primaire. Il faut donc résoudre le problème sans. Ça me paraît être le deal de base en primaire.

Verdurette évoque une constellation, aussi je ne m'arrête pas à ce qui sera enseigné devant les élèves du primaire. L'enseignement du calcul littéral se prépare avec des activités dépourvues de lettres (par exemple, des raisonnements sur des images) qui font apparaître une structure de résolution qui sera plus tard mobilisée avec les inconnues ; cela peut et doit être abordé avant le cycle 4.

par Mathador Sam 27 Jan 2024 - 1:21

Nicétas a écrit:J'aurais fait ça, de mon côté : soit x le prix de l'étui et y le prix de la tablette

on sait que x + y = 240
donc x = 240 - y
or y = x + 200
donc x = 240 - (x + 200)
donc x = 240 - x + (-200)
donc 2x = 40
donc x = 20

voilà voilà je suis curieux d'avoir vos avis de professeurs de maths sur mes réflexes...

Si je veux faire du mal aux mouches, je dirais que ta preuve n'est pas complète puisque tu n'as ni raisonné par équivalence ni vérifié la solution.
Pour le reste, tu as modélisé le problème par un système de 2 équations à 2 inconnues (sans vraiment expliciter ce système). Cela fonctionne, mais je préfère de mon côté limiter le nombre d'inconnues, et directement dire que la tablette coûte 200+x plutôt que de poser y. Cela revient à anticiper une résolution par substitution du système auquel tu t'es ramené.

par ylm Sam 27 Jan 2024 - 1:36

Nicétas a écrit:J'aurais fait ça, de mon côté : soit x le prix de l'étui et y le prix de la tablette

on sait que x + y = 240
donc x = 240 - y
or y = x + 200
donc x = 240 - (x + 200)
donc x = 240 - x + (-200)
donc 2x = 40
donc x = 20

voilà voilà je suis curieux d'avoir vos avis de professeurs de maths sur mes réflexes...

Le grand défaut des matheux : mettre le truc en équations alors que ça ne sert à rien.

par Aperçu par hasard Sam 27 Jan 2024 - 1:51

ylm a écrit:

Nicétas a écrit:J'aurais fait ça, de mon côté : soit x le prix de l'étui et y le prix de la tablette

on sait que x + y = 240
donc x = 240 - y
or y = x + 200
donc x = 240 - (x + 200)
donc x = 240 - x + (-200)
donc 2x = 40
donc x = 20

voilà voilà je suis curieux d'avoir vos avis de professeurs de maths sur mes réflexes...

Le grand défaut des matheux : mettre le truc en équations alors que ça ne sert à rien.

Ah. J'ai fait un raisonnement pourri mais je ne l'ai pas mis en équations. Ça me rajoute des points? Le naufrage sans fin en mathématiques. Note d’alerte du CSEN - Page 27 2314601941

Le naufrage sans fin en mathématiques. Note d’alerte du CSEN - Page 27 2314601941

par jaybe Sam 27 Jan 2024 - 12:48

Comme le nom n'est pas déjà apparu dans la discussion, un certain nombre de considérations développées ici se placent dans l'approche "Early Algebra" (qui à ma connaissance reste peu connue en France, alors que de l'autre côté de l'Atlantique cela semble bien mieux étudié et compris). Les curieux pourront consulter cet article qui est de la très bonne didactique : les auteurs exposent leur constat, ce qu'ils ont voulu faire, où cela les a menés ; cela se lit bien, c'est placé dans le contexte historique, et les controverses et points de débats ne sont pas éludés (d'ailleurs, lorsque j'ai écrit plus haut que l'entrée dans la lettre pouvait et devait être préparée : elle peut l'être au primaire, les élèves ainsi que les professeurs disposent de tout ce qu'il faut comme études pour en être convaincu sans l'ombre d'un doute aujourd'hui ; le fait qu'elle doive ou non l'être est très bien discuté dans ce travail).

par Manu7 Sam 27 Jan 2024 - 13:43

Prezbo a écrit:

Lowpow29 a écrit:Au moins ça permet de tester les compétences pédagogiques de ceux qui trouvent la réponse

- si la tablette coûte 200€ et l'étui 40€, combien la tablette coute-t-elle de plus que l'étui ? Là j'imagine que la plupart fera 200-40=160 et verra que cela invalide leur première intuition puisqu'on voit que la tablette ne coûte que 160€ de plus que l'étui dans ce cas

Personnellement je comprends que ce soit contre-intuitif pour les gens et ça me semble plus facile à comprendre en décomposant les "prix de..." :
- prix de la tablette = combien ? Prix de l'étui + 200€
- Donc prix des deux = prix de l'étui + prix de la tablette = prix de l'étui + prix de l'étui + 200€
Donc 240€ = 200€ + 2 fois le prix de l'étui
Etc

Les problèmes de maths c'est souvent aussi une question de formulation et là c'est fait exprès pour d'abord induire en erreur...

Mais pourquoi deux étuis ? Il n'y en a qu'un.

Que certains tombent dans le piège ne me choque pas forcément. D'ailleurs, je ne suis pas adepte de cette pédagogie du piège, qui consiste essentiellement à embrouiller des apprenants déjà fragiles sous prétexte de les faire réfléchir.

Que certains ne comprennent toujours pas après explication ne me surprend pas, mais montre l'ampleur du problème : du fait des mode de sélection et d'orientation, certains PE qui étaient en difficulté en maths probablement depuis le primaire restent en difficulté en maths une fois PE.

Dans ma génération (plus de 50 ans), les PE qui avaient des difficultés en maths sont passées par le bac A1, et quand j'échange avec eux, je pense qu'ils ont des bases très solides pour enseigner en primaire. Je pense même que leurs bases sont plus solides que les jeunes PE qui n'étaient pas en difficultés au lycée, sauf qu'entre temps, on a largement favorisé la filière sans maths avec les bac L puis carrément la fin des maths après la seconde.

par beaverforever Sam 27 Jan 2024 - 14:10

chmarmottine a écrit:Ce problème piégeux est connu et on le retrouve sous diverses versions. Je suis prof de maths, je sens le piège venir mais si je vais vite, j'y tombe dedans ....
De plus, je trouve que les explications à rallonge du type "prix de l'étui + prix de " .... compliquent les choses et mon cerveau capte plus vite avec des x ... mon cerveau est sans doute trop déformé ...

Je ne vois pas l'intérêt de ce type de problème à résoudre arithmétiquement, si ce n'est pour apprendre à se méfier des pièges. Je vois plus son intérêt dans l'apprentissage du calcul littéral et des équations.

Ma fille a eu ce type de problème en éval en 6e l'an dernier .... elle est tombée dans le piège ... je ne vois pas trop ce que j'aurais pu en tirer comme conclusion.
C'était un exercice au milieu de plein d'autres, elle a dû lire une fois ou deux et n'a pas cherché plus loin ...

Alors ce problème et ses variantes font partie d'un test psychométrique : le test de réflexion cognitive. C'est un test simple d'une dizaine de questions qui cherche à mesurer la capacité d'un individu à inhiber sa réponse instinctive et activer pertinemment sa pensée méthodique. Les données montrent que les humains (même avec un haut niveau scolaire) sont globalement mauvais, mais qu'une minorité est significativement et durablement meilleure.

Ce test fait partie d'une réflexion plus large sur les biais cognitifs et sur comment les individus se trompent dans leurs raisonnements.

L'autre idée sous-jacente derrière ce test est qu'il est peut-être possible de former les individus à améliorer leur système inhibiteur, celui qui va bloquer la réponse intuitive en détectant les indices d'une erreur probable.

D'où, sans doute, son utilisation dans la partie mathématique des tests nationaux, car connaître la proportion d'élèves intuitifs et inhibiteurs est une information intéressante.

Je ne suis pas certain qu'il soit pertinent de l'utiliser comme un exercice de mathématique sauf à vouloir en faire un support pour réfléchir sur l'inhibition cognitive.

par nicole 86 Sam 27 Jan 2024 - 14:51

beaverforever a écrit:

chmarmottine a écrit:Ce problème piégeux est connu et on le retrouve sous diverses versions. Je suis prof de maths, je sens le piège venir mais si je vais vite, j'y tombe dedans ....
De plus, je trouve que les explications à rallonge du type "prix de l'étui + prix de " .... compliquent les choses et mon cerveau capte plus vite avec des x ... mon cerveau est sans doute trop déformé ...

Je ne vois pas l'intérêt de ce type de problème à résoudre arithmétiquement, si ce n'est pour apprendre à se méfier des pièges. Je vois plus son intérêt dans l'apprentissage du calcul littéral et des équations.

Ma fille a eu ce type de problème en éval en 6e l'an dernier .... elle est tombée dans le piège ... je ne vois pas trop ce que j'aurais pu en tirer comme conclusion.
C'était un exercice au milieu de plein d'autres, elle a dû lire une fois ou deux et n'a pas cherché plus loin ...

Alors ce problème et ses variantes font partie d'un test psychométrique : le test de réflexion cognitive. C'est un test simple d'une dizaine de questions qui cherche à mesurer la capacité d'un individu à inhiber sa réponse instinctive et activer pertinemment sa pensée méthodique. Les données montrent que les humains (même avec un haut niveau scolaire) sont globalement mauvais, mais qu'une minorité est significativement et durablement meilleure.

Ce test fait partie d'une réflexion plus large sur les biais cognitifs et sur comment les individus se trompent dans leurs raisonnements.

L'autre idée sous-jacente derrière ce test est qu'il est peut-être possible de former les individus à améliorer leur système inhibiteur, celui qui va bloquer la réponse intuitive en détectant les indices d'une erreur probable.

D'où, sans doute, son utilisation dans la partie mathématique des tests nationaux, car connaître la proportion d'élèves intuitifs et inhibiteurs est une information intéressante.
Je ne suis pas certain qu'il soit pertinent de l'utiliser comme un exercice de mathématique sauf à vouloir en faire un support pour réfléchir sur l'inhibition cognitive.

Merci pour cette approche qui ne m'est pas familière.
Je veux bien reconnaître que le choix des valeurs numériques peut le faire classer parmi les pièges. Cependant cet exercice fait partie de la catégorie des partages inégaux, un grand classique qu'on peut résoudre par le raisonnement qu'on appelait autrefois arithmétique et qu'on trouve dans la littérature mathématique ancienne (les héritages et autres) et qui, sur le plan pédagogique, préparent à la mise en équation des problèmes.

par Prezbo Sam 27 Jan 2024 - 14:55

beaverforever a écrit:

chmarmottine a écrit:Ce problème piégeux est connu et on le retrouve sous diverses versions. Je suis prof de maths, je sens le piège venir mais si je vais vite, j'y tombe dedans ....
De plus, je trouve que les explications à rallonge du type "prix de l'étui + prix de " .... compliquent les choses et mon cerveau capte plus vite avec des x ... mon cerveau est sans doute trop déformé ...

Je ne vois pas l'intérêt de ce type de problème à résoudre arithmétiquement, si ce n'est pour apprendre à se méfier des pièges. Je vois plus son intérêt dans l'apprentissage du calcul littéral et des équations.

Ma fille a eu ce type de problème en éval en 6e l'an dernier .... elle est tombée dans le piège ... je ne vois pas trop ce que j'aurais pu en tirer comme conclusion.
C'était un exercice au milieu de plein d'autres, elle a dû lire une fois ou deux et n'a pas cherché plus loin ...

Alors ce problème et ses variantes font partie d'un test psychométrique : le test de réflexion cognitive. C'est un test simple d'une dizaine de questions qui cherche à mesurer la capacité d'un individu à inhiber sa réponse instinctive et activer pertinemment sa pensée méthodique. Les données montrent que les humains (même avec un haut niveau scolaire) sont globalement mauvais, mais qu'une minorité est significativement et durablement meilleure.

Ce test fait partie d'une réflexion plus large sur les biais cognitifs et sur comment les individus se trompent dans leurs raisonnements.

L'autre idée sous-jacente derrière ce test est qu'il est peut-être possible de former les individus à améliorer leur système inhibiteur, celui qui va bloquer la réponse intuitive en détectant les indices d'une erreur probable.

D'où, sans doute, son utilisation dans la partie mathématique des tests nationaux, car connaître la proportion d'élèves intuitifs et inhibiteurs est une information intéressante.

Je ne suis pas certain qu'il soit pertinent de l'utiliser comme un exercice de mathématique sauf à vouloir en faire un support pour réfléchir sur l'inhibition cognitive.

Je reste sur ma position : c'est sans doute très intéressant, mais désormais bien loin des préoccupations d'un enseignant du secondaire, qui constate que la moindre exigence de calcul/méthode/rédaction/respect des notations semble d'un niveau de difficulté effarant pour de trop nombreux élèves. Les erreurs dues à une mauvaise interprétation d'un énoncé ou une réponse intuitive trop rapide sont désormais très minoritaires parmi celles auxquelles nous sommes confrontées.

par Nicétas Sam 27 Jan 2024 - 15:27

Mathador a écrit:

Nicétas a écrit:J'aurais fait ça, de mon côté : soit x le prix de l'étui et y le prix de la tablette

on sait que x + y = 240
donc x = 240 - y
or y = x + 200
donc x = 240 - (x + 200)
donc x = 240 - x + (-200)
donc 2x = 40
donc x = 20

voilà voilà je suis curieux d'avoir vos avis de professeurs de maths sur mes réflexes...

Si je veux faire du mal aux mouches, je dirais que ta preuve n'est pas complète puisque tu n'as ni raisonné par équivalence ni vérifié la solution.
Pour le reste, tu as modélisé le problème par un système de 2 équations à 2 inconnues (sans vraiment expliciter ce système). Cela fonctionne, mais je préfère de mon côté limiter le nombre d'inconnues, et directement dire que la tablette coûte 200+x plutôt que de poser y. Cela revient à anticiper une résolution par substitution du système auquel tu t'es ramené.

Ah mais au contraire, je ne demande qu'à progresser ! J'aimerais tellement trouver le temps de m'y remettre sérieusement. On verra après la thèse...
Pour la vérification, je n'ai pas pris la peine de l'écrire, c'est vrai ; et pour l'équivalence, je dois utiliser ⇔ ?

ylm : le professeur de lettres classiques que je suis prend ta remarque comme un compliment, je ne suis absolument pas matheux !

par Mathador Sam 27 Jan 2024 - 18:31

Nicétas a écrit:Pour la vérification, je n'ai pas pris la peine de l'écrire, c'est vrai ; et pour l'équivalence, je dois utiliser ⇔ ?

Je ne conseille pas l'utilisation du symbole logique.
Je vais achever les pauvres diptères en expliquant pourquoi: A <=> B vaut vrai si un nombre pair de propositions sont vraies parmi A et B.
(A <=> B) <=> C est donc vrai soit si un nombre pair de propositions parmi A et B sont vraies, et C est vraie, soit si un nombre impair de propositions parmi A et B sont vraies, et C est fausse. C'est donc une phrase logique qui est vraie si et seulement si un nombre impair de propositions parmi A, B et C sont vraies.
(A <=> B) <=> C et A <=> (B <=> C) ont donc même table de vérité, et pourraient donc s'écrire A <=> B <=> C, mais ce n'est pas la même table de vérité que « (A <=> B) et (B <=> C) » qui est ce que tu veux dire quand tu raisonnes par équivalence.
Je contourne cette difficulté en écrivant en français « si et seulement si », ou en abrégé « ssi ». Alternativement, il m'arrive aussi d'écrire « On résout: » suivi d'une succession d'équations ou de systèmes, qui sont alors implicitement présentés comme équivalents.

Et quitte à m'en prendre aux mouches, une dernière remarque: même en raisonnant par équivalences, finir par « x=20 » est à éviter, car ce n'est pas à proprement parler une conclusion mais une équation particulièrement facile à résoudre. Il est donc souhaitable soit de conclure en explicitant l'ensemble des solutions (qui, pour x=20, est le singleton {20}), soit de conclure en français si c'est un problème « concret » posé en français.

par Fenrir Sam 27 Jan 2024 - 21:20

Mathador a écrit: soit de conclure en français si c'est un problème « concret » posé en français.

Que j'ai à me battre avec mes élèves pour qu'ils répondent aux question quand ils on modélisé un brin (oui, un petit brin, ce sont des collégiens hein)

par Nicétas Sam 27 Jan 2024 - 21:35

Pour la conclusion, je l'aurais fait en tant qu'élève, je me suis arrêté au prix comme un bon feignant, mais en effet il faut conclure explicitement.
Pour le développement sur l'équivalence, merci beaucoup !

par Moonchild Dim 28 Jan 2024 - 16:05

Ce problème est peut-être artificiel et piégeux, mais l'anecdote rapportée par Verdurette soulève tout de même deux questions :
- Des professeurs des écoles bien formés à l'enseignement des mathématiques ne devraient-ils pas être sensibilisés à ce type de piège classique et donc ne pas tomber dedans aussi massivement ?
- Même si tout le monde peut se faire piéger en répondant trop rapidement, des professeurs des écoles bien formés à l'enseignement des mathématiques ne devraient-ils pas être en mesure de comprendre leur erreur lorsqu'elle est signalée et, surtout, expliquée ?

par dandelion Dim 28 Jan 2024 - 16:36

J’ai posé le problème à mon mari (qui parvient toujours à faire les problèmes de maths de notre fille en maths spé, même s’il doit réfléchir) et il est lui aussi tombé dans le piège. Il a ensuite corrigé son erreur mais comme j’ai fait la moue, il a pu déduire qu’il s’était trompé du fait d’une influence extérieure. Il est objectivement ‘bon en maths’.
Je ne vois pas trop en quoi cet exercice est intéressant en primaire. Je me dis même que c’est le type de problème qui peut faire, à tort, conclure ‘qu’on n’est pas bon en maths’, et renoncer. Il s’agit pour moi d’un exercice de style qui n’a guère d’intérêt, si ce n’est de montrer qu’on est meilleur puisqu’on est au courant du piège.
En primaire, le focus sur les connaissances, la manipulation et la maîtrise de la syntaxe française , d’un minimum de vocabulaire et de rigueur sont a priori suffisants. Les enseignants de primaire n’ont pas besoin d’être des spécialistes en mathématiques, ils ont besoin d’être des spécialistes de l’enseignement des mathématiques aux enfants. Est-ce que faire faire cet exercice aux enseignants de primaire est de nature à aider les enseignants du primaire à enseigner les mathématiques? Je suis sceptique.

par L_Apeiron Dim 28 Jan 2024 - 17:22

Prezbo a écrit:

lene75 a écrit:À mon sens le problème vient ici de l'énoncé et pas des réponses. L'énoncé suggère de passer par un raisonnement concret. Or je n'arrive pas à voir de situation concrète dans laquelle il se poserait. S'il y en a, elles sont vraisemblablement tout à fait exceptionnelles. Le plus probable est qu'il s'agit d'un problème abstrait qui a été traduit a posteriori dans des termes concrets qui lui sont inadaptés, et qu'il faut donc retraduire en des termes abstraits pour le résoudre (les fameux 2 étuis qui ne correspondent à aucune réalité) alors même que l'énoncé suggère le contraire. Je suis sûre qu'il y aurait beaucoup moins d'erreurs si le problème était présenté avec des variables plutôt qu'avec une pseudo situation concrète.

Je m’explique. Si on vous donne les données du problème : une tablette et son étui coûtent 200€, l'étui coûte 40€. Quelle question posez-vous à partir de ces données ? C'est-à-dire, dans la vie réelle, celle où on peut être amené à acheter des tablettes et des étuis, de quelle autre information pourriez-vous avoir besoin ?
Il me semble qu'ici la seule réponse possible est que ce qu'on veut connaître est le prix de la tablette sans l'étui, parce qu'on pourrait vouloir acheter la tablette sans étui ou comparer le prix de la tablette dans ce lot indivisible au prix d'une autre tablette vendue seule : ai-je plutôt intérêt à acheter une autre tablette vendue seule et à acheter l'étui à part ? C'est donc ce que la plupart des gens vont spontanément calculer.

Je n'arrive pas à me représenter de situation dans laquelle on aurait besoin de savoir combien la tablette coûte de plus que l'étui. Il me semble que c'est une information qui n'a aucune utilité.

Dans les vieux manuels de primaire, on trouve ce genre d'exercice : trouver la question qui se pose, ou l'information manquante. Ici l'information qui nous manque, c'est le prix de la tablette, pas combien la tablette coûte de plus que l'étui.

Édit : Pardon, je me suis embrouillée avec les différents messages. Si je ne me trompe pas, l'énoncé initial est : "Une tablette et son étui coûtent 240€. La tablette coûte 200€ de plus que l'étui." C'est encore plus tordu. Vous avez déjà vu un magasin dans lequel on n'affiche pas le prix de l'objet mais on vous dit qu'il coûte 200€ de plus qu'un autre dont on ne connaît pas non plus le prix ? Je ne refais pas tout le message au-dessus, il suffit de transposer : on voit bien ici que l'énoncé ne fait référence à aucune situation concrète vraisemblable, or le fait de l'énoncer en des termes concrets suggère qu'il faudrait pour le résoudre se référer à une situation concrète. Ce que font les gens, qui vont mentalement au magasin, et se plantent donc fatalement.

Oui, c'est bien ça. Du faux concret dans lequel on motive de façon totalement artificielle une mise en équation avec une formulation volontairement piégeuse. C'est un piège classique, et je trouve finalement inintéressant sauf pour faire mousser celui qui pose la colle.

On peut arriver à la même équation avec un problème bien plus naturel. J'achète deux cartouches d'encre et une tablette à 200€. sachant que je paye 240€ au total, quel est le prix d'une cartouche d'encre ?

Je trouve toujours très étrange cette référence au "concret" dans le domaine des mathématiques. Les mathématiques sont par essence le domaine du concept.

Le lien entre le théorème de Thalès est les pyramides est justement ce passage aux concepts géométriques développés pour obtenir leur hauteur. Si on aborde les mathématiques sur le mode "ce type de question ne se pose jamais dans la vie de tous les jours", alors oui, autant tout mettre au fond d'un puits. On sait bien qu'à ce stade "à quoi bon lire du Saint-John Perse" n'est pas loin.

Le principe des questions mathématiques consistent (en partie) à se confronter à un principe de "decouverte". Face au dernier théorème de Fermat (dont l'énoncé date de plus de 400 ans), la réaction immédiate est bien de se dire : "Franchement, cela ne va jamais m'arriver dans ma vie de tous les jours". Ainsi :
"Pour tout entier n plus grand de trois, l'équation x^n+y^n=z^n ne possède pas de solution entière autres que (0,0,1), (1,0,0), (0,1,0)"
ne va jamais empêcher qui que ce soit de dormir... à part Andrew Wiles qui a fini par le démontrer dans les années 2000.

Alors, oui, pour moi, accepter de cheminer à l'intérieur des mathématiques, c'est accepter de se poser des questions "libres et gratuites", c'est entraîner son esprit à vagabonder dans un univers où "on ne sait jamais de quoi l’on parle ni si ce que l’on dit est vrai." (Bertrand Russel). De la même façon, lorsque je lis un roman de vampire, je ne sais pas "vraiment" de quoi on parle et je pense vraiment que ce qui est dit n'est pas vrai, mais je trouve que le Dracula de Bram Stoker est un sacré roman !!

Bref, devant cette question de tablette et d'étui, la difficulté réside dans ce que j'appelle le "pas de côté" : elle fait partie de ces questions où l'intuition brute est insuffisante. Il faut faire un pas de côté dans les mathématiques pour trouver une piste (soit par test/erreur/correction, soit par algébrisation, soit par schématisation, etc).

Tenez, pour la route, en voilà une autre :

"Un homme regarde une photographie et affirme : « Je n’ai point de frère ni de sœur, mais le fils de l'homme sur ce portrait est le fils de mon père. »

De qui cet homme regarde-t-il le portrait ?"

Allez, bon dimanche, et n'oubliez pas :
- L'hypothèse de Riemann
- La conjecture de Goldbach
on en fait quoi ? On les met au fond d'un puits vu qu'elles ne vont jamais être utiles dans la vie de tous les jours....?

par dandelion Dim 28 Jan 2024 - 18:16

Les mathématiques étudiées en primaire sont utiles dans la vie de tous les jours justement. Nous avons des élèves qui ne pourraient pas faire certains métiers manuels faute de connaissances mathématiques suffisantes. Il faut tout de même faire un peu de mathématiques pour faire de la pâtisserie ou de la menuiserie, il en faut aussi pour mesurer les médicaments que l’on administre à ses enfants. Les enseignants de primaire doivent permettre aux enfants d’intégrer certaines notions de façon précisément à les rendre si machinales qu’elles sont intuitives.
Quand un professeur d’anglais se rend compte que ses élèves ont des difficultés en maths, c’est que c’est très visible, et que cela handicape les élèves dans leur quotidien. Et comme j’ai fait un peu de primaire, je sais que ce qui dérange mes élèves ce sont des notions qui devraient être acquises en fin de primaire ou de 6e. Récemment mes élèves de 1e devaient retrouver l’âge de deux personnes, avec mention de deux années, et une mention de l’âge durant l’une des années pour chaque personne, et bien cette question que je pensais facile n’a pas été bien réussie, certains élèves calculant même que les deux personnes avaient vieilli à des vitesses différentes. Il s’agissait d’une soustraction de six années, sur un nombre inférieur à 25 … Entre ça et les coefficients qui changeraient la moyenne parce que tu utilises des chiffres de 1 à 4 plutôt que d’utiliser 0.25 à 1, on a de grands moments de solitude.
Soit on se dit que les enfants sont devenus plus bêtes (on ne peut l’exclure absolument d’ailleurs, il y a peut-être des facteurs environnementaux à prendre en considération), soit on se dit qu’on a manqué quelque chose. Je penche pour la seconde option en priorité et je postule que si on n’a pas appris à calculer des pourcentages ou, pire, qu’on ne sait pas diviser ou multiplier, on aura bien du mal à réussir en mathématiques, y compris si on est un logicien hors pair.

par Invité Dim 28 Jan 2024 - 18:30

Dommage que les diplomé(e)s en maths (j'en suis) soient si peu nombreux à devenir professeurs des écoles. Aimer les maths (oui, aimer) est précieux pour enseigner en primaire. Avoir un bac+10 certainement pas, puisque tout mettre en œuvre pour leur apprendre à comprendre les concepts mathématiques relève d'autres qualités que la maîtrise des maths façon agrégation... mais c'est tout de même dommage que nous n'ayons pas plus de matheux qui enseignent au primaire. Vous verriez que ce n'est pas suffisant pour réussir à faire progresser certains élèves. On ne peut pas à la fois fuir le primaire et accuser les profs du primaire de ne pas faire de miracles en maths. Personnellement au début je préférais enseigner au cycle.3. Quand j'ai eu du cycle 2, j'ai commencé à me rendre compte que ma licence de maths n'allait pas être suffisante pour aider les élèves en difficulté. J'ai beaucoup appris en cherchant comment se passe la construction mentale du nombre, de la quantité, les processus (longs) d'énumération, de dénombrement, ... Je me suis donc auto-formée avec la richesse du cycle 1. Tant qu'on ne se forme pas dans ce sens, on a beau avoir des bac+ en maths, on ne servira pas à grand chose pour être un bon enseignant de primaire. Je pense qu'il faut rester humble et se former aux spécificités du cycle précédent plutôt que de s'en plaindre.

par kyu Dim 28 Jan 2024 - 18:54

Verdurette a écrit:En constellation mathématiques la semaine dernière, pour comprendre comment se sentent les élèves face à la résolution de problèmes. Nous étions une vingtaine.
Une tablette et son étui coûtent 240 euros, la tablette coute 200 euros de plus que l'étui.
Combien coûte l'étui ?

J'ai le regret de dire que j'ai été la seule à trouver la réponse.
Le reste de la troupe a trouvé 40.
Et il a été littéralement impossible de faire comprendre à certains que 1 étui + 1 tablette = 1 étui + 1 étui + 200 = 240 donc 2 étuis = 40
Mais pourquoi deux étuis ? Il n'y en a qu'un.

Ce problème est un exemple typique de la méthode de Singapour.

Un élève formé à cette méthode utilise des schémas en barres pour représenter le problème en prenant le prix de l’étui comme unité de mesure.

Voici un schéma possible :

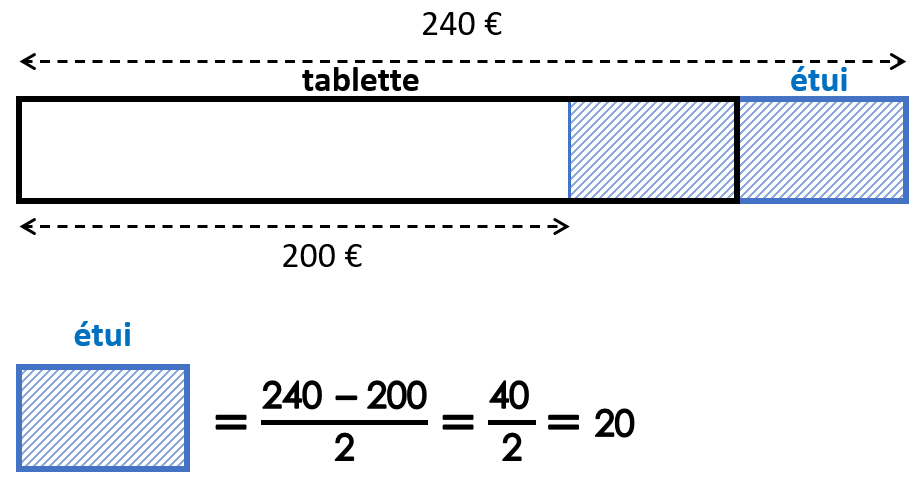
Le naufrage sans fin en mathématiques. Note d’alerte du CSEN - Page 27 Zotui_10

Ce genre de schéma (un classique de la méthode de Singapour) permet de visualiser clairement le problème et de comprendre pourquoi il faut compter deux étuis.

D'autres exemples de résolutions de problèmes par schématisation avec la méthode de Singapour:

Le naufrage sans fin en mathématiques. Note d’alerte du CSEN - Page 27 Mts11

par L_Apeiron Dim 28 Jan 2024 - 19:28

dandelion a écrit:Les mathématiques étudiées en primaire sont utiles dans la vie de tous les jours justement. Nous avons des élèves qui ne pourraient pas faire certains métiers manuels faute de connaissances mathématiques suffisantes. Il faut tout de même faire un peu de mathématiques pour faire de la pâtisserie ou de la menuiserie, il en faut aussi pour mesurer les médicaments que l’on administre à ses enfants. Les enseignants de primaire doivent permettre aux enfants d’intégrer certaines notions de façon précisément à les rendre si machinales qu’elles sont intuitives.
Quand un professeur d’anglais se rend compte que ses élèves ont des difficultés en maths, c’est que c’est très visible, et que cela handicape les élèves dans leur quotidien. Et comme j’ai fait un peu de primaire, je sais que ce qui dérange mes élèves ce sont des notions qui devraient être acquises en fin de primaire ou de 6e. Récemment mes élèves de 1e devaient retrouver l’âge de deux personnes, avec mention de deux années, et une mention de l’âge durant l’une des années pour chaque personne, et bien cette question que je pensais facile n’a pas été bien réussie, certains élèves calculant même que les deux personnes avaient vieilli à des vitesses différentes. Il s’agissait d’une soustraction de six années, sur un nombre inférieur à 25 … Entre ça et les coefficients qui changeraient la moyenne parce que tu utilises des chiffres de 1 à 4 plutôt que d’utiliser 0.25 à 1, on a de grands moments de solitude.
Soit on se dit que les enfants sont devenus plus bêtes (on ne peut l’exclure absolument d’ailleurs, il y a peut-être des facteurs environnementaux à prendre en considération), soit on se dit qu’on a manqué quelque chose. Je penche pour la seconde option en priorité et je postule que si on n’a pas appris à calculer des pourcentages ou, pire, qu’on ne sait pas diviser ou multiplier, on aura bien du mal à réussir en mathématiques, y compris si on est un logicien hors pair.

Il est bien évident que la pratique d'une connaissance, dans la "vie de tous les jours", est nécessaire et doit être pris en compte dans un enseignement ! Il est important d'enseigner le français pour que, si besoin est, nos élèves puissent communiquer/déchiffrer/analyser un texte correctement.

Mon propos consiste juste à dire que la relation de cause à effet "ce n'est pas utile dans la vie de tous les jours donc je ne vois pas l'intérêt de l'enseigner" me paraît être contradictoire avec les mathématiques. La question est essentiellement une question d'objectifs et de "prise de hauteur" : exercer sa pensée en mathématique, en littérature, en physique, histoire, etc m'a toujours paru important (la soif de connaissance chère à Aristote).

Je trouve par exemple que les fichiers Evariste développent une pensée mathématique tout en restant "dans la vie de tous les jours (on parle de livres, de chats, de maisons ; pas de relations d'équivalence, de théorie des schémas ou de métamathématiques).

Concernant la "méthode de Singapour" citée dans un message ci-dessous, je ne comprends pas en quoi il faut lui donner un nom spécifique (à moins que cela soit plus vendeur). Lorsqu'on regarde les textes de certains scientifiques (Al-Kwarizwi, Euler, Descartes, Gauss,...), beaucoup d'entre eux pratiquaient cette "méthode" qui consiste... à modéliser par des schémas.

Ainsi :
1) Par la méthode de Singapour, la courbure de Gauss c'est ça

Le naufrage sans fin en mathématiques. Note d’alerte du CSEN - Page 27 800px-11

2) Par la méthode de Vladivostok, la courbure de Gauss c'est ça

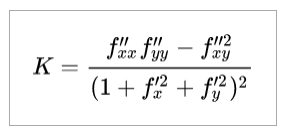
Le naufrage sans fin en mathématiques. Note d’alerte du CSEN - Page 27 Gauss11

par maikreeeesse Dim 28 Jan 2024 - 21:14

Pourtant PE, je ne suis pas tombée dans le piège car j'ai identifié ce type de problème courant. Mais j'ai un souci avec le schéma en barre. Soit l'élève a identifié le problème, comme moi, sait qu'il y a un piège et éventuellement que la différence vaudra 2 étuis (ou tout objet recherché) et alors nul besoin d'un schéma, soit il ne sait pas, il fait son schéma mais ne saura pas que la partie grisée dans le prix de la tablette correspondra au prix d'un étui et donc ne pourra diviser par 2 la différence. Il tâtonnera. Mais là encore il me semble qu'il n' y a pas besoin du schéma. Pour moi il vient après et non avant, comme catégorisation mais pas comme aide à la résolution.

par lene75 Lun 29 Jan 2024 - 1:11

[quote="L_Apeiron"
Mon propos consiste juste à dire que la relation de cause à effet "ce n'est pas utile dans la vie de tous les jours donc je ne vois pas l'intérêt de l'enseigner" me paraît être contradictoire avec les mathématiques. [/quote]

Je crois que personne n'a dit ça. Ce qui est critiqué, c'est le fait de laisser croire qu'on est face à une situation de tous les jours alors que ce n'est pas le cas, et donc de suggérer un type de raisonnement pour la résolution du problème qui n'est pas le raisonnement adéquat dans le but de tromper celui à qui on pose le problème, qu'on aura volontairement mis sur la mauvaise piste pour le piéger.

Il me semble que ça a deux effets pervers :
1) pour les élèves en difficulté (et vraisemblablement les PE pas très calés en maths), les embrouiller en les empêchant d'acquérir d'abord des procédures élémentaires, et les décourager parce qu'ils ont faux alors qu'ils pensaient avoir enfin compris ce qu'il fallait faire. On a le même problème avec les leçons de français où l'exemple qui illustre la leçon est souvent un truc de derrière les fagots qui sème la confusion au lieu d'être le cas le plus classique auquel on s'attendrait pour une première approche de la notion pour des débutants ;
2) pour tous, ça créé des confusions entre les modes de raisonnement qu'il est ensuite difficile de rééduquer.

par verdurin Lun 29 Jan 2024 - 2:44

lene75 a écrit:

L_Apeiron a écrit:
Mon propos consiste juste à dire que la relation de cause à effet "ce n'est pas utile dans la vie de tous les jours donc je ne vois pas l'intérêt de l'enseigner" me paraît être contradictoire avec les mathématiques.

Je crois que personne n'a dit ça. Ce qui est critiqué, c'est le fait de laisser croire qu'on est face à une situation de tous les jours alors que ce n'est pas le cas, et donc de suggérer un type de raisonnement pour la résolution du problème qui n'est pas le raisonnement adéquat dans le but de tromper celui à qui on pose le problème, qu'on aura volontairement mis sur la mauvaise piste pour le piéger.

Il me semble que ça a deux effets pervers :
1) pour les élèves en difficulté (et vraisemblablement les PE pas très calés en maths), les embrouiller en les empêchant d'acquérir d'abord des procédures élémentaires, et les décourager parce qu'ils ont faux alors qu'ils pensaient avoir enfin compris ce qu'il fallait faire. On a le même problème avec les leçons de français où l'exemple qui illustre la leçon est souvent un truc de derrière les fagots qui sème la confusion au lieu d'être le cas le plus classique auquel on s'attendrait pour une première approche de la notion pour des débutants ;
2) pour tous, ça créé des confusions entre les modes de raisonnement qu'il est ensuite difficile de rééduquer.

Je ne cois pas que quiconque puisse croire qu'il est devant une situation « de tous les jours » devant ce problème ( le truc de l’étui ).
C'est au contraire, comme l'ont dit un certain nombre d'intervenants, un moyen pour s'interroger sur nos réponses spontanées.
J'aimerais te voir donner un cours de math.
Et, puisque tu es philosophe, j'aimerais aussi te voir préciser les modes de raisonnements en cause. Et en quoi ils devraient être rééduqués.

par Aperçu par hasard Lun 29 Jan 2024 - 2:59

L_Apeiron a écrit:
Tenez, pour la route, en voilà une autre :

"Un homme regarde une photographie et affirme : « Je n’ai point de frère ni de sœur, mais le fils de l'homme sur ce portrait est le fils de mon père. »

De qui cet homme regarde-t-il le portrait ?"

Bon... j'avoue que cette question me taraude depuis cette après-midi... et comment vais-je m'endormir maintenant sans connaître la réponse? Il regarde un portrait de son père, non? Le naufrage sans fin en mathématiques. Note d’alerte du CSEN - Page 27 2314601941

par Moonchild Lun 29 Jan 2024 - 5:04

dandelion a écrit:J’ai posé le problème à mon mari (qui parvient toujours à faire les problèmes de maths de notre fille en maths spé, même s’il doit réfléchir) et il est lui aussi tombé dans le piège. Il a ensuite corrigé son erreur mais comme j’ai fait la moue, il a pu déduire qu’il s’était trompé du fait d’une influence extérieure. Il est objectivement ‘bon en maths’.
Je ne vois pas trop en quoi cet exercice est intéressant en primaire. Je me dis même que c’est le type de problème qui peut faire, à tort, conclure ‘qu’on n’est pas bon en maths’, et renoncer. Il s’agit pour moi d’un exercice de style qui n’a guère d’intérêt, si ce n’est de montrer qu’on est meilleur puisqu’on est au courant du piège.
En primaire, le focus sur les connaissances, la manipulation et la maîtrise de la syntaxe française , d’un minimum de vocabulaire et de rigueur sont a priori suffisants. Les enseignants de primaire n’ont pas besoin d’être des spécialistes en mathématiques, ils ont besoin d’être des spécialistes de l’enseignement des mathématiques aux enfants. Est-ce que faire faire cet exercice aux enseignants de primaire est de nature à aider les enseignants du primaire à enseigner les mathématiques? Je suis sceptique.

Ton mari a corrigé son erreur et c'est une différence essentielle avec les collègues de constellation de Verdurette qui n'arrivaient apparemment pas à la comprendre quand on leur a expliqué la solution ; ce problème est certes piégeux si on n'est pas concentré, mais il est très loin d'être insurmontable.
Quant à dire si cet exercice est pertinent ou non en primaire, il ne fait sans doute pas partie des priorités mais, s'il est bien présenté avec une méthode de résolution adaptée à des écoliers, il peut sans doute permettre d'introduire un type de raisonnement qui prépare le terrain pour ce qui sera fait au collège (certaines barres du schéma de la méthode de Singapour pouvant par la suite être remplacées par une inconnue désignée par une lettre).
Enfin, faire faire cet exercice à des enseignants de primaire ne les aidera vraisemblablement pas à enseigner les mathématiques s'il s'agit simplement de leur faire percevoir comment se sentent les élèves face à la résolution de problèmes : on reste dans une approche psychologisante alors qu'il serait plutôt nécessaire de fournir à ces enseignants des connaissances qui leur permettrait de traiter correctement ce type de problème (même ce n'est pas l'exercice le plus élémentaire parmi ce qui est traité en classe, il vaut mieux avoir un peu de recul par rapport à ce qu'on enseigne... et quelques billes en réserve) ainsi des techniques pédagogiques éprouvées pour rendre accessible aux élèves la résolution de certaines types de problèmes.

maikreeeesse a écrit:Pourtant PE, je ne suis pas tombée dans le piège car j'ai identifié ce type de problème courant. Mais j'ai un souci avec le schéma en barre. Soit l'élève a identifié le problème, comme moi, sait qu'il y a un piège et éventuellement que la différence vaudra 2 étuis (ou tout objet recherché) et alors nul besoin d'un schéma, soit il ne sait pas, il fait son schéma mais ne saura pas que la partie grisée dans le prix de la tablette correspondra au prix d'un étui et donc ne pourra diviser par 2 la différence. Il tâtonnera. Mais là encore il me semble qu'il n' y a pas besoin du schéma. Pour moi il vient après et non avant, comme catégorisation mais pas comme aide à la résolution.

Pour le schéma en barre, c'est certainement une question d'habitude. L'élève qui a appris à faire sans pour résoudre des problèmes n'en aura pas besoin (il se peut même alors que le schéma le perturbe) à condition qu'il sache reconnaître le piège et identifier le raisonnement ; mais s'il ne sait pas, il tâtonnera et aura beaucoup de mal à trouver la solution tandis qu'un élève habitué aux schémas en barre, même s'il n'est pas spécialement intuitif face aux maths, pourra se rattacher à une méthode de résolution assez efficace et aura plus de chances de trouver la réponse.