Chiffres, nombres, décimaux, questions de terminologie en mathématiques

Mathador a écrit:Si je veux avoir directement le bon résultat, oui, tout comme pour les unités physiques: AB² = AC² + CB² = 16 m² + 9 m² = 25 m² donc AB = 5 m par exemple.
L'alternative est de tout faire en littéral avant l'application numérique, comme on me l'a enseigné en physique en prépa.

On m'a toujours enseigné, dès le collège, à ne faire les applications numériques qu'à la fin.

Mais il est vrai que j'ai été qualifié récemment de très vieux.

maikreeeesse a écrit:

Manu7 a écrit:Oui, c'est intéressant. Nous n'avons pas du tout suivi le même formatage c'est marrant. Moi, mes profs de math refusaient les unités dans les calculs. Et j'ai toujours fait ainsi, et quand on pouvait se passer d'une phrase réponse comme un calcul de volume, on mettait l'unité uniquement au résultat.

Cela dépend peut-être de l'âge, enfin celui de nos professeurs. J'ai sensiblement le même âge que toi et il nous était interdit de mêler les unités dans les calculs tant en terminale C que plus tard en physique et biologie à l'université. L'unité n'apparaissait qu'à la fin, avec l'application numérique. C'est un réflexe qui m'est resté.

Moi aussi. Je trouve très lourde cette pratique qui consiste à mettre les unités dans tous les calculs intermédiaires, que j'ai découverte sur le forum.

Manu7 a écrit:
Certains n'aiment pas la formule de fréquence en % suivante : "eff valeur / eff total * 100", et pourtant elle est très courante dans les livres de maths du collège...

J'utilise cette formule et j'accepte aussi la présentation suivante pour déterminer un pourcentage d'augmentation entre 250 et 261,25 : 11,25*100 / 250 = 4,5%

Deux formules courantes mais fausses, et qui constituent (me semble-t-il) un obstacle à la compréhension de ce qu'est une fréquence dans le premier cas, et de ce qu'est une proportion dans le second cas, et de ce que sont les pourcentages dans les deux cas.

Une longueur n'est pas multipliée par 100 quand on passe son écriture des mètres aux centimètres. Une proportion n'est pas plus multipliée par 100 si on l'écrit en pourcentage.

Si vraiment certains se sentent démuni devant cette idée et veulent absolument voir apparaître une multiplication par 100, ils peuvent multiplier par 100%. Comme 100%, ça fait 1, cela revient à multiplier par 1 et ça ne change pas la valeur elle-même.
11,25/250 * 100% = 4,5%

Mais je conseille d'apprendre plutôt à changer d'unité directement: 0,045 = 4,5%, pas besoin de calcul.

Manu7 a écrit:Oui, c'est intéressant. Nous n'avons pas du tout suivi le même formatage c'est marrant. Moi, mes profs de math refusaient les unités dans les calculs. Et j'ai toujours fait ainsi, et quand on pouvait se passer d'une phrase réponse comme un calcul de volume, on mettait l'unité uniquement au résultat.

Ce n'est pas le formatage que j'avais en tant qu'élève mais le fruit de mes lectures et réflexions postérieures.
Laisser les unités ne pose aucun problème de rigueur mathématique, et cela peut d'ailleurs se formaliser à base d'algèbres tensorielles.

ycombe a écrit:On m'a toujours enseigné, dès le collège, à ne faire les applications numériques qu'à la fin.

C'est l'idéal mais au collège et en 2^nde je préfère ne pas imposer trop directement l'usage du calcul littéral lorsqu'il n'est pas techniquement nécessaire.

Prezbo a écrit:Moi aussi. Je trouve très lourde cette pratique qui consiste à mettre les unités dans tous les calculs intermédiaires, que j'ai découverte sur le forum.

Vide supra. Les élèves qui sont suffisamment à l'aise avec le calcul littéral comprendront vite que faire un calcul littéral + application numérique est la façon la plus simple de respecter le fait que les unités soient toujours précisées.

Personnellement, j'ai changé d'avis sur cette histoire d'unité. Moi aussi j'ai toujours appris à mettre l'unité à la fin.
Mais quand je vois les élèves qui additionnent gaiement des mètres avec des mètres carrés, ou qui multiplient n'importe quoi par n'importe quoi, je trouve que revenir aux unités permet de renforcer le sens. On n'additionne que des unités identiques, un mètre carré, c'est un mètre multiplié par un mètre, un kilomètre par heure c'est un kilomètre divisé par une heure, donc dans le calcul, on doit diviser des kilomètres par des heures, etc... C'est ce qui se faisait en primaire avant les mathématiques modernes apparemment. Et je sais que pour moi-même à partir de la 3ème j'ai toujours vérifié quand j'ai pu mes raisonnements en faisant de l'analyse dimensionnelle à ma sauce. Voire même je m'en servais en première approche pour résoudre les équations du premier degré en physique ou chimie.

Flo44 a écrit:Personnellement, j'ai changé d'avis sur cette histoire d'unité. Moi aussi j'ai toujours appris à mettre l'unité à la fin.
Mais quand je vois les élèves qui additionnent gaiement des mètres avec des mètres carrés, ou qui multiplient n'importe quoi par n'importe quoi, je trouve que revenir aux unités permet de renforcer le sens. On n'additionne que des unités identiques, un mètre carré, c'est un mètre multiplié par un mètre, un kilomètre par heure c'est un kilomètre divisé par une heure, donc dans le calcul, on doit diviser des kilomètres par des heures, etc...

Voilà.

Peut-être aussi qu'en fonction de notre public, l'intérêt qu'on porte à la chose est aussi différent. Ne pas mettre les unités dans les calculs (je fais exception pour le théorème de Pythagore ceci dit) c'est obtenir un résultat dans une unité aléatoire, et je ne vous raconte pas quand il y a une conversion en cours de calcul.

ycombe a écrit:

Mathador a écrit:Si je veux avoir directement le bon résultat, oui, tout comme pour les unités physiques: AB² = AC² + CB² = 16 m² + 9 m² = 25 m² donc AB = 5 m par exemple.
L'alternative est de tout faire en littéral avant l'application numérique, comme on me l'a enseigné en physique en prépa.

On m'a toujours enseigné, dès le collège, à ne faire les applications numériques qu'à la fin.

Mais il est vrai que j'ai été qualifié récemment de très vieux.

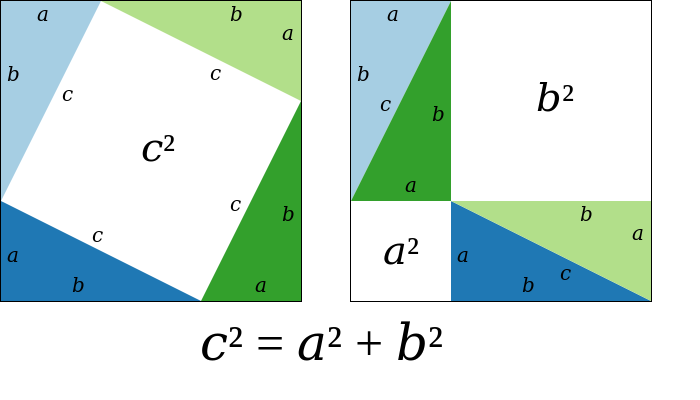
Fenrir a écrit:Ne pas mettre les unités dans les calculs (je fais exception pour le théorème de Pythagore ceci dit) c'est obtenir un résultat dans une unité aléatoire, et je ne vous raconte pas quand il y a une conversion en cours de calcul.

Je ne suis pas certain que je ferais cette exception: les intermédiaires de ces calculs ont un sens géométrique. Surtout si l'on en évoque la preuve suivante:

Effectivement, ma "conversion" aux unités dans les calculs est assez récente (3 ans je crois). Avant je demandais que les unités n'apparaissent que dans les phrases-réponses.
Mais comme @Flo44 j'en ai eu assez de voir additionner des mètres et des kilogrammes et maintenant, j'essaie de formater les élèves dès la 6e. D'après les collègues qui les ont ensuite, ça marche "pas mal" et c'est toujours ça de pris...

A ce propos, j'avais lu attentivement le document suivant issu d'un bulletin de l'APMEP.

Bonjour et merci pour ce thème !

J'ai une question. Pour cet exercice là, donnée en 5e, quelle réponse est attendue par le professeur à votre avis ?

Ecris les fractions suivantes sous forme d’une somme d’un entier et de fractions de même dénominateur, donne ensuite une écriture décimale et une écriture en fraction décimale.
(a) 9/4= ...... + _____
(b) Huit tiers = .......... + ________

2 + 1/4 ; 2,25 et 225/100

Ok, c'est plutôt évident. Mais pour 8/3 ?

8/3 = 2 + 2/3. Ce n'est pas un nombre décimal. (j'accepterais également 2,6, avec la barre en haut du 6, comme écriture décimale, mais l'écriture comme fraction décimale est impossible)
Cependant, je crois surtout que c'est un exercice que je ne donnerais pas tel quel aux élèves. Je rajouterais au moins « le cas échéant » avant de demander l'écriture décimale.

Désolé j'avais pas lu le b, pareil que Mathador.

La dernière fois que j'ai écrit « le cas échéant » dans un énoncé, j'ai eu droit à quelques PLS, une chiée de questions et des cas qui échoyaient même quand ils ne seyaient pas.
Plus jamais ça.

Merci beaucoup pour les réponses.

@VinZT,

Mathador a écrit:

Fenrir a écrit:Ne pas mettre les unités dans les calculs (je fais exception pour le théorème de Pythagore ceci dit) c'est obtenir un résultat dans une unité aléatoire, et je ne vous raconte pas quand il y a une conversion en cours de calcul.

Je ne suis pas certain que je ferais cette exception: les intermédiaires de ces calculs ont un sens géométrique. Surtout si l'on en évoque la preuve suivante:

Oh, mais je suis d'accord, cependant je connais mon public et je sais quand je me tire une balle dans le pied. Voire quand je vide un chargeur.

Pour ma part, l'égalité de Pythagore est une équation, donc je préfère éviter les unités qui risquent d'allourdir la résolution.

Pour revenir sur les pourcentages, quand on fait un tableau de proportionnalité pour trouver les fréquences en %, est-il faux d'écrire le coefficient en bout de tableau ? J'ai déjà eu une discussion avec un puriste sur ce point et sa conclusion était qu'il ne fallait pas faire des tableaux avec des fréquences en %, j'ai trouvé que c'était assez radical comme position surtout qu'au collège c'est très courant comme tableau même si on ne fait plus vraiment les effectifs cumulés, on fait encore un peu des tableaux de fréquences en %. Je sais aussi que l'expression "fréquences en %" peut déranger...

Pourquoi "fréquence en %" dérangerait-elle ?

Et sinon, moi aussi j'ai été formatée à ne pas écrire d'unités dans les calculs... et j'ai commencé à enseigner comme ça, jusqu'à une discussion instructive avec une collègue plus âgée, ayant eu la chance de faire un primaire "à l'ancienne", qui m'a convaincue du contraire. Donc, tant que c'est du calcul pur, oui, je conseille les unités (mais ne les impose pas), par contre dès qu'on passe à des expressions littérales ou à des équations, c'est niet.... et là, les élèves ne comprennent pas la contradiction avec le collègue de l'année précédente.  Bref, y'a un moment où il faut pouvoir se passer des unités et ne les utiliser mentalement que pour des analyses dimensionnelles. Et le tournant c'est à peu près en 4ème il me semble.

Cela dit, % n'est pas une unité mais une façon de dire "centième".

La disparition des unités avec le calcul littéral n'est effective que si l'on dit « Soit x la grandeur bidule en unité truc ». Elle ne s'applique pas en SPC, où les valeurs des variables littérales ont encore une unité.
Pour ce qui est du %, je considère que l'on peut traiter cela comme une unité sans dimension, ce qui permet la conversion en nombre sans unité.

Bonsoir

Dites voir, les collègues en collège, quelles définitions de "chiffres" et "nombres" donnez-vous aux élèves, s'il vous plaît ?
Je suis assez dubitative devant celles dans le cahier du mini-troll en 6ème là (surtout celle pour "chiffre" à vrai dire).

J'avoue ne pas donner de "vraie" définition.
J'explique oralement la différence en faisant le rapprochement avec lettres et mots comme la plupart des profs et j'écris ensuite une phrase du type "0 ; 1 ; 2 ; 3 ; 4 ; 5 ; 6 ; 7 ; 8 et 9 sont les dix chiffres qui servent à écrire les nombres".
Je fais suivre de deux ou trois exemples dont l'un est "4 est un nombre qui s'écrit avec un seul chiffre".
Ma phrase est assez floue car cela ne suffit pas pour l'ensemble des nombres (par exemple les complexes ou les irrationnels nécessitent des symboles supplémentaires) mais c'est suffisant pour les nombres de 6e (sauf pi !) et l'objectif est surtout qu'ils fassent la différence entre chiffres et nombres.

Merci
Je pense que la définition donnée par l'enseignant de mon fils peut justement facilement induire des confusions entre chiffre et nombre à 1 seul chiffre.
"le chiffre est une quantité unitaire, qui est classée dans l'ordre croissant : 0,1,2,3,4,5,6,7,8,9"
Le grand Robert parle simplement des caractères qui servent à écrire les nombres.

Mrs Hobie a écrit:Merci
Je pense que la définition donnée par l'enseignant de mon fils peut justement facilement induire des confusions entre chiffre et nombre à 1 seul chiffre.
"le chiffre est une quantité unitaire, qui est classée dans l'ordre croissant : 0,1,2,3,4,5,6,7,8,9"
Le grand Robert parle simplement des caractères qui servent à écrire les nombres.

D'une part comme tu le fais remarquer un chiffre n'est pas une quantité mais un symbole utilisé pour représenter une quantité, d'autre part je trouve remarquablement confus de méler dans une même phrase une définition (fausse) du chiffre et la liste des chiffres classés par ordre croissant.

Qui est censé comprendre cette phrase ?