Page 1 sur 4 • 1, 2, 3, 4 

 ycombeMonarque
ycombeMonarque

Cette progression charge en 5e/4e, pour respecter les programmes par cycle et permettre aux élèves en difficulté d'avoir plus de temps pour apprendre ce qui est au programme. Pendant ce temps les autres auront de quoi s'occuper avec ce qui est en italique.
J'attends vos avis et suggestions.
_________________
Assurbanipal: "Passant, mange, bois, divertis-toi ; tout le reste n’est rien".
Franck Ramus : "Les sciences de l'éducation à la française se font fort de produire un discours savant sur l'éducation, mais ce serait visiblement trop leur demander que de mettre leur discours à l'épreuve des faits".
 ben2510Expert spécialisé
ben2510Expert spécialisé
Globalement, ça me plaît bien (mais ça fait 9 ans que j'ai quitté le collège).
Arithmétique en cinquième : très bien, mais peut-être peut-on se limiter pour les puissances aux carrés et aux cubes, l'essentiel (à mon sens) étant de traiter les puissances dans le chapitre sur les priorités des opérations.
Peut-être peut-on travailler l'inverse d'une fraction en cinquième, dans la continuité de "prendre une fraction d'un nombre vu en sixième".
Algèbre : prévoir une progression spécifique me semble trèèèèès utile, sans doute faut-il être plus explicite sur les transformations envisagées.
Pour les pourcentages en cinquième, inclus-tu les coefficients multiplicateurs associés à des évolutions relatives ?
Sur les cas d'égalité de triangle, s'agit-il de les énoncer, seulement ? Avec quel statut, d'axiome ou de théorème ?
Tu parles de perpendiculaires en cinquième ; ce n'est plus au programme de sixième ?
En fait, toute la partie géométrie de cinquième ressemble bigrement à l'ancien programme de sixième, non ?
Pour l'algo, j'échangerais tes propositions cinquième et quatrième.
La géométrie de quatrième me semble un peu chargée, essentiellement parce qu'on y retrouve beaucoup de l'ancien programme de cinquième ; pour la géo ana, pourquoi milieu et pas distance ? A cause des r.o.n qui n'arrivent qu'en troisième ? Mais les équations de droites c'est du Thalès, pas du Pythagore.
Gauss, c'est du 2x2 ou bien tu pousses jusqu'à 3x3 ou plus ? Si on reste sur du 2x2 (ce qui est préférable pour l'interprétation graphique), on peut simplement dire "par combinaisons linéaires". Peut-être est-il utile de traiter les cas où les droites sont parallèles, voire confondues, et pas seulement le cas où le point d'intersection est unique ?
Pour le mutex, ils l'auront fait au cycle 2, inutile d'y revenir en troisième :lol:
Bon, je vais me coucher mais je reviens sur ce topic fort intéressant demain :-)
Arithmétique en cinquième : très bien, mais peut-être peut-on se limiter pour les puissances aux carrés et aux cubes, l'essentiel (à mon sens) étant de traiter les puissances dans le chapitre sur les priorités des opérations.
Peut-être peut-on travailler l'inverse d'une fraction en cinquième, dans la continuité de "prendre une fraction d'un nombre vu en sixième".
Algèbre : prévoir une progression spécifique me semble trèèèèès utile, sans doute faut-il être plus explicite sur les transformations envisagées.
Pour les pourcentages en cinquième, inclus-tu les coefficients multiplicateurs associés à des évolutions relatives ?
Sur les cas d'égalité de triangle, s'agit-il de les énoncer, seulement ? Avec quel statut, d'axiome ou de théorème ?
Tu parles de perpendiculaires en cinquième ; ce n'est plus au programme de sixième ?
En fait, toute la partie géométrie de cinquième ressemble bigrement à l'ancien programme de sixième, non ?
Pour l'algo, j'échangerais tes propositions cinquième et quatrième.
La géométrie de quatrième me semble un peu chargée, essentiellement parce qu'on y retrouve beaucoup de l'ancien programme de cinquième ; pour la géo ana, pourquoi milieu et pas distance ? A cause des r.o.n qui n'arrivent qu'en troisième ? Mais les équations de droites c'est du Thalès, pas du Pythagore.
Gauss, c'est du 2x2 ou bien tu pousses jusqu'à 3x3 ou plus ? Si on reste sur du 2x2 (ce qui est préférable pour l'interprétation graphique), on peut simplement dire "par combinaisons linéaires". Peut-être est-il utile de traiter les cas où les droites sont parallèles, voire confondues, et pas seulement le cas où le point d'intersection est unique ?
Pour le mutex, ils l'auront fait au cycle 2, inutile d'y revenir en troisième :lol:
Bon, je vais me coucher mais je reviens sur ce topic fort intéressant demain :-)
- typos:
- identité
es remarquables, homothéties (sans vecteurs ?)
_________________
On fait la science avec des faits, comme on fait une maison avec des pierres : mais une accumulation de faits n'est pas plus une science qu'un tas de pierres n'est une maison. Henri Poincaré La notion d'équation différentielle est le pivot de la conception scientifique du monde. Vladimir Arnold
 ben2510Expert spécialisé
ben2510Expert spécialisé
Je crois que tu as oublié les suites arithmétiques et géométriques en quatrième, et les logarithmes en troisième 

_________________
On fait la science avec des faits, comme on fait une maison avec des pierres : mais une accumulation de faits n'est pas plus une science qu'un tas de pierres n'est une maison. Henri Poincaré La notion d'équation différentielle est le pivot de la conception scientifique du monde. Vladimir Arnold
 verdurinHabitué du forum
verdurinHabitué du forum
ben2510 a écrit:Je crois que tu as oublié les suites arithmétiques et géométriques en quatrième, et les logarithmes en troisième


_________________
Contre la bêtise, les dieux eux mêmes luttent en vain.
Ni centidieux, ni centimètres.
 ycombeMonarque
ycombeMonarque
J'ai pensé que les puissances étaient assez simple pour la cinquième. On pourrait laisser la définition en 5e et les formules de calcul en 4e, avec l'écriture scientifique.ben2510 a écrit:Globalement, ça me plaît bien (mais ça fait 9 ans que j'ai quitté le collège).
Arithmétique en cinquième : très bien, mais peut-être peut-on se limiter pour les puissances aux carrés et aux cubes, l'essentiel (à mon sens) étant de traiter les puissances dans le chapitre sur les priorités des opérations.
Au départ, j'avais mis les 4 opérations sur les fractions en cinquième. Ce n'est pas si mal de tout faire en même temps.
Peut-être peut-on travailler l'inverse d'une fraction en cinquième, dans la continuité de "prendre une fraction d'un nombre vu en sixième".
Ça manquait de place. C'est réduction/factorisation/développement, bien sûr.
Algèbre : prévoir une progression spécifique me semble trèèèèès utile, sans doute faut-il être plus explicite sur les transformations envisagées.
Ah zut, j'ai oublié ça. On va le mettre en quatrième. Ça fera une piqûre de rappel pour les pourcentages.
Pour les pourcentages en cinquième, inclus-tu les coefficients multiplicateurs associés à des évolutions relatives ?
Non théorème.
Sur les cas d'égalité de triangle, s'agit-il de les énoncer, seulement ? Avec quel statut, d'axiome ou de théorème ?
En sixième, c'est juste la notion. Là, il s'agit d'avoir une construction géométrique cohérente, avec les théorèmes. Pour la géométrie j'ai suivi la progression des Lebossé-Hemery 5e/4e (édition de 1958 je pense, peut être plus tôt pour le 5e).
Tu parles de perpendiculaires en cinquième ; ce n'est plus au programme de sixième ? En fait, toute la partie géométrie de cinquième ressemble bigrement à l'ancien programme de sixième, non ?
J'y ai réfléchi. Le ludique, c'est gentil 5 min, je me suis dit qu'il valait mieux commencer par du python en ligne de commande pour voir les bases sur des algorithmes arithmétiques sérieux. Je n'ai mis la partie 4e que parce qu'elle est au programme, mais je la conchie.
Pour l'algo, j'échangerais tes propositions cinquième et quatrième.
Parce que je n'y ai pas pensé. Je vais corriger ça. Distance entre points et équations de cercle en 3e, ça me plait bien.
La géométrie de quatrième me semble un peu chargée, essentiellement parce qu'on y retrouve beaucoup de l'ancien programme de cinquième ; pour la géo ana, pourquoi milieu et pas distance ? A cause des r.o.n qui n'arrivent qu'en troisième ? Mais les équations de droites c'est du Thalès, pas du Pythagore.
2x2 avec le vocabulaire et une méthode utilisable en 3x3 me semble pas mal. Autant aller directement à l'efficace.
Gauss, c'est du 2x2 ou bien tu pousses jusqu'à 3x3 ou plus ? Si on reste sur du 2x2 (ce qui est préférable pour l'interprétation graphique), on peut simplement dire "par combinaisons linéaires". Peut-être est-il utile de traiter les cas où les droites sont parallèles, voire confondues, et pas seulement le cas où le point d'intersection est unique ?
Merci pour ton retour.
Pour le mutex, ils l'auront fait au cycle 2, inutile d'y revenir en troisième :lol:
Bon, je vais me coucher mais je reviens sur ce topic fort intéressant demain :-)
- typos:
es remarquables, homothéties (sans vecteurs ?)
_________________
Assurbanipal: "Passant, mange, bois, divertis-toi ; tout le reste n’est rien".
Franck Ramus : "Les sciences de l'éducation à la française se font fort de produire un discours savant sur l'éducation, mais ce serait visiblement trop leur demander que de mettre leur discours à l'épreuve des faits".
 ycombeMonarque
ycombeMonarque
Oui, tout le début est en commun avec la classe de cinquième. C'est le schéma des anciens programmes, il y avait des parties en commun entre deux niveaux, en révision/approfondissement. Du coup ça peut aller assez vite en quatrième cette partie là.ben2510 a écrit:
La géométrie de quatrième me semble un peu chargée, essentiellement parce qu'on y retrouve beaucoup de l'ancien programme de cinquième
_________________
Assurbanipal: "Passant, mange, bois, divertis-toi ; tout le reste n’est rien".
Franck Ramus : "Les sciences de l'éducation à la française se font fort de produire un discours savant sur l'éducation, mais ce serait visiblement trop leur demander que de mettre leur discours à l'épreuve des faits".
 ycombeMonarque
ycombeMonarque
Seconde tentative:
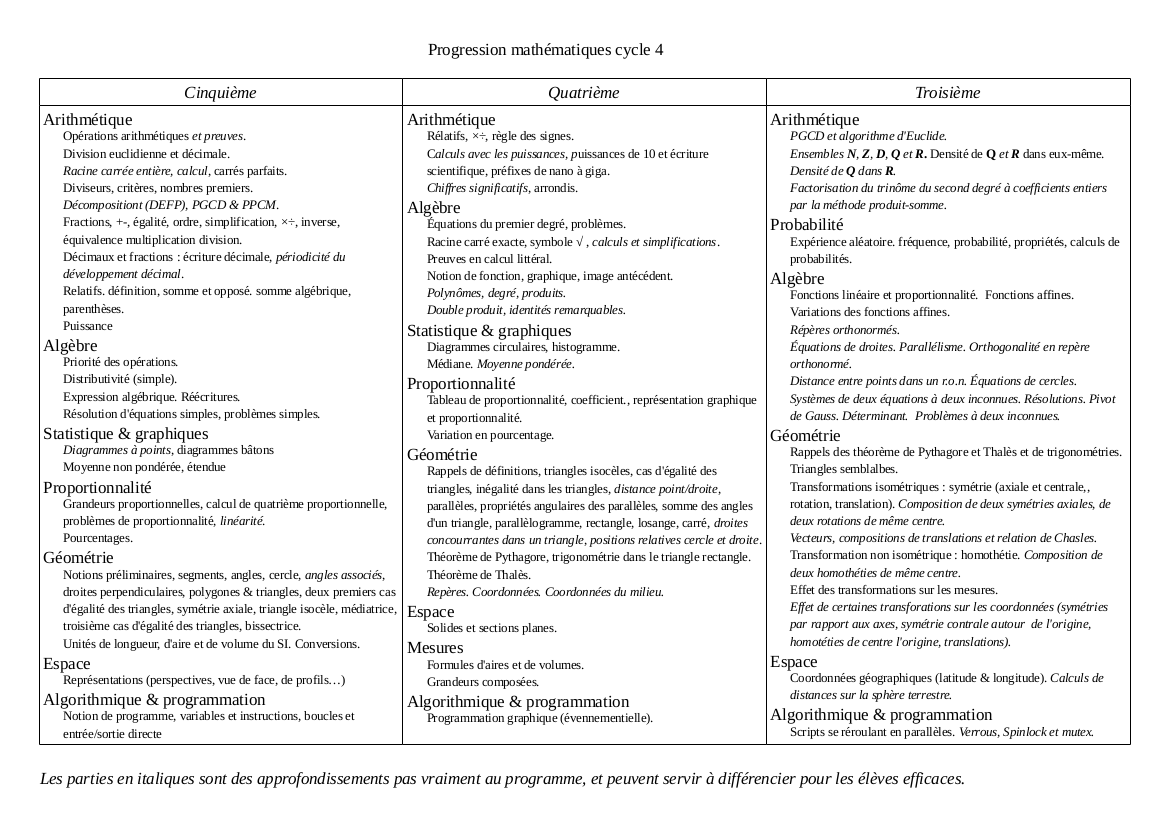
Je viens de voir une autre erreur: homothétie était indiqué hors programme. C'est bien au programme. Je les ai glissées après les vecteurs pour pouvoir les définir vectoriellement pour les élèves qui auront fait les vecteurs.

Je viens de voir une autre erreur: homothétie était indiqué hors programme. C'est bien au programme. Je les ai glissées après les vecteurs pour pouvoir les définir vectoriellement pour les élèves qui auront fait les vecteurs.
_________________
Assurbanipal: "Passant, mange, bois, divertis-toi ; tout le reste n’est rien".
Franck Ramus : "Les sciences de l'éducation à la française se font fort de produire un discours savant sur l'éducation, mais ce serait visiblement trop leur demander que de mettre leur discours à l'épreuve des faits".
 ben2510Expert spécialisé
ben2510Expert spécialisé
Merci pour le boulot !
Quelques remarques encore :
* le fait de travailler sur le "cycle 4" au lieu des quatre niveaux du collège est un piège redoutable, me semble-t-il, car tu fais figurer dans ce programme pas mal de choses qui appartiennent à mon sens aux années précédentes ; p.ex pour le développement périodique d'un rationnel, pour moi ce devrait être vu en sixième (y compris du décimal à développement périodique vers la fraction) ; de même la linéarité en cinquième est déjà vue en CM2, non ? (Sous la forme on peut ajouter des colonnes, des lignes, des combinaisons linéaires d'icelles).
En fait, mais ce n'est aucunement une critique contre toi puisque tu essaies de rester dans le cadre du nouveau programme, j'ai bien l'impression qu'on perd une année de collège.
*Pour le coup, ramener en troisième des choses qui sont passées en seconde il y a quelques années (ou qui ont purement disparu), comme la géo ana et les transformations du plan, signifie qu'on ramène des morceaux de lycée tout en faisant ce qui n'a pas été fait en troisième, ça risque d'être un peu chargé.
*Bien sûr, une quantité importante d'élèves est capable d'aller au bout, voire plus loin (les logarithmes en troisième, ce n'est pas une blague). D'où tes propositions d'approfondissement, qui me semblent bien choisies. Mais pour le coup nous entérinons l'inégalité programmée entre établissements ; les collègues sérieux essaieront d'amener les élèves demandeurs à un bon niveau pour aborder le lycée, tout en s'assurant que tous aient des bases solides (bon c'est notre boulot, hein) tandis qu'une certaine quantité de bras cassés IPR-compatibles brasseront du vent. Tout ça n'est guère satisfaisant.
*Sur les équations de cercle, et les systèmes : en seconde je fais les équations de cercle, et c'est le moment idéal pour attaquer les systèmes non linéaires, pour déterminer les intersections droites/cercles (ou droite conique de manière générale) analytiquement. Si les élèves maitrisent la factorisation avec id rmq, ça roule. Et il y a potentiellement plusieurs solutions, ce qui varie les plaisirs (mais les cas de tangences sont bien aussi). Le cas d'une racine évidente est particulièrement utile.
*Encore un truc : les vecteurs, je suis en train de les reprendre en TS ; le lien avec la Physique est fondamental : préciser qu'en Physique un vecteur a un point d'application ; faire le lien entre produit scalaire et travail d'une force ; l'écriture vectorielle du PFD (deuxième loi de Newton). Sans doute faut-il, dans la mesure du possible voir quels points peuvent être
traités conjointement avec la Phy et la Bio (en TS je m'entends bien avec les collègues de Phy et Bio/Geol du coup on fait beaucoup de ping-pong sur les notions communes : décroissance radioactive, exp, ln, loi binomiale, equas diffs, intégration,complexes (ah non tiens un crétin a supprimé l'électricité), géo dans l'espace ; et vraiment ça plaît bien aux élèves (espérons qu'en plus ce soit efficace)).
* Sur l'algèbre, réécritures avec dev/facto/réd c'est bien, mais je pensais aussi à des choses comme v=d/t <=> d=vt <=> t=d/v (juste la définition d'une fraction), ou bien 68234*756889=51645564026 <=> 51645564026/68234=756889, sans parler de h=1/2 gt² <=> gt²=2h <=> t=racine(2h/g), car vraiment ce genre de manipulations algébriques, qui nécessite de savoir distinguer somme de produit, est le problème numéro 1 en maths au lycée et après (bon, on a la même chose en troisième : résoudre (2x-5)(x+3)=0, puis résoudre (2x-5)+(x+3)=0 et tu plantes 50% des élèves (en seconde on arrive à 75% ), en en TS avec E=hn donc n=h/E
), en en TS avec E=hn donc n=h/E  ).
).
*Dernière chose, pour l'instant : ta logique, qui est excellente, est de faire une lecture exigeante du programme, pour sauver les meubles. Mes remarques viennent de quelqu'un qui ne lit les programmes que très rarement, et seulement pour vérifier que ces programmes sont un sous-ensemble strict de ce qui est fait en cours, donc il faut prendre mes remarques avec des pincettes
Quelques remarques encore :
* le fait de travailler sur le "cycle 4" au lieu des quatre niveaux du collège est un piège redoutable, me semble-t-il, car tu fais figurer dans ce programme pas mal de choses qui appartiennent à mon sens aux années précédentes ; p.ex pour le développement périodique d'un rationnel, pour moi ce devrait être vu en sixième (y compris du décimal à développement périodique vers la fraction) ; de même la linéarité en cinquième est déjà vue en CM2, non ? (Sous la forme on peut ajouter des colonnes, des lignes, des combinaisons linéaires d'icelles).
En fait, mais ce n'est aucunement une critique contre toi puisque tu essaies de rester dans le cadre du nouveau programme, j'ai bien l'impression qu'on perd une année de collège.
*Pour le coup, ramener en troisième des choses qui sont passées en seconde il y a quelques années (ou qui ont purement disparu), comme la géo ana et les transformations du plan, signifie qu'on ramène des morceaux de lycée tout en faisant ce qui n'a pas été fait en troisième, ça risque d'être un peu chargé.
*Bien sûr, une quantité importante d'élèves est capable d'aller au bout, voire plus loin (les logarithmes en troisième, ce n'est pas une blague). D'où tes propositions d'approfondissement, qui me semblent bien choisies. Mais pour le coup nous entérinons l'inégalité programmée entre établissements ; les collègues sérieux essaieront d'amener les élèves demandeurs à un bon niveau pour aborder le lycée, tout en s'assurant que tous aient des bases solides (bon c'est notre boulot, hein) tandis qu'une certaine quantité de bras cassés IPR-compatibles brasseront du vent. Tout ça n'est guère satisfaisant.
*Sur les équations de cercle, et les systèmes : en seconde je fais les équations de cercle, et c'est le moment idéal pour attaquer les systèmes non linéaires, pour déterminer les intersections droites/cercles (ou droite conique de manière générale) analytiquement. Si les élèves maitrisent la factorisation avec id rmq, ça roule. Et il y a potentiellement plusieurs solutions, ce qui varie les plaisirs (mais les cas de tangences sont bien aussi). Le cas d'une racine évidente est particulièrement utile.
*Encore un truc : les vecteurs, je suis en train de les reprendre en TS ; le lien avec la Physique est fondamental : préciser qu'en Physique un vecteur a un point d'application ; faire le lien entre produit scalaire et travail d'une force ; l'écriture vectorielle du PFD (deuxième loi de Newton). Sans doute faut-il, dans la mesure du possible voir quels points peuvent être
traités conjointement avec la Phy et la Bio (en TS je m'entends bien avec les collègues de Phy et Bio/Geol du coup on fait beaucoup de ping-pong sur les notions communes : décroissance radioactive, exp, ln, loi binomiale, equas diffs, intégration,
* Sur l'algèbre, réécritures avec dev/facto/réd c'est bien, mais je pensais aussi à des choses comme v=d/t <=> d=vt <=> t=d/v (juste la définition d'une fraction), ou bien 68234*756889=51645564026 <=> 51645564026/68234=756889, sans parler de h=1/2 gt² <=> gt²=2h <=> t=racine(2h/g), car vraiment ce genre de manipulations algébriques, qui nécessite de savoir distinguer somme de produit, est le problème numéro 1 en maths au lycée et après (bon, on a la même chose en troisième : résoudre (2x-5)(x+3)=0, puis résoudre (2x-5)+(x+3)=0 et tu plantes 50% des élèves (en seconde on arrive à 75%
 ), en en TS avec E=hn donc n=h/E
), en en TS avec E=hn donc n=h/E *Dernière chose, pour l'instant : ta logique, qui est excellente, est de faire une lecture exigeante du programme, pour sauver les meubles. Mes remarques viennent de quelqu'un qui ne lit les programmes que très rarement, et seulement pour vérifier que ces programmes sont un sous-ensemble strict de ce qui est fait en cours, donc il faut prendre mes remarques avec des pincettes
_________________
On fait la science avec des faits, comme on fait une maison avec des pierres : mais une accumulation de faits n'est pas plus une science qu'un tas de pierres n'est une maison. Henri Poincaré La notion d'équation différentielle est le pivot de la conception scientifique du monde. Vladimir Arnold
 Pat BÉrudit
Pat BÉrudit
Je n'ai pas tout regardé en détail. Juste deux-trois points (ce n'est qu'un avis !) :
- tableau de proportionnalité et coefficient : je verrais ça dès la 5ème (à ce propos, en 5ème, quand tu parles du calcul d'une quatrième proportionnelle tu ne penses pas "produit en croix", j'imagine, juste l'ancienne "règle de trois" ? Parce que le produit en croix, via des égalités de fractions, ça passe assez bien par la notion de coef et de le tableau)
- j'aurais commencé l'algorithmique en 4ème seulement, pour voir la notion de variable informatique une fois que celle d'expression littérale est bien stabilisée (même si effectivement ça peut apporter un autre sens, une motivation, à l'utilisation d'une lettre; ça se discute). Et les boucles, ça me semble chaud en 5ème... j'en connais qui ont du mal au lycée !
- détail, en stat : pour moi, l'étendue, ça colle bien avec la médiane aussi, et voir étendue /médiane / moyenne simple ensemble, en "tensions", pourrait être efficace, que ce soit en 5ème ou en 4ème...
- travailler sur les unités de volumes se fait au moment où on calcule des volumes... je ferais donc des calculs de volumes (avec utilisation de formules, donc des expressions littérales) en 5ème ; on peut y ajouter un travail sur d'autres types d'unités (en prévision des grandeurs-composées en 4ème)
- en géométrie, je chargerais davantage la 5ème (par ex en y mettant tout ce qui concerne les triangles), ça me semble trop chargé en 4ème
- La trigo, c'est abstrait, ça me semble un peu tôt en 4ème, je passerais en 3ème (en tout cas, quand j'étais élève, j'avais eu beaucoup de mal à la comprendre, en 3ème)
- le PGCD (simple approfondissement) se ferait très bien en 4ème, avec réactivation des décomposition en facteur premier (avant de passer à l'algo d'euclide)
Après, ce que je dis charge trop la 5ème... passer quoi en 4ème ? Division de fractions (pour tout réactiver) ou puissances peut-être ?
Bon, sinon, je déteste ce programme... mais je ne suis pas la seule!
Je me dis que les programmes actuels ayant été mûrement réfléchi en haut lieu (en tout cas plus que les futurs programmes), il faut peut-être essayer de ne pas trop s'écarter de leur logique ?
A mon avis, il ne faut pas trop forcer sur l'algorithmique mais vraiment assurer les bases nécessaires pour la suite des études, notamment scientifique....
Et c'est rudement exigeant quand on prend ce qui est italique, j'ai les 3/4 de mes élèves qui n'en seront pas capables (pas avec 3h30 par semaine en tout cas)... Et pourtant ça serait bien qu'ils fassent tous une partie de ce qui est en italique (systèmes, identités remarquables et équations produit c'est rudement important)...
Et j'avais pas réalisé qu'ils avaient autant décalé la géométrie... qu'ils en faisaient si peu en cycle 3... Tu es sûr qu'ils ne maitrisent pas déjà les perpendiculaires ou un peu les angles en arrivant en 5ème ?
- tableau de proportionnalité et coefficient : je verrais ça dès la 5ème (à ce propos, en 5ème, quand tu parles du calcul d'une quatrième proportionnelle tu ne penses pas "produit en croix", j'imagine, juste l'ancienne "règle de trois" ? Parce que le produit en croix, via des égalités de fractions, ça passe assez bien par la notion de coef et de le tableau)
- j'aurais commencé l'algorithmique en 4ème seulement, pour voir la notion de variable informatique une fois que celle d'expression littérale est bien stabilisée (même si effectivement ça peut apporter un autre sens, une motivation, à l'utilisation d'une lettre; ça se discute). Et les boucles, ça me semble chaud en 5ème... j'en connais qui ont du mal au lycée !
- détail, en stat : pour moi, l'étendue, ça colle bien avec la médiane aussi, et voir étendue /médiane / moyenne simple ensemble, en "tensions", pourrait être efficace, que ce soit en 5ème ou en 4ème...
- travailler sur les unités de volumes se fait au moment où on calcule des volumes... je ferais donc des calculs de volumes (avec utilisation de formules, donc des expressions littérales) en 5ème ; on peut y ajouter un travail sur d'autres types d'unités (en prévision des grandeurs-composées en 4ème)
- en géométrie, je chargerais davantage la 5ème (par ex en y mettant tout ce qui concerne les triangles), ça me semble trop chargé en 4ème
- La trigo, c'est abstrait, ça me semble un peu tôt en 4ème, je passerais en 3ème (en tout cas, quand j'étais élève, j'avais eu beaucoup de mal à la comprendre, en 3ème)
- le PGCD (simple approfondissement) se ferait très bien en 4ème, avec réactivation des décomposition en facteur premier (avant de passer à l'algo d'euclide)
Après, ce que je dis charge trop la 5ème... passer quoi en 4ème ? Division de fractions (pour tout réactiver) ou puissances peut-être ?
Bon, sinon, je déteste ce programme... mais je ne suis pas la seule!
Je me dis que les programmes actuels ayant été mûrement réfléchi en haut lieu (en tout cas plus que les futurs programmes), il faut peut-être essayer de ne pas trop s'écarter de leur logique ?
A mon avis, il ne faut pas trop forcer sur l'algorithmique mais vraiment assurer les bases nécessaires pour la suite des études, notamment scientifique....
Et c'est rudement exigeant quand on prend ce qui est italique, j'ai les 3/4 de mes élèves qui n'en seront pas capables (pas avec 3h30 par semaine en tout cas)... Et pourtant ça serait bien qu'ils fassent tous une partie de ce qui est en italique (systèmes, identités remarquables et équations produit c'est rudement important)...
Et j'avais pas réalisé qu'ils avaient autant décalé la géométrie... qu'ils en faisaient si peu en cycle 3... Tu es sûr qu'ils ne maitrisent pas déjà les perpendiculaires ou un peu les angles en arrivant en 5ème ?
 cubeNiveau 8
cubeNiveau 8
Je suppose que c'est un choix délibéré de ne pas suivre les "repères de progressivité" indiqués dans le programme ? Par exemple, "le théorème de Thalès est introduit en 3ème". Non pas que ça me pose un problème de conscience, hein ! 
Il y presque plus de "hors-programme" que de "programme", en fait !! Et, même si ce sont des notions importantes, et qui vont manquer aux élèves au lycée (comme les systèmes d'équation, par exemple), je ne suis pas sûre d'arriver à faire tout cela en trois misérables heures et demi par semaine... (surtout si un EPI vient bouffer du temps)
Bref, l'EN aurait mieux fait de laisser ycombe nous concocter les programmes de collège, au moins il auraient eu du contenu ...

Il y presque plus de "hors-programme" que de "programme", en fait !! Et, même si ce sont des notions importantes, et qui vont manquer aux élèves au lycée (comme les systèmes d'équation, par exemple), je ne suis pas sûre d'arriver à faire tout cela en trois misérables heures et demi par semaine... (surtout si un EPI vient bouffer du temps)
Bref, l'EN aurait mieux fait de laisser ycombe nous concocter les programmes de collège, au moins il auraient eu du contenu ...

 ycombeMonarque
ycombeMonarque
Merci pour vos réactions à tous.
Je vais répondre au reste après, mais pour les repères de progressivités, c'est un choix délibéré de les ignorer. Ils me semblent carrément nuls: charger en troisième alors qu'on est dans une logique de cycle sans redoublement, c'est stupide. Je pense que c'est une meilleure idée d'en faire le plus possible les deux premières années, pour pouvoir différencier la troisième année avec les approfondissements pour ceux qui ont pigé et reprendre l'essentiel pour les autres. D'où l'idée d'inscrire des approfondissements dans la répartition (et de les raccrocher au lycée tant qu'à faire, je n'oublie pas que nous préparons une majorité d'élèves à partir en seconde générale).
Je vais répondre au reste après, mais pour les repères de progressivités, c'est un choix délibéré de les ignorer. Ils me semblent carrément nuls: charger en troisième alors qu'on est dans une logique de cycle sans redoublement, c'est stupide. Je pense que c'est une meilleure idée d'en faire le plus possible les deux premières années, pour pouvoir différencier la troisième année avec les approfondissements pour ceux qui ont pigé et reprendre l'essentiel pour les autres. D'où l'idée d'inscrire des approfondissements dans la répartition (et de les raccrocher au lycée tant qu'à faire, je n'oublie pas que nous préparons une majorité d'élèves à partir en seconde générale).
_________________
Assurbanipal: "Passant, mange, bois, divertis-toi ; tout le reste n’est rien".
Franck Ramus : "Les sciences de l'éducation à la française se font fort de produire un discours savant sur l'éducation, mais ce serait visiblement trop leur demander que de mettre leur discours à l'épreuve des faits".
 ycombeMonarque
ycombeMonarque
Pas de quoi. Merci pour les retours. Dans mon esprit, comme pour l'analyse des programmes, c'est un travail collectif. Je propose une base, imparfaite mais pour lancer une discussion, et je la corrige en suivant vos idées.ben2510 a écrit:Merci pour le boulot !
Sur le fond, tu sais qu'on est d'accord. Je compte m'attaquer aussi au cycle 3 (amis PE, restez à l'écoute) même si je sais bien que j'aurai plus de mal à la faire passer, les IEN ayant de gros moyen de pression sur les PE.
Quelques remarques encore :
* le fait de travailler sur le "cycle 4" au lieu des quatre niveaux du collège est un piège redoutable, me semble-t-il, car tu fais figurer dans ce programme pas mal de choses qui appartiennent à mon sens aux années précédentes ; p.ex pour le développement périodique d'un rationnel, pour moi ce devrait être vu en sixième (y compris du décimal à développement périodique vers la fraction) ; de même la linéarité en cinquième est déjà vue en CM2, non ? (Sous la forme on peut ajouter des colonnes, des lignes, des combinaisons linéaires d'icelles).
Tu as raison mais je vais le lire différemment: la sixième est une année de remise à plat et d'approfondissement de ce qui a été vu au primaire, comme la seconde par rapport au collège. C'est comme ça qu'étais batis les programmes autrefois (le LH de sixième en est une très belle illustration). À la 5e l'entrée dans la géométrie déductive et dans l'algèbre.
En fait, mais ce n'est aucunement une critique contre toi puisque tu essaies de rester dans le cadre du nouveau programme, j'ai bien l'impression qu'on perd une année de collège.
Dans mon esprit les opérations arithmétiques, preuves, opérations sur les fractions, proportionnalité et pourcentages devraient être au cycle 3. Elles sont au cycle 4 je fais avec, je les mettrai en approfondissement pour le cycle 3.
Non, il y a eu pas mal d'allègements. Et plus on en fait, mieux les élèves comprennent. Il ne t'échappera pas que j'ai choisi en approfondissement au maximum ce qui fait lien entre plusieurs chapitre (géo ana et vecteurs notamment).
*Pour le coup, ramener en troisième des choses qui sont passées en seconde il y a quelques années (ou qui ont purement disparu), comme la géo ana et les transformations du plan, signifie qu'on ramène des morceaux de lycée tout en faisant ce qui n'a pas été fait en troisième, ça risque d'être un peu chargé.
C'est le cas depuis longtemps mais à part répéter sans arrêt qu'il faut aller plus loin, je ne vois pas quoi faire d'autre.
*Bien sûr, une quantité importante d'élèves est capable d'aller au bout, voire plus loin (les logarithmes en troisième, ce n'est pas une blague). D'où tes propositions d'approfondissement, qui me semblent bien choisies. Mais pour le coup nous entérinons l'inégalité programmée entre établissements ; les collègues sérieux essaieront d'amener les élèves demandeurs à un bon niveau pour aborder le lycée, tout en s'assurant que tous aient des bases solides (bon c'est notre boulot, hein) tandis qu'une certaine quantité de bras cassés IPR-compatibles brasseront du vent. Tout ça n'est guère satisfaisant.
On peut détailler: Réduction/developper/factoriser/isoler une inconnue.
*Sur les équations de cercle, et les systèmes : en seconde je fais les équations de cercle, et c'est le moment idéal pour attaquer les systèmes non linéaires, pour déterminer les intersections droites/cercles (ou droite conique de manière générale) analytiquement. Si les élèves maitrisent la factorisation avec id rmq, ça roule. Et il y a potentiellement plusieurs solutions, ce qui varie les plaisirs (mais les cas de tangences sont bien aussi). Le cas d'une racine évidente est particulièrement utile.
*Encore un truc : les vecteurs, je suis en train de les reprendre en TS ; le lien avec la Physique est fondamental : préciser qu'en Physique un vecteur a un point d'application ; faire le lien entre produit scalaire et travail d'une force ; l'écriture vectorielle du PFD (deuxième loi de Newton). Sans doute faut-il, dans la mesure du possible voir quels points peuvent être
traités conjointement avec la Phy et la Bio (en TS je m'entends bien avec les collègues de Phy et Bio/Geol du coup on fait beaucoup de ping-pong sur les notions communes : décroissance radioactive, exp, ln, loi binomiale, equas diffs, intégration,complexes(ah non tiens un crétin a supprimé l'électricité), géo dans l'espace ; et vraiment ça plaît bien aux élèves (espérons qu'en plus ce soit efficace)).
* Sur l'algèbre, réécritures avec dev/facto/réd c'est bien, mais je pensais aussi à des choses comme v=d/t <=> d=vt <=> t=d/v (juste la définition d'une fraction), ou bien 68234*756889=51645564026 <=> 51645564026/68234=756889, sans parler de h=1/2 gt² <=> gt²=2h <=> t=racine(2h/g), car vraiment ce genre de manipulations algébriques, qui nécessite de savoir distinguer somme de produit, est le problème numéro 1 en maths au lycée et après (bon, on a la même chose en troisième : résoudre (2x-5)(x+3)=0, puis résoudre (2x-5)+(x+3)=0 et tu plantes 50% des élèves (en seconde on arrive à 75%), en en TS avec E=hn donc n=h/E
).
Les programmes ne sont jamais que des titres de chapitre, Le contenu (comme les liens avec la physique) c'est le boulot de l'enseignant.
*Dernière chose, pour l'instant : ta logique, qui est excellente, est de faire une lecture exigeante du programme, pour sauver les meubles. Mes remarques viennent de quelqu'un qui ne lit les programmes que très rarement, et seulement pour vérifier que ces programmes sont un sous-ensemble strict de ce qui est fait en cours, donc il faut prendre mes remarques avec des pincettes
_________________
Assurbanipal: "Passant, mange, bois, divertis-toi ; tout le reste n’est rien".
Franck Ramus : "Les sciences de l'éducation à la française se font fort de produire un discours savant sur l'éducation, mais ce serait visiblement trop leur demander que de mettre leur discours à l'épreuve des faits".
 ycombeMonarque
ycombeMonarque
Pat B a écrit:Je n'ai pas tout regardé en détail. Juste deux-trois points (ce n'est qu'un avis !) :
- tableau de proportionnalité et coefficient : je verrais ça dès la 5ème (à ce propos, en 5ème, quand tu parles du calcul d'une quatrième proportionnelle tu ne penses pas "produit en croix", j'imagine, juste l'ancienne "règle de trois" ? Parce que le produit en croix, via des égalités de fractions, ça passe assez bien par la notion de coef et de le tableau)
Je suis pour la suppression du tableau de proportionnalité des programmes. C'est une survivance de l'époque des mathématiques modernes qui est plus nuisible qu'autre chose.
Quatrième proportionnelle, c'est produit en croix ou règle de trois, peu importe.
Je pense qu'il faut commencer tôt ou ne pas le faire du tout. On prend le temps de le faire tout au long du cycle 3 ou on le fait en 3h en juin avant le DNB (et il n'en restera rien).
- j'aurais commencé l'algorithmique en 4ème seulement, pour voir la notion de variable informatique une fois que celle d'expression littérale est bien stabilisée (même si effectivement ça peut apporter un autre sens, une motivation, à l'utilisation d'une lettre; ça se discute). Et les boucles, ça me semble chaud en 5ème... j'en connais qui ont du mal au lycée !
On pourrait mettre moyenne, médiane, mode, étendue en cinquième tu penses ? Pourquoi pas.
- détail, en stat : pour moi, l'étendue, ça colle bien avec la médiane aussi, et voir étendue /médiane / moyenne simple ensemble, en "tensions", pourrait être efficace, que ce soit en 5ème ou en 4ème...
Les calculs de volume sont au cycle 3, il me semble. Les conversions ne sont nulle part. On pourra les ajouter aussi en sixième.
- travailler sur les unités de volumes se fait au moment où on calcule des volumes... je ferais donc des calculs de volumes (avec utilisation de formules, donc des expressions littérales) en 5ème ; on peut y ajouter un travail sur d'autres types d'unités (en prévision des grandeurs-composées en 4ème)
Il y a beaucoup de révisions en quatrièmes. De trucs repris de la cinquième. mais d'accord, je vais y réfléchlr.
- en géométrie, je chargerais davantage la 5ème (par ex en y mettant tout ce qui concerne les triangles), ça me semble trop chargé en 4ème
Je pense mieux de la faire tôt pour pouvoir la reprendre en troisième si besoin.
- La trigo, c'est abstrait, ça me semble un peu tôt en 4ème, je passerais en 3ème (en tout cas, quand j'étais élève, j'avais eu beaucoup de mal à la comprendre, en 3ème)
D'ailleurs, et si on ajoutait les projections pour introduire le cosinus comme coefficiert de projection orthogonale ?
PGCD PPCM par la DEFP c'est simple. Et ça sert pour les calculs de fractions. Je le garde en cinnquième, c'est mieux.
- le PGCD (simple approfondissement) se ferait très bien en 4ème, avec réactivation des décomposition en facteur premier (avant de passer à l'algo d'euclide)
Après, ce que je dis charge trop la 5ème... passer quoi en 4ème ? Division de fractions (pour tout réactiver) ou puissances peut-être ?
Bon, sinon, je déteste ce programme... mais je ne suis pas la seule!
Je me dis que les programmes actuels ayant été mûrement réfléchi en haut lieu (en tout cas plus que les futurs programmes), il faut peut-être essayer de ne pas trop s'écarter de leur logique ?


Tu as encore beaucoup d'illusions… Les programmes actuels résultent d'allègements et de petites modifications régulières de ceux de 1985, ceux qui ont mis fin aux maths modernes. Ceux-ci ont été publiés en catastrophe parce qu'un ministre voulait laisser sa marque.
Les derniers programmes conçus globalement et de manière cohérente étaient ceux des maths modernes. Leurs concepteurs avaient juste oublié de se demander de quoi un enfant était capable comme abstraction… Mais au final ils étaient meilleurs et plus exigeants que les actuels.
Il y en a en cycle 3. Là, on reprend avec de jolis théorèmes, pour entrer dans la géométrie déductive.
A mon avis, il ne faut pas trop forcer sur l'algorithmique mais vraiment assurer les bases nécessaires pour la suite des études, notamment scientifique....
Et c'est rudement exigeant quand on prend ce qui est italique, j'ai les 3/4 de mes élèves qui n'en seront pas capables (pas avec 3h30 par semaine en tout cas)... Et pourtant ça serait bien qu'ils fassent tous une partie de ce qui est en italique (systèmes, identités remarquables et équations produit c'est rudement important)...
Et j'avais pas réalisé qu'ils avaient autant décalé la géométrie... qu'ils en faisaient si peu en cycle 3... Tu es sûr qu'ils ne maitrisent pas déjà les perpendiculaires ou un peu les angles en arrivant en 5ème ?
_________________
Assurbanipal: "Passant, mange, bois, divertis-toi ; tout le reste n’est rien".
Franck Ramus : "Les sciences de l'éducation à la française se font fort de produire un discours savant sur l'éducation, mais ce serait visiblement trop leur demander que de mettre leur discours à l'épreuve des faits".
 ben2510Expert spécialisé
ben2510Expert spécialisé
On peut faire de la géométrie déductive en sixième ; plus précisément l'enseignant peut faire de la géométrie déductive en sixième, histoire de débattre un peu et de motiver les résultats du cours, même si il est sans doute tôt pour demander aux élèves de rédiger proprement un raisonnement déductif.
Typiquement, la construction d'une bissectrice avec un compas et un losange, ou bien une parallèle au compas, une perpendiculaire (tout ce qui tourne autour du losange), ou bien la reproduction d'un angle au compas avec un triangle isocèle... ont besoin d'être démontrées aux élèves, ce qui leur donne de bonnes habitudes (bon, à mon avis).
Tiens, cela m'amène à une question (qui sent le Al-Kashi et le développement limité à plein nez) : pour reproduire un angle de sommet O au compas, avec A et B sur les côtés, vaut-il mieux que OAB soit isocèle en O ou en A ? Sans doute faut-il discuter en fonction de la mesure de l'angle ? :gratte:
Typiquement, la construction d'une bissectrice avec un compas et un losange, ou bien une parallèle au compas, une perpendiculaire (tout ce qui tourne autour du losange), ou bien la reproduction d'un angle au compas avec un triangle isocèle... ont besoin d'être démontrées aux élèves, ce qui leur donne de bonnes habitudes (bon, à mon avis).
Tiens, cela m'amène à une question (qui sent le Al-Kashi et le développement limité à plein nez) : pour reproduire un angle de sommet O au compas, avec A et B sur les côtés, vaut-il mieux que OAB soit isocèle en O ou en A ? Sans doute faut-il discuter en fonction de la mesure de l'angle ? :gratte:
_________________
On fait la science avec des faits, comme on fait une maison avec des pierres : mais une accumulation de faits n'est pas plus une science qu'un tas de pierres n'est une maison. Henri Poincaré La notion d'équation différentielle est le pivot de la conception scientifique du monde. Vladimir Arnold
 ycombeMonarque
ycombeMonarque
Troisième version.
Modifications:
− J'ai nettoyé ce qui est en cycle 3.
− J'ai ôté tout ce qui était rappel, en me disant qu'en enseignant savait ce qu'il avait à faire.
− J'ai glissé tout le travail sur les triangles en cinquième, et ajouté le théorème des milieux entre les parallélogrammes et les droites concourantes des triangles.
− J'ai ajouté «isoler une variable dans une expression» en quatrième.
− J'ai créé une section «Géométrie analytique» pour la mettre en évidence.

Modifications:
− J'ai nettoyé ce qui est en cycle 3.
− J'ai ôté tout ce qui était rappel, en me disant qu'en enseignant savait ce qu'il avait à faire.
− J'ai glissé tout le travail sur les triangles en cinquième, et ajouté le théorème des milieux entre les parallélogrammes et les droites concourantes des triangles.
− J'ai ajouté «isoler une variable dans une expression» en quatrième.
− J'ai créé une section «Géométrie analytique» pour la mettre en évidence.

_________________
Assurbanipal: "Passant, mange, bois, divertis-toi ; tout le reste n’est rien".
Franck Ramus : "Les sciences de l'éducation à la française se font fort de produire un discours savant sur l'éducation, mais ce serait visiblement trop leur demander que de mettre leur discours à l'épreuve des faits".
 TFSFidèle du forum
TFSFidèle du forum
Cher Yves,
Ta proposition de répartition est fort belle et très motivante pour nous... et peut-être parviendrons nous à la mettre en place d'ici trois ans... même s'il faudrait avoir une idée des futurs programmes du lycée pour le dire...(développement de la géométrie analytique ou retour des transformations ? approfondissement du calcul algébrique ou compléments de calculs sur les puissances et les radicaux ?)
Il me semble par contre que dans l'immédiat notre problématique n'est pas celle à laquelle tu as répondu...
Je crois qu'il nous faut en effet prévoir une progression de cycle "à l'envers" depuis la 3ème jusqu'à la 5ème (et pourquoi pas la sixième...) et répondre pour chaque niveau à deux questions; qu'est ce qui a été fait avec les anciens programmes les années n-1, n-2... et que reste-t-il à réaliser en année n.
En réfléchissant de cette manière, il y a peu de place à des approfondissement en 3ème puisque Thalès, Trigo, Fonctions, Probas sont bien toujours à faire et qu'il va bien falloir faire toute l'Algo du cycle et les Transformations... tout cela avec au moins 1/2 heure de cours en moins (sur l'année cela fait 1 mois !).
Sur les autres niveaux, c'est un peu moins tendu (mais attention aux EPI et AP chronophages...) et on pourra surement commencer à "étaler" plus harmonieusement les nouveaux et les anciens thèmes un peu à ta façon... mais probablement pas d'un coup d'un seul !
Ta proposition de répartition est fort belle et très motivante pour nous... et peut-être parviendrons nous à la mettre en place d'ici trois ans... même s'il faudrait avoir une idée des futurs programmes du lycée pour le dire...(développement de la géométrie analytique ou retour des transformations ? approfondissement du calcul algébrique ou compléments de calculs sur les puissances et les radicaux ?)
Il me semble par contre que dans l'immédiat notre problématique n'est pas celle à laquelle tu as répondu...
Je crois qu'il nous faut en effet prévoir une progression de cycle "à l'envers" depuis la 3ème jusqu'à la 5ème (et pourquoi pas la sixième...) et répondre pour chaque niveau à deux questions; qu'est ce qui a été fait avec les anciens programmes les années n-1, n-2... et que reste-t-il à réaliser en année n.
En réfléchissant de cette manière, il y a peu de place à des approfondissement en 3ème puisque Thalès, Trigo, Fonctions, Probas sont bien toujours à faire et qu'il va bien falloir faire toute l'Algo du cycle et les Transformations... tout cela avec au moins 1/2 heure de cours en moins (sur l'année cela fait 1 mois !).
Sur les autres niveaux, c'est un peu moins tendu (mais attention aux EPI et AP chronophages...) et on pourra surement commencer à "étaler" plus harmonieusement les nouveaux et les anciens thèmes un peu à ta façon... mais probablement pas d'un coup d'un seul !
 William FosterExpert
William FosterExpert
Bah je dirais que nous avons 3 problèmes à résoudre :
- quel programme pour les élèves qui entrent en 5° en 2016 ?
- quel programme pour les élèves qui entrent en 4° en 2016 ?
- quel programme pour les élèves qui entrent en 3° en 2016 ?
La proposition d'Ycombe permet déjà d'essayer d'en régler un (le premier en l’occurrence). Et rien que pour cet effort, moi je dis bravo et merci
et merci 
Par contre, il reste encore les deux autres soucis à régler ET à adapter le programme de 3° à ce qu'il pourrait y avoir en 2°.
Rajoutons à la tambouille que l'on ne sait pas a priori combien d'heures vont être bouffées par les Enseignements Complémentaires...
Ensuite, saupoudrons un peu d'incertitude pour la flexibilité du nombre d'heures par année (le coup de 4h en 4° et 3h en 3° pour qu'au final ça fasse le bon compte). :gouteur:
Oui, bon, je sais... Faut que j'arrête de râler : c'est pas tout pourri. C'eut pu être pire et qu'on ait aussi à faire tout ce travail pour le cycle 3... :|
- quel programme pour les élèves qui entrent en 5° en 2016 ?
- quel programme pour les élèves qui entrent en 4° en 2016 ?
- quel programme pour les élèves qui entrent en 3° en 2016 ?
La proposition d'Ycombe permet déjà d'essayer d'en régler un (le premier en l’occurrence). Et rien que pour cet effort, moi je dis bravo
 et merci
et merci Par contre, il reste encore les deux autres soucis à régler ET à adapter le programme de 3° à ce qu'il pourrait y avoir en 2°.
Rajoutons à la tambouille que l'on ne sait pas a priori combien d'heures vont être bouffées par les Enseignements Complémentaires...
Ensuite, saupoudrons un peu d'incertitude pour la flexibilité du nombre d'heures par année (le coup de 4h en 4° et 3h en 3° pour qu'au final ça fasse le bon compte). :gouteur:
Oui, bon, je sais... Faut que j'arrête de râler : c'est pas tout pourri. C'eut pu être pire et qu'on ait aussi à faire tout ce travail pour le cycle 3... :|
_________________
Tout le monde me dit que je ne peux pas faire l'unanimité.
"Opinions are like orgasms : mine matters most and I really don't care if you have one." Sylvia Plath
Vérificateur de miroir est un métier que je me verrais bien faire, un jour.
 Samuel DMNiveau 6
Samuel DMNiveau 6
D'après ce qui se dit, le lycée n'aura sûrement pas de changement de programme avant que la prochaine majorité n'arrive au pouvoir.
Merci beaucoup ycombe pour ton travail. Je vais orienter des collègues vers ce fil pour qu'ils constatent que l'on peut détourner le futur programme pour faire de vraies math!
Merci beaucoup ycombe pour ton travail. Je vais orienter des collègues vers ce fil pour qu'ils constatent que l'on peut détourner le futur programme pour faire de vraies math!
 William FosterExpert
William FosterExpert
Samuel DM a écrit:D'après ce qui se dit, le lycée n'aura sûrement pas de changement de programme avant que la prochaine majorité n'arrive au pouvoir.
D'après ce qui se dit où ? Ça me fait penser au sketch de Coluche sur les milieux autorisés à penser :lol:
Si après modification du programme de 3° il n'y a pas modification du programme de 2°, on en déduira que celui de 3° a finalement été adapté à celui de 2°, ce qui voudra dire qu'il était actuellement inadapté. Or, il n'est pas envisageable que nos encadrants se soient à ce point fourvoyés.

Ou alors, cela voudrait dire que finalement, les élèves auront les mêmes connaissances avant et après... Dans ce cas, pourquoi changer les programmes ?

Je ne vois pas comment on peut soutenir que les nouveaux programmes ont été faits du point de vue des élèves ET justifier qu'il n'y ait pas de changement au lycée. Mais bon, ce n'est pas parce que je ne vois pas de solution qu'il n'y en a pas
_________________
Tout le monde me dit que je ne peux pas faire l'unanimité.
"Opinions are like orgasms : mine matters most and I really don't care if you have one." Sylvia Plath
Vérificateur de miroir est un métier que je me verrais bien faire, un jour.
 leskhalNiveau 9
leskhalNiveau 9
Les lycéens qui sortiront du collège2016™ seront encore plus incompétents quel leurs camarades actuels, leur plaquer les mêmes programmes en seconde relève du plantage assuré. Ça désengorgera peut-être les classes de 1S encombrées d'élèves qui n'ont rien à y faire...
_________________
 ycombeMonarque
ycombeMonarque
Bon alors à titre transitoire, pour les élèves qui vont entrer en quatième
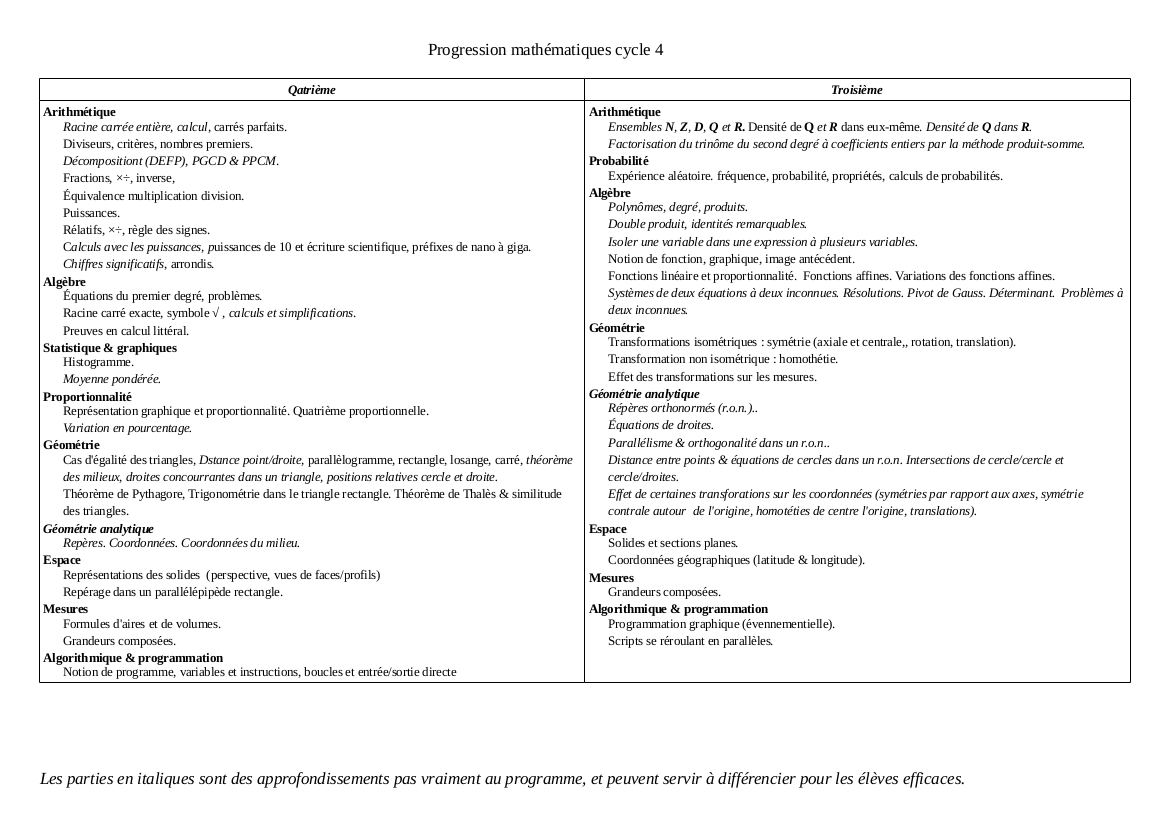
Au fait, ceux qui ont eu des débuts de (mal)formation, est-ce que quelqu'un a posé la question des allègements pour ceux qui entrent en troisième ?

Au fait, ceux qui ont eu des débuts de (mal)formation, est-ce que quelqu'un a posé la question des allègements pour ceux qui entrent en troisième ?
_________________
Assurbanipal: "Passant, mange, bois, divertis-toi ; tout le reste n’est rien".
Franck Ramus : "Les sciences de l'éducation à la française se font fort de produire un discours savant sur l'éducation, mais ce serait visiblement trop leur demander que de mettre leur discours à l'épreuve des faits".
 William FosterExpert
William FosterExpert
Pas personnellement, mais j'ai ouï dire qu'on comptait sur nous pour savoir s'adapter... 

_________________
Tout le monde me dit que je ne peux pas faire l'unanimité.
"Opinions are like orgasms : mine matters most and I really don't care if you have one." Sylvia Plath
Vérificateur de miroir est un métier que je me verrais bien faire, un jour.
 pailleauquebecFidèle du forum
pailleauquebecFidèle du forum
Mon sentiment : (je ne détiens pas la vérité)
Je pense qu'il faut impérativement charger plus le niveau sixième qui aura 4h30 et faire une progression 6 5 4 3. Il faut déplacer des notions de 5e en 6e.
Il faut prévoir pour chaque leçon 2 niveaux : basique et avancé.
En effet il y aura beaucoup d'heures dédoublées à cause de la marge.
Il faut donc faire les même notions à deux niveaux différents d'approfondissement.
Par exemple : avec le groupe des bons en maths tu fais la preuve et avec l'autre groupe seulement l'entraînement basique.
On peut ainsi voir certaines techniques avancées avec un groupe et pas l'autre.
Je n'ai pas le temps là, mais je vais te donner ma propre idée de progression.
Il faut encore que je compile mes sources, tout n'est pas prêt.
Peux-tu mettre ta progression en texte pour qu'on puisse commenter simplement (l'image c'est pas pratique) ?
Je pense qu'il faut impérativement charger plus le niveau sixième qui aura 4h30 et faire une progression 6 5 4 3. Il faut déplacer des notions de 5e en 6e.
Il faut prévoir pour chaque leçon 2 niveaux : basique et avancé.
En effet il y aura beaucoup d'heures dédoublées à cause de la marge.
Il faut donc faire les même notions à deux niveaux différents d'approfondissement.
Par exemple : avec le groupe des bons en maths tu fais la preuve et avec l'autre groupe seulement l'entraînement basique.
On peut ainsi voir certaines techniques avancées avec un groupe et pas l'autre.
Je n'ai pas le temps là, mais je vais te donner ma propre idée de progression.
Il faut encore que je compile mes sources, tout n'est pas prêt.
Peux-tu mettre ta progression en texte pour qu'on puisse commenter simplement (l'image c'est pas pratique) ?
 OmbredeloupNiveau 7
OmbredeloupNiveau 7
J'ai l'impression de débarquer d'une autre planète quand je vois tes propositions de progression pour l'an prochain.
Il faut dire que je suis de la "nouvelle" génération. J'ai l'impression qu'avec les 3,5h que l'on nous concède pour le cycle 4, mes élèves qui en 4e, me font encore des erreurs du type " Le double de 2,9 est 4,18 ", je ne ferai que "noyer" les plus faibles.
Evidemment, c'est très intéressant, et je suis très impressionnée que vous puissiez tous transmettre ça à vos élèves. Est-ce qu'il serait possible, à titre indicatif, que vous donniez le temps passé sur les notions ?
Il faut dire que je suis de la "nouvelle" génération. J'ai l'impression qu'avec les 3,5h que l'on nous concède pour le cycle 4, mes élèves qui en 4e, me font encore des erreurs du type " Le double de 2,9 est 4,18 ", je ne ferai que "noyer" les plus faibles.
Evidemment, c'est très intéressant, et je suis très impressionnée que vous puissiez tous transmettre ça à vos élèves. Est-ce qu'il serait possible, à titre indicatif, que vous donniez le temps passé sur les notions ?
 Pat BÉrudit
Pat BÉrudit
pailleauquebec a écrit:Mon sentiment : (je ne détiens pas la vérité)
Je pense qu'il faut impérativement charger plus le niveau sixième qui aura 4h30 et faire une progression 6 5 4 3. Il faut déplacer des notions de 5e en 6e.
Il faut prévoir pour chaque leçon 2 niveaux : basique et avancé.
En effet il y aura beaucoup d'heures dédoublées à cause de la marge.
Il faut donc faire les même notions à deux niveaux différents d'approfondissement.
Par exemple : avec le groupe des bons en maths tu fais la preuve et avec l'autre groupe seulement l'entraînement basique.
On peut ainsi voir certaines techniques avancées avec un groupe et pas l'autre.
Je n'ai pas le temps là, mais je vais te donner ma propre idée de progression.
Il faut encore que je compile mes sources, tout n'est pas prêt.
Peux-tu mettre ta progression en texte pour qu'on puisse commenter simplement (l'image c'est pas pratique) ?
C'est beau de rêver. Heures de marges ? Celles qui vont se réduire très vite au fil des ans ? (d'après ce que le recteur a dit à mon cde...). Pour l'an prochain, j'ai quémandé à mon chef 3 classes à 4h en 4ème-3ème, en prenant pour chaque classe 1/2h de marge pour dédoubler et différencier, AP, etc... Il a refusé. J'ai 4 classes à 3h30, point barre. Et pas d'accès à la salle informatique, vraisemblablement. Tout va bien...
(et ayant des élèves plutôt en grande difficulté, je sais aussi que pour moi, les objectifs affichés par Ycombe ne sont pas atteignables, pas par 80% de mes élèves... j'aurais bien voulu essayer de les atteindre avec les autres, mais je ne pourrai pas)
Page 1 sur 4 • 1, 2, 3, 4 

- Progression détaillée mathématiques Cycle 4 5eme nouveaux programmes 2016
- Progression détaillée mathématiques Cycle 3 6eme nouveaux programmes 2016
- Progression détaillée mathématiques Cycle 4 3eme nouveaux programmes 2016
- Progression détaillée mathématiques Cycle 4 4eme nouveaux programmes 2016
- Mathématiques Cycle 3/Cycle 4 : Sesamath vs Iparcours
Permission de ce forum:
Vous ne pouvez pas répondre aux sujets dans ce forum



