- AndréCNiveau 9
Balthazaard a écrit:AndréC a écrit:Verdurette a écrit:
Tout à fait, la grande majorité des problèmes vient de la non compréhension de la langue.
Faudrait quand même pas trop pousser....
1*x=x
0*x=0
0.5=1/2
x+x=2x et non pas x²
2*(3+1)=2*3+2*1 mais pas 2*3+1 (parenthèse facultative..!!)
.
etc
La liste est longue de ces petites évidences à acquérir qui bloquent tous les calculs et empêchent la moindre efficacité. Le propos est faussement consensuel et , à mon avis militant. La raison PRINCIPALE de l'inefficacité des élèves dans la résolution de problème est le manque de technique de base et de familiarité avec les mécanismes élémentaires du calcul.
La familiarité est une condition nécessaire, mais pas suffisante.
 InvitéInvité
InvitéInvité
J'ai travaillé un temps à la conception d'exercices pour les évaluations nationales ainsi que pour une collection édité par le CRDP du Nord-Pas-De-Calais. On nous avait demandé (demande émanant de la DEPP pour les évaluations nationales) de produire des énoncés clairs et concis. C'est ce que j'essaie de faire désormais dans ma pratique quotidienne : des phrases courtes pour chaque information, report à la ligne systématique pour toute nouvelle information. Police de caractères lisible. Nombres écrits en chiffres. Exemple :André C a écrit:
Verdurette a écrit:
Je ne sais pas ce qu'en penseront les professeurs de collège et de lycée, mais je trouve, à mon échelle, que les élèves achoppent sur les mathématiques plus pour des raisons de non-compréhension linguistique, sémantique, de l'énoncé que pour des raisons purement mathématiques.
Et si, il y a aussi un déficit en calcul.
Tout à fait, la grande majorité des problèmes vient de la non compréhension de la langue.
Zoé ne collectionne que des timbres français, anglais et espagnols.
10 % des timbres de sa collection sont espagnols.
30 % de ses timbres sont anglais.
Elle possède 150 timbres français.
Quel est le nombre total de timbres de sa collection ?
J'ajoute qu'on peut poser des problèmes intéressants sans avoir recours à la langue.
Exemple :
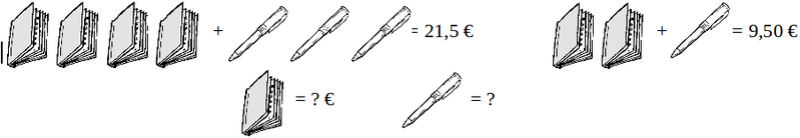
 VerduretteModérateur
VerduretteModérateur
Mais je n'évoquais même pas des énoncés complexes ou mal écrits.
Je parle de termes simples , par exemple : 6 tables avec 4 chaises chacune ... certains n'ont pas compris que chaque table était entourée de 4 chaises.
Je parle de termes simples , par exemple : 6 tables avec 4 chaises chacune ... certains n'ont pas compris que chaque table était entourée de 4 chaises.
 BalthazaardVénérable
BalthazaardVénérable
AndréC a écrit:Balthazaard a écrit:AndréC a écrit:Verdurette a écrit:
Tout à fait, la grande majorité des problèmes vient de la non compréhension de la langue.
Faudrait quand même pas trop pousser....
1*x=x
0*x=0
0.5=1/2
x+x=2x et non pas x²
2*(3+1)=2*3+2*1 mais pas 2*3+1 (parenthèse facultative..!!)
.
etc
La liste est longue de ces petites évidences à acquérir qui bloquent tous les calculs et empêchent la moindre efficacité. Le propos est faussement consensuel et , à mon avis militant. La raison PRINCIPALE de l'inefficacité des élèves dans la résolution de problème est le manque de technique de base et de familiarité avec les mécanismes élémentaires du calcul.
La familiarité est une condition nécessaire, mais pas suffisante.
je ne dis rien d'autre il me semble , mais à moins que la langue ne pose aussi des problèmes aux profs de maths, cause n'est pas synonyme de condition. Ni d'ailleurs que la validité d'un énoncé implique celle de sa réciproque.
 BoubouleDoyen
BoubouleDoyen
Examen de physique à bac+1 tout frais.
Evolution en fonction de la température pour débuter le problème :
ln(P) = a/T-b avec a et b deux constantes.
Le quart de la promotion a calculé comme ln(P) = a/(T-b). Problème foiré dès le départ.
La prochaine fois le physicien écrira mieux, soit en éditant l'équation avec un trait de fraction horizontal, soit en écrivant ln(P) = -b + a/T.
Evolution en fonction de la température pour débuter le problème :
ln(P) = a/T-b avec a et b deux constantes.
Le quart de la promotion a calculé comme ln(P) = a/(T-b). Problème foiré dès le départ.
La prochaine fois le physicien écrira mieux, soit en éditant l'équation avec un trait de fraction horizontal, soit en écrivant ln(P) = -b + a/T.
 JPhMMDemi-dieu
JPhMMDemi-dieu
La langue française, c'est le mal.
Deux droites et une droite sécante aux deux premières. Les points qui vont bien sur les droites.
"Écrire un couple d'angles correspondants. Écrire un couple d'angles alternes-internes.
- Ça fait quatre angles m'sieur !
- Ou trois."
Stupéfaction dans la salle.
Conclusion : la langue française, c'est le mal. A moins que ce soit autre chose.
Deux droites et une droite sécante aux deux premières. Les points qui vont bien sur les droites.
"Écrire un couple d'angles correspondants. Écrire un couple d'angles alternes-internes.
- Ça fait quatre angles m'sieur !
- Ou trois."
Stupéfaction dans la salle.
Conclusion : la langue française, c'est le mal. A moins que ce soit autre chose.
_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
 InvitéInvité
InvitéInvité
Bouboule a écrit:Examen de physique à bac+1 tout frais.
Evolution en fonction de la température pour débuter le problème :
ln(P) = a/T-b avec a et b deux constantes.
Le quart de la promotion a calculé comme ln(P) = a/(T-b). Problème foiré dès le départ.
La prochaine fois le physicien écrira mieux, soit en éditant l'équation avec un trait de fraction horizontal, soit en écrivant ln(P) = -b + a/T.
Tu veux dire évolution de la pression en fonction de la température ?

Cela me fait penser que j'enrage quand certains de mes élèves disent "C'est proportionnel".
Je leur dis que cette phrase n'a pas de sens ! Pour moi, il faut préciser quelle grandeur est proportionnelle à quelle autre grandeur.
Avec ln(P) = b + a/T ils risquent de comprendre (b+a)/T
De façon générale, en ce qui me concerne, le slash j'évite....
 InvitéInvité
InvitéInvité
Pour moi, c'est autre chose dans ce cas.JPhMM a écrit:La langue française, c'est le mal.
Deux droites et une droite sécantes aux deux premières. Les points qui vont bien sur les droites.
"Écrire un couple d'angles correspondants. Écrire un couple d'angles alternes-internes.
- Ça fait quatre angles m'sieur !
- Ou trois."
Stupéfaction dans la salle.
Conclusion : la langue française, c'est le mal. A moins que ce soit autre chose.
Et cette autre chose est ici très intéressant...
 JPhMMDemi-dieu
JPhMMDemi-dieu
Je songe que les responsabilités sont partagées entre la langue et cette autre chose, et oui, je trouve aussi cela très intéressant.Franck059 a écrit:Pour moi, c'est autre chose dans ce cas.JPhMM a écrit:La langue française, c'est le mal.
Deux droites et une droite sécantes aux deux premières. Les points qui vont bien sur les droites.
"Écrire un couple d'angles correspondants. Écrire un couple d'angles alternes-internes.
- Ça fait quatre angles m'sieur !
- Ou trois."
Stupéfaction dans la salle.
Conclusion : la langue française, c'est le mal. A moins que ce soit autre chose.
Et cette autre chose est ici très intéressant...
_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
 InvitéInvité
InvitéInvité
Verdurette a écrit:Mais je n'évoquais même pas des énoncés complexes ou mal écrits.
Je parle de termes simples , par exemple : 6 tables avec 4 chaises chacune ... certains n'ont pas compris que chaque table était entourée de 4 chaises.
Et :
"On considère 6 tables, chacune étant entourée de 4 chaises ?"
Un adulte pourrait penser que je chipote, mais un enfant....
 amalricuNeoprof expérimenté
amalricuNeoprof expérimenté
Balthazaard a écrit:AndréC a écrit:Balthazaard a écrit:AndréC a écrit:
Faudrait quand même pas trop pousser....
1*x=x
0*x=0
0.5=1/2
x+x=2x et non pas x²
2*(3+1)=2*3+2*1 mais pas 2*3+1 (parenthèse facultative..!!)
.
etc
La liste est longue de ces petites évidences à acquérir qui bloquent tous les calculs et empêchent la moindre efficacité. Le propos est faussement consensuel et , à mon avis militant. La raison PRINCIPALE de l'inefficacité des élèves dans la résolution de problème est le manque de technique de base et de familiarité avec les mécanismes élémentaires du calcul.
La familiarité est une condition nécessaire, mais pas suffisante.
je ne dis rien d'autre il me semble , mais à moins que la langue ne pose aussi des problèmes aux profs de maths, cause n'est pas synonyme de condition. Ni d'ailleurs que la validité d'un énoncé implique celle de sa réciproque.
Le professeur de mathématiques de mon fils a écrit "peu de motivation expliquent ces résultats...", je sais c'est mesquin, mais personne n'est parfait.
Pour moi le rescapé des sciences, j'ai toujours ressenti qu'il y a avait une part d'implicite dans beaucoup d'énoncés et que faute de le percevoir on allait à l'échec. J'ai alors laissé tomber sans vergogne considérant que ce n'était pas mon monde et depuis je m'en porte bien mieux. L'intelligence mathématique requiert des dispositions que j'ignore et même en travaillant d'arrache-pied, je reste interdit et besogneux devant certains énoncés alors que leurs auteurs ne voient pas de problème d'énonciation comme si tout allait de soi. Ce quant-à-soi éloigne et rebute bien des élèves et/ou des parents.
 JPhMMDemi-dieu
JPhMMDemi-dieu
De nombreux énoncés sont aussi peu clairs. Sésamath en est truffé, par exemple.Franck059 a écrit:Verdurette a écrit:Mais je n'évoquais même pas des énoncés complexes ou mal écrits.
Je parle de termes simples , par exemple : 6 tables avec 4 chaises chacune ... certains n'ont pas compris que chaque table était entourée de 4 chaises.
Et :
"On considère 6 tables, chacune étant entourée de 4 chaises ?"
Un adulte pourrait penser que je chipote, mais un enfant....
_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
 JPhMMDemi-dieu
JPhMMDemi-dieu
Il y a presque toujours une part d'implicite.amalricu a écrit:Pour moi le rescapé des sciences, j'ai toujours ressenti qu'il y a avait une part d'implicite dans beaucoup d'énoncés
Un exemple très simple :
"Calculer 516:12"
Une réponse tout à fait valable (pour ne pas dire qu'elle est "plus" valable que tout autre) est 516/12.
_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
 InvitéInvité
InvitéInvité
Verdurette a écrit:
(J'ai essayé la méthode de Singapour, mais quand elle n'est pas utilisée dès le départ, en CP, et qu'elle est introduite ponctuellement, alors que les autres classes ne la pratiquent pas, c'est contre-productif. J'ai renoncé. Et si vous avez des conseils je suis preneuse. )
Je pense que la méthode de Singapour est très intéressante, notamment pour TOUT ce qu'elle implique :
- Construction des apprentissages progressifs du CP au CM2 (donc effectivement ne l'appliquer que dans un niveau, ça la fout mal...) avec apparition des même thèmes d'une année sur l'autre, lesquels sont davantage approfondis quand on monte en grade.
- Passage de la manipulation à l'imagé puis à l'abstraction
- Pédagogie explicite
- Paliers de révisions reprenant les trois ou quatre derniers thèmes enseignés
- Illustration sobre des ouvrages
Et dans certains pays : ouvrages nombreux (livres de cours + livres d'exercices + livres de remédiation + livres d'approfondissement + livres d'évaluations)
 Marc au PoloNiveau 2
Marc au PoloNiveau 2
JPhMM a écrit:
Il y a presque toujours une part d'implicite.
"Calculer 516:12"
Dans quelle base?

 amalricuNeoprof expérimenté
amalricuNeoprof expérimenté
Marc au Polo a écrit:JPhMM a écrit:
Il y a presque toujours une part d'implicite.
"Calculer 516:12"
Dans quelle base?
C'est bien ce que je disais...
La part d'implicite est réelle dans certains énoncés alors quand on balance un attendu mathématique contextualisé (cf l'âge du capitaine), on ajoute un nouveau filtre, un implicite supplémentaire et énigmatique. On perd des gens pour moins que ça.
 JPhMMDemi-dieu
JPhMMDemi-dieu
Aussi.Marc au Polo a écrit:JPhMM a écrit:
Il y a presque toujours une part d'implicite.
"Calculer 516:12"
Dans quelle base?
_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
 JPhMMDemi-dieu
JPhMMDemi-dieu
Et nous plussoyions...amalricu a écrit:Marc au Polo a écrit:JPhMM a écrit:
Il y a presque toujours une part d'implicite.
"Calculer 516:12"
Dans quelle base?
C'est bien ce que je disais...
_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
 BalthazaardVénérable
BalthazaardVénérable
Bouboule a écrit:Examen de physique à bac+1 tout frais.
Evolution en fonction de la température pour débuter le problème :
ln(P) = a/T-b avec a et b deux constantes.
Le quart de la promotion a calculé comme ln(P) = a/(T-b). Problème foiré dès le départ.
La prochaine fois le physicien écrira mieux, soit en éditant l'équation avec un trait de fraction horizontal, soit en écrivant ln(P) = -b + a/T.
Vrai problème, mes élèves n'écrivent plus de parenthèses, ce qui ne veut pas forcément dire qu'ils en ignorent l'usage. Ce n'é pa la péne come l'otrografe dayeur puisquon conpren.
Tout le monde fait un jour ou l'autre une faute d'orthographe (il y a en a peut-être là) ou de grammaire, mais entre une étourderie et un mépris ou une ignorance des règles il y a du chemin.
Une fois confrontés à une situation où elles (ou leur absence) sont nécessaires le mal arrive.
Est-ce au prof de suppléer à la chose en évitant les cas ambigus? je ne pense pas.
 AndréCNiveau 9
AndréCNiveau 9
Balthazaard a écrit:AndréC a écrit:Balthazaard a écrit:
Faudrait quand même pas trop pousser....
1*x=x
0*x=0
0.5=1/2
x+x=2x et non pas x²
2*(3+1)=2*3+2*1 mais pas 2*3+1 (parenthèse facultative..!!)
.
etc
La liste est longue de ces petites évidences à acquérir qui bloquent tous les calculs et empêchent la moindre efficacité. Le propos est faussement consensuel et , à mon avis militant. La raison PRINCIPALE de l'inefficacité des élèves dans la résolution de problème est le manque de technique de base et de familiarité avec les mécanismes élémentaires du calcul.
La familiarité est une condition nécessaire, mais pas suffisante.
je ne dis rien d'autre il me semble , mais à moins que la langue ne pose aussi des problèmes aux profs de maths, cause n'est pas synonyme de condition. Ni d'ailleurs que la validité d'un énoncé implique celle de sa réciproque.
Vous dites LA (raison principale) ce qui signifie que les autres sont accessoires, je dis UNE sans hiérarchiser.
 JPhMMDemi-dieu
JPhMMDemi-dieu
Je crois que peu parmi les responsables français ont essayé de mettre le doigt sur le fait qui expliquerait pourquoi nous en sommes arrivés là. Sans doute se dérobe-t-il à leur analyse. Sans doute est-il plus profond qu'ils ne veulent nous le faire croire. Sans doute touche-t-il à quelque chose de grand que l'enseignement lui-même des mathématiques. La place des mathématiques dans la culture française ? Son évolution ? L'évolution de la place des mathématiques dans la culture internationale et sa non évolution dans la culture française ? ou une évolution en sens opposé ?
Combien de hurlements parmi eux si on leur disait que les mathématiques sont une des branches culturelles les plus riches, profondes, anciennes, pénétrantes, prometteuses, de l'histoire de l'humanité ? Et si le monde n'était pas mathématique ? Et si c'était la culture humaine qui était mathématique, autant que littéraire, ou artistique, ou philosophique ?
Combien de hurlements parmi eux si on disait que les mathématiques ne sont pas un ensemble de règles et de recettes et de méthodes et de compétences ?
Certains pays ont réalisé ce qui est en train de se passer, et ont décidé de se donner les moyens de ne pas rater le coche, en se donnant pour objectif de donner à leurs nouvelles générations un bagage culturel mathématique maximal. Pendant ce temps, la France décidait de donner à ses nouvelles générations un socle, ce qui est, stricto sensu, un bagage minimal. Folie française. Nous mettrons beaucoup de temps à nous relever des conséquences de cette folie-là.
Combien de hurlements parmi eux si on leur disait que les mathématiques sont une des branches culturelles les plus riches, profondes, anciennes, pénétrantes, prometteuses, de l'histoire de l'humanité ? Et si le monde n'était pas mathématique ? Et si c'était la culture humaine qui était mathématique, autant que littéraire, ou artistique, ou philosophique ?
Combien de hurlements parmi eux si on disait que les mathématiques ne sont pas un ensemble de règles et de recettes et de méthodes et de compétences ?
Certains pays ont réalisé ce qui est en train de se passer, et ont décidé de se donner les moyens de ne pas rater le coche, en se donnant pour objectif de donner à leurs nouvelles générations un bagage culturel mathématique maximal. Pendant ce temps, la France décidait de donner à ses nouvelles générations un socle, ce qui est, stricto sensu, un bagage minimal. Folie française. Nous mettrons beaucoup de temps à nous relever des conséquences de cette folie-là.
_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
 ycombeMonarque
ycombeMonarque
Ce que je crains avec la mission Torossian-Villani: qu'on fasse une "Singapour" à la française, en gardant manipulation/imagé/abstrait mais sans garder le côté pédagogie explicite. Pour moi ça serait continuer dans l'échec.Franck059 a écrit:Verdurette a écrit:
(J'ai essayé la méthode de Singapour, mais quand elle n'est pas utilisée dès le départ, en CP, et qu'elle est introduite ponctuellement, alors que les autres classes ne la pratiquent pas, c'est contre-productif. J'ai renoncé. Et si vous avez des conseils je suis preneuse. )
Je pense que la méthode de Singapour est très intéressante, notamment pour TOUT ce qu'elle implique :
- Construction des apprentissages progressifs du CP au CM2 (donc effectivement ne l'appliquer que dans un niveau, ça la fout mal...) avec apparition des même thèmes d'une année sur l'autre, lesquels sont davantage approfondis quand on monte en grade.
- Passage de la manipulation à l'imagé puis à l'abstraction
- Pédagogie explicite
[...]
_________________
Assurbanipal: "Passant, mange, bois, divertis-toi ; tout le reste n’est rien".
Franck Ramus : "Les sciences de l'éducation à la française se font fort de produire un discours savant sur l'éducation, mais ce serait visiblement trop leur demander que de mettre leur discours à l'épreuve des faits".
 BoubouleDoyen
BoubouleDoyen
Franck059 a écrit:Bouboule a écrit:Examen de physique à bac+1 tout frais.
Evolution en fonction de la température pour débuter le problème :
ln(P) = a/T-b avec a et b deux constantes.
Le quart de la promotion a calculé comme ln(P) = a/(T-b). Problème foiré dès le départ.
La prochaine fois le physicien écrira mieux, soit en éditant l'équation avec un trait de fraction horizontal, soit en écrivant ln(P) = -b + a/T.
Tu veux dire évolution de la pression en fonction de la température ?
Cela me fait penser que j'enrage quand certains de mes élèves disent "C'est proportionnel".
Je leur dis que cette phrase n'a pas de sens ! Pour moi, il faut préciser quelle grandeur est proportionnelle à quelle autre grandeur.
Avec ln(P) = b + a/T ils risquent de comprendre (b+a)/T
De façon générale, en ce qui me concerne, le slash j'évite....
Je reçois bien toutes les nuances exprimées (et c'est d'ailleurs là qu'on peut admirer combien les sujets de bac sont calibrés pour éviter ce genre de catastrophe, enfin la plupart du temps).
Avec ln(P) = b+a/T, je pense qu'il y aurait moins d'erreur voire pas car a et b étaient des nombres donc ils n'auront pas l'idée de les additionner mais le test serait intéressant à faire.
Tu as raison d'éviter le slash mais je suppose que vu que c'était l'examen, il y avait déjà une certaine culture à la fois sur le phénomène et sur la façon dont le prof tape ses énoncés. Trouver P aberrant aurait aussi dû surprendre. Cela rejoint les fameux implicites évoqués. Les énoncés sont effectivement souvent implicites dans leur rédaction mais il y a toute une base qui est travaillée dans le cours et les exos avant l'examen.
Enfin, la calculette était autorisée, il suffisait de taper l'application numérique comme c'était écrit en remplaçant T par la valeur (il fallait juste calculer P à deux températures).
Bref...
 VerduretteModérateur
VerduretteModérateur
Franck059 a écrit:Je pense que la méthode de Singapour est très intéressante, notamment pour TOUT ce qu'elle implique :
- Construction des apprentissages progressifs du CP au CM2 (donc effectivement ne l'appliquer que dans un niveau, ça la fout mal...) avec apparition des même thèmes d'une année sur l'autre, lesquels sont davantage approfondis quand on monte en grade.
- Passage de la manipulation à l'imagé puis à l'abstraction
- Pédagogie explicite
- Paliers de révisions reprenant les trois ou quatre derniers thèmes enseignés
- Illustration sobre des ouvrages
Et dans certains pays : ouvrages nombreux (livres de cours + livres d'exercices + livres de remédiation + livres d'approfondissement + livres d'évaluations)
Je suis tout à fait d'accord, et c'est bien ce que je disais, il faut qu'elle soit utilisée d'une classe à l'autre. Débuter en CE2, avec, en plus, un décloisonnement hebdomadaire par niveau, c'est juste impossible. Je l'ai utilisée antérieurement, et je la garde sous le coude.
Deux remarques :
1/ La nouvelle édition "programmes 2016" comporte ces fameux "calculs" sur bande numérique (avancer pour additionner, reculer pour soustraire) que je ne cautionne pas. Il leur a fallu avaler quelques couleuvres, je pense, pour obtenir cet imprimatur ministériel, et ce n'est peut-être pas ce qu'ils ont fait de mieux. Enfin, sur un plan commercial, peut-être, sur celui de l'éthique pédagogique, j'en suis moins sûre.
2/ On peut toujours transposer les exigences de raisonnement verbal à une autre méthode.
 BrindIfFidèle du forum
BrindIfFidèle du forum
J'ai découvert ça cette annéeBalthazaard a écrit:Vrai problème, mes élèves n'écrivent plus de parenthèses, ce qui ne veut pas forcément dire qu'ils en ignorent l'usage.

Certains les gardent dans leur tête, puisqu'à la ligne de calcul suivante la distribution est faite correctement. C'est très surprenant. L'économie d'encre ne me parait pas valoir le surcroît de concentration exigée

un élève de 2de a écrit:A=5x-(x+1)²
A=5x-x²+2x+1
A=-x²+3x-1
Et bien sûr d'autres élèves se contente de les supprimer de leur copie et de leur mémoire, ce qui fausse leurs calculs. Et si les premiers expliquent aux seconds en quoi ils se sont trompés, ça ne va pas aider à les convaincre qu'avec du travail et de la rigueur ils pourraient parvenir à faire les exercices donnés.
 BrindIfFidèle du forum
BrindIfFidèle du forum
En 1re, notre professeur de Français nous avait expliqué que grammaticalement, « un chien a trois pattes » n'en avait effectivement que trois. Même si mathématiquement la plupart des chiens peuvent être décrits comme ayant trois pattes. L'exemple m'a marquée, mais j'ai oublié le nom du truc de grammaire qui décrit cette subtilitéJPhMM a écrit:Je songe que les responsabilités sont partagées entre la langue et cette autre chose, et oui, je trouve aussi cela très intéressant.Franck059 a écrit:Pour moi, c'est autre chose dans ce cas.JPhMM a écrit:Conclusion : la langue française, c'est le mal. A moins que ce soit autre chose.
Et cette autre chose est ici très intéressant...
Il y a aussi le mot « ou » qui en français a un sens logique dépendant du contexte, et qui vaut la peine d'y revenir encore et encore avec les élèves. « Si vos parents vous promettent un nouveau smartphone si vous avez des bonnes notes en maths ou en physique, et que vous avez des bonnes notes dans les deux matières, que se passe-t-il ? »

Permission de ce forum:
Vous ne pouvez pas répondre aux sujets dans ce forum




