Page 1 sur 2 • 1, 2 

 moi020Niveau 1
moi020Niveau 1
Bonjour à tous,
enseignante titulaire au collège depuis à peine 1 an, je vais être inspectée jeudi. Cela tombera normalement dans ma progression lors de ma deuxième séance sur les statistiques. Je ne sais pas trop où j'en serai rendue avec les définitions médiane, quartiles, étendue et ne sais pas trop comment gérer ma séance. Je pense faire comme habituellement les activités rapides de 10 min au rétro avec 5 questions de calcul/géométrie mentale, corriger l'exercice à faire pour la séance mais après ? Un exercice de révision de 4ème sur les diagrammes, une activité de recherche ? Je remercie toute personne d'avance pour son aide ! Une néotit en panique !
enseignante titulaire au collège depuis à peine 1 an, je vais être inspectée jeudi. Cela tombera normalement dans ma progression lors de ma deuxième séance sur les statistiques. Je ne sais pas trop où j'en serai rendue avec les définitions médiane, quartiles, étendue et ne sais pas trop comment gérer ma séance. Je pense faire comme habituellement les activités rapides de 10 min au rétro avec 5 questions de calcul/géométrie mentale, corriger l'exercice à faire pour la séance mais après ? Un exercice de révision de 4ème sur les diagrammes, une activité de recherche ? Je remercie toute personne d'avance pour son aide ! Une néotit en panique !
 JPhMMDemi-dieu
JPhMMDemi-dieu
Introduire une nouvelle notion me semble un minimum pour une inspection. Mais ce n'est qu'un avis personnel.
_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
 marie91270Neoprof expérimenté
marie91270Neoprof expérimenté
JPhMM a écrit:Introduire une nouvelle notion me semble un minimum pour une inspection. Mais ce n'est qu'un avis personnel.
Pas nécessairement : je n'ai introduit aucune nouvelle notion lors de mon inspection il y a 2 ans et j'ai eu un excellent rapport (travail de groupes avec des tâches complexes, tout ce qu'aiment les IPR!)
Voici une tâche complexe sur les stats que je pense proposer à mes 4ème en fin d'année. Je pense que si je tombais sur les stats lors d'une inspection, c'est un truc de ce style que je ferais.
L'activité n'est pas de moi, elle est issue du nouveau transmath 4ème.

 moi020Niveau 1
moi020Niveau 1
Merci pour vos réponses ! C'est une très bonne idée marie91270, mais faire une tâche complexe en inspection ne me rassure pas trop et je ne saurais pas si je dois la mener en individuel ou en groupe. J'aimerais un exercice de 4ème un peu ouvert mais peut être pas autant ^^. Ce n'est pas évident de trouver le juste milieu. En tout cas je la retiens !
 fifi51Fidèle du forum
fifi51Fidèle du forum
Bonjour;
je donne mon avis en tant que statisticien, je trouve les diagrammes circulaires relativement incompréhensibles (en ce sens où il me faut à tout moment regarder la légende pour lire le diagramme).
Après, je dirais qu'au delà des définitions, ce qui me semble important (et en supposant que la notion de moyenne ait été abordée), c'est de montrer les limites de la moyenne et de la médiane et leurs intêrets respectifs. Eventuellement (un peu sur le mode journalistique), faire travailler les élèves sur un même jeu de données (tirées de la vie réelle et parlant pour les élèves, à chaud sans trop réfléchir, je dirais: la taille des élèves, une distribution de salaire avec Bill Gates dans l'échantillon, et un devoir où près de la moitié des élèves a très bien compris et l'autre moitié quasiment pas ), d'un côté avec médiane et quartiles et de l'autre avec la moyenne et demander les conclusions qu'ils en tirent à l'aide des indicateurs calculés, voire les conclusions sans les calculs (id est leur opinion).
En résumé, ce qui me paraît important c'est:
_ Savoir calculer ces indicateurs
_ "comprendre" ce qui est calculé à l'aide de ces indicateurs.
Mais, je ne suis pas professeur de mathématiques et je ne sais absolument pas ce qu'on attend en ce domaine d'un élève de 4ème.
je donne mon avis en tant que statisticien, je trouve les diagrammes circulaires relativement incompréhensibles (en ce sens où il me faut à tout moment regarder la légende pour lire le diagramme).
Après, je dirais qu'au delà des définitions, ce qui me semble important (et en supposant que la notion de moyenne ait été abordée), c'est de montrer les limites de la moyenne et de la médiane et leurs intêrets respectifs. Eventuellement (un peu sur le mode journalistique), faire travailler les élèves sur un même jeu de données (tirées de la vie réelle et parlant pour les élèves, à chaud sans trop réfléchir, je dirais: la taille des élèves, une distribution de salaire avec Bill Gates dans l'échantillon, et un devoir où près de la moitié des élèves a très bien compris et l'autre moitié quasiment pas ), d'un côté avec médiane et quartiles et de l'autre avec la moyenne et demander les conclusions qu'ils en tirent à l'aide des indicateurs calculés, voire les conclusions sans les calculs (id est leur opinion).
En résumé, ce qui me paraît important c'est:
_ Savoir calculer ces indicateurs
_ "comprendre" ce qui est calculé à l'aide de ces indicateurs.
Mais, je ne suis pas professeur de mathématiques et je ne sais absolument pas ce qu'on attend en ce domaine d'un élève de 4ème.
_________________
Oui, j'ai un clavier Fisher Price pour l'instant !
 t3-Niveau 5
t3-Niveau 5
Petit détail de rigueur, fais attention à la définition de médiane. (D'ailleurs, faut-il donner une définition ?)
J'ai tenté cette année :
Définition. On appelle médiane d'une série statistique un nombre $m$ tel que:
- au moins la moitié des valeurs de la série sont inférieures ou égales à $m$ ;
- au moins la moitié des valeurs de la série sont supérieures ou égales à $m$.
Mais je me suis aperçu que cette définition ne convient pas.
Par exemple, pour la série : 1 ; 2 ; 3 ; 4
2 convient pour médiane avec la définition ci-dessus, et ce n'est pas ce qu'on souhaite.
Le site euler, de l'inspection de maths de l'académie de Versailles, propose : http://euler.ac-versailles.fr/baseeuler/lexique/notion.jsp?id=21 à niveau troisième !! Cela ne me semble vraiment pas réaliste de donner cette définition à des troisièmes... Je n'ai pas trouvé le moyen d'éviter les indices des nombres tout en restant rigoureux
Il reste le pas très rigoureux "qui partage en deux séries de même effectif" de pas mal de manuels... ou ne pas donner de définitions du tout et se contenter d'exemples.
Je ne sais pas ce que je choisirai l'an prochain... Des idées chers collègues ?
J'ai tenté cette année :
- au moins la moitié des valeurs de la série sont inférieures ou égales à $m$ ;
- au moins la moitié des valeurs de la série sont supérieures ou égales à $m$.
Mais je me suis aperçu que cette définition ne convient pas.
Par exemple, pour la série : 1 ; 2 ; 3 ; 4
2 convient pour médiane avec la définition ci-dessus, et ce n'est pas ce qu'on souhaite.
Le site euler, de l'inspection de maths de l'académie de Versailles, propose : http://euler.ac-versailles.fr/baseeuler/lexique/notion.jsp?id=21 à niveau troisième !! Cela ne me semble vraiment pas réaliste de donner cette définition à des troisièmes... Je n'ai pas trouvé le moyen d'éviter les indices des nombres tout en restant rigoureux
Il reste le pas très rigoureux "qui partage en deux séries de même effectif" de pas mal de manuels... ou ne pas donner de définitions du tout et se contenter d'exemples.
Je ne sais pas ce que je choisirai l'an prochain... Des idées chers collègues ?
 ChmickNiveau 2
ChmickNiveau 2
Après avoir diagnostiqué le peu de connaissances sur ce sujet de mes élèves de 3ème cette année.
Nous sommes allés au CDI, je les ai mis en groupe et leur consigne était de me présenter de la façon dont ils le désiraient le chapitre stat vu en 4ème en y intégrant des exemples (à refaire si possible) et des définitions...
Ils avaient la possibilité de prendre des manuels scolaires de 5ème et 4ème et avaient un accès internet.
Ils pouvaient présenter comme ils le souhaitaient : Cours classique, carte mentale, diaporama...
Nous sommes allés au CDI, je les ai mis en groupe et leur consigne était de me présenter de la façon dont ils le désiraient le chapitre stat vu en 4ème en y intégrant des exemples (à refaire si possible) et des définitions...
Ils avaient la possibilité de prendre des manuels scolaires de 5ème et 4ème et avaient un accès internet.
Ils pouvaient présenter comme ils le souhaitaient : Cours classique, carte mentale, diaporama...
 SandyVegNiveau 9
SandyVegNiveau 9
Bonjour,
Voici l'activité que j'utilise pour introduire les quartiles.
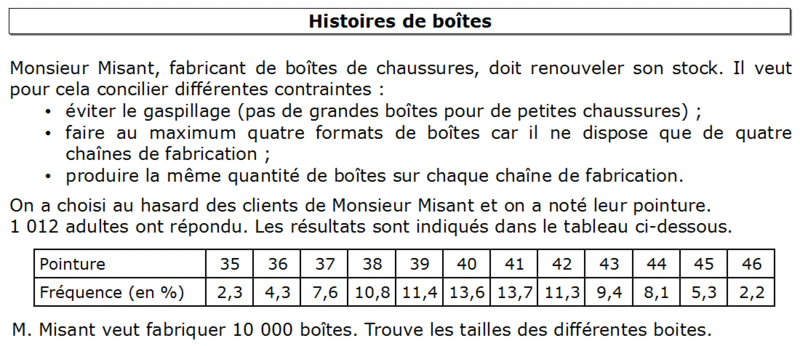
Voici l'activité que j'utilise pour introduire les quartiles.

_________________
- Parcours :
- Enseignante spécialisée
2017-2019 : T5 & T6 - Coordonnatrice d'un dispositif ULIS collège + formation CAPPEI.
Prof de maths
2015-2017 : T3 & T4 - Classes de 6e et de 3e - PP 6e + coordo Maths + coordo 6e
2014-2015 : T2 - Classes de 5e et de 4e
2013-2014 : T1 - Classes de 5e, 4e, 3e, 2nde et 1ère
2012-2013 : Stagiaire - Classes de 4e et de 3e
2012 : 3e concours du CAPES
2009-2012 : Contractuelle - Plein de petits remplacements en collège et lycée
2005-2012 : Cours particuliers - Collège, lycée et prépa ECE
Informaticienne
2000-2004 : Ingénieur en informatique
1999-2000 : Monitrice d'informatrice à la fac
 BRNiveau 9
BRNiveau 9
t3- a écrit:Petit détail de rigueur, fais attention à la définition de médiane. (D'ailleurs, faut-il donner une définition ?)
J'ai tenté cette année :Définition. On appelle médiane d'une série statistique un nombre $m$ tel que:
- au moins la moitié des valeurs de la série sont inférieures ou égales à $m$ ;
- au moins la moitié des valeurs de la série sont supérieures ou égales à $m$.
Mais je me suis aperçu que cette définition ne convient pas.
Par exemple, pour la série : 1 ; 2 ; 3 ; 4
2 convient pour médiane avec la définition ci-dessus, et ce n'est pas ce qu'on souhaite.
Je serais curieux de savoir ce qu'on souhaite. Dans ton exemple, le nombre 2, le nombre 3 ou le nombre 2,748 sont des médianes au sens de n'importe quelle définition raisonnable d'une valeur médiane.
Dans le cas d'une série de données contenant un nombre pair de données ordonnées de x(1) à x(2n), n'importe quel nombre compris entre x(n) et x(n+1) est une médiane. L'ensemble des valeurs médianes est l'intervalle [x(n),x(n+1)] et, dans ce cas, on convient généralement que la valeur médiane est le milieu ((x(n)+x(n+1))/2 de l'intervalle des valeurs médianes : c'est une convention arbitraire mais raisonnable.
Tu peux noter que l'utilisation de la valeur moyenne ou la valeur médiane a un effet sur l'interprétation des données statistiques qui n'est pas neutre. Je t'invite par exemple à comparer le salaire médian et le salaire moyen en France, et à étudier notamment quelle proportion de salariés ont un salaire supérieur au salaire moyen...
Ainsi on peut trouver facilement une étude de l'INSEE où on apprend que le salaire moyen en 2011 est de 2 130€, alors que le salaire médian est de 1 712€. 40% des salariés gagnent au moins 1 902€, 30% au moins 2 156€. Bref, on peut estimer qu'un peu moins de 70% des salariés gagnent moins que le salaire moyen, et qu'un peu plus de 30% des salariés gagnent plus que le salaire moyen.
Voilà un excellent exercice pour illustrer les notions de moyennes et médianes :-)
Tu peux faire remarquer que la moyenne est facile à calculer : si on reçoit des données en vrac, il suffit de calculer la somme... La médiane est plus difficile à calculer, puisqu'il faut trier les données au préalable. Sans ordinateur, c'est un travail beaucoup plus fastidieux qu'un calcul de somme.
 ycombeMonarque
ycombeMonarque
C'est une des définitions adoptées pour les quartiles. Si la médiane est le quartile du milieu, alors cette définition convient parfaitement.t3- a écrit:Petit détail de rigueur, fais attention à la définition de médiane. (D'ailleurs, faut-il donner une définition ?)
J'ai tenté cette année :Définition. On appelle médiane d'une série statistique un nombre $m$ tel que:
- au moins la moitié des valeurs de la série sont inférieures ou égales à $m$ ;
- au moins la moitié des valeurs de la série sont supérieures ou égales à $m$.
Mais je me suis aperçu que cette définition ne convient pas.
Par exemple, pour la série : 1 ; 2 ; 3 ; 4
2 convient pour médiane avec la définition ci-dessus, et ce n'est pas ce qu'on souhaite.
_________________
Assurbanipal: "Passant, mange, bois, divertis-toi ; tout le reste n’est rien".
Franck Ramus : "Les sciences de l'éducation à la française se font fort de produire un discours savant sur l'éducation, mais ce serait visiblement trop leur demander que de mettre leur discours à l'épreuve des faits".
 ChmickNiveau 2
ChmickNiveau 2
Justement les définitions de médiane et quartiles ne sont pas similaires, en autre le quartile est forcément une valeur de la série contrairement à la médiane dans le cas d'un nombre pair de valeur...
 ycombeMonarque
ycombeMonarque
Non, ça c'est la définition des programmes, qui n'est pas cohérente. Il y a plusieurs définition des quartiles, GNU R en connait une dizaine.Chmick a écrit:Justement les définitions de médiane et quartiles ne sont pas similaires, en autre le quartile est forcément une valeur de la série contrairement à la médiane dans le cas d'un nombre pair de valeur...
La définition des quartiles dans un manuel de statistique pour le supérieur fait correspondre Q2 avec la médiane, en général.
_________________
Assurbanipal: "Passant, mange, bois, divertis-toi ; tout le reste n’est rien".
Franck Ramus : "Les sciences de l'éducation à la française se font fort de produire un discours savant sur l'éducation, mais ce serait visiblement trop leur demander que de mettre leur discours à l'épreuve des faits".
 ChmickNiveau 2
ChmickNiveau 2
ycombe a écrit:Non, ça c'est la définition des programmes, qui n'est pas cohérente. Il y a plusieurs définition des quartiles, GNU R en connait une dizaine.Chmick a écrit:Justement les définitions de médiane et quartiles ne sont pas similaires, en autre le quartile est forcément une valeur de la série contrairement à la médiane dans le cas d'un nombre pair de valeur...
La définition des quartiles dans un manuel de statistique pour le supérieur fait correspondre Q2 avec la médiane, en général.
Oui on est d'accord et c'est justement très embêtant pour la leçon 4ème sans parler du fait que tu ne peux même pas utiliser la fonction quartile d'Excel avec les élèves !
 BrindIfFidèle du forum
BrindIfFidèle du forum
Je ne vois pas trop où est le soucis en fait.
Forcément si on prend un exemple avec 4 valeurs... mais quel est l'intérêt d'une médiane dans ce cas là
Je définis la médiane comme un nombre qui partage la série en deux (définition donnée ci-dessus), et pour le déterminer dans les exercices, j'utilise l'algorithme au programme, à savoir regarder la parité etc.
Si Excel ou la calculatrice fait différemment (il me semble que c'est le plus petit nombre tel que...), c'est l'occasion de réfléchir à l'unicité du résultat d'une définition, voir quelles autres valeurs pourraient être obtenues, bref comprendre un peu mieux, finalement, ce que sont médiane et quartiles et comment ils sont obtenus. Les cas où la médiane est très sensible à la définition choisie sont, me semble-t-il, des cas où ce n'est pas un indicateur approprié.
Forcément si on prend un exemple avec 4 valeurs... mais quel est l'intérêt d'une médiane dans ce cas là

Je définis la médiane comme un nombre qui partage la série en deux (définition donnée ci-dessus), et pour le déterminer dans les exercices, j'utilise l'algorithme au programme, à savoir regarder la parité etc.
Si Excel ou la calculatrice fait différemment (il me semble que c'est le plus petit nombre tel que...), c'est l'occasion de réfléchir à l'unicité du résultat d'une définition, voir quelles autres valeurs pourraient être obtenues, bref comprendre un peu mieux, finalement, ce que sont médiane et quartiles et comment ils sont obtenus. Les cas où la médiane est très sensible à la définition choisie sont, me semble-t-il, des cas où ce n'est pas un indicateur approprié.
 BRNiveau 9
BRNiveau 9
ycombe a écrit:Non, ça c'est la définition des programmes, qui n'est pas cohérente. Il y a plusieurs définition des quartiles, GNU R en connait une dizaine.Chmick a écrit:Justement les définitions de médiane et quartiles ne sont pas similaires, en autre le quartile est forcément une valeur de la série contrairement à la médiane dans le cas d'un nombre pair de valeur...
La définition des quartiles dans un manuel de statistique pour le supérieur fait correspondre Q2 avec la médiane, en général.
Le programme officiel n'impose aucune définition des médianes et quartiles. Seul le document ressource organisation et gestion de données propose une définition des médianes et quartiles. Comme le souligne ycombe, ces définitions sont incohérentes. Le n-ième quartile est la plus petite valeur de la série telle qu'au moins n/4 termes sont inférieurs ou égaux à x, 1-n/4 supérieurs ou égaux à x. Avec la série 1,2,3,4, le premier quartile est 1, le second quartile est 2, le troisième quartile est 3. Le second quartile est distinct de la médiane, qui vaut 2.5 avec la définition donnée dans le document ressource.
Le document ressource précise (page 12) :
Document ressource pour le collège a écrit:
La définition qui est retenue en collège pour la médiane d'une série est celle qui est adoptée dans le programme de seconde.
Si vous avez la curiosité de lire le programme de seconde, vous serez sans doute surpris de constater que, contrairement à ce qu'indique le document ressource pour le collège, le programme cite les médianes et quartiles sans les définir :-) Il n'existe à ma connaissance aucun document d'accompagnement pour le lycée dans lequel une définition des médianes et quartiles est précisée. Ainsi, un professeur de lycée peut définir médianes et quartiles comme bon lui semble, puisque ni le programme, ni les documents d'accompagnement ne précisent cette définition pour le lycée. Naturellement, dans sa grande paresse, le professeur reprendra la définition du manuel (si tant est qu'il y ait une définition dans le manuel...); mais il a toute liberté pour choisir éventuellement la convention du tableur Excell ou de LibreOffice, ou la convention de sa calculatrice préférée. Mieux encore ! Rien ne lui interdit de faire état des différentes conventions, en expliquant les arguments envers l'une ou l'autre, et d'expliquer que, dans le cours, il utilisera telle ou telle convention parce que
o c'est celle du manuel
o c'est celle de LibreOffice
o c'est celle de la TIxx-Stat
(cocher la mention utile).
 ycombeMonarque
ycombeMonarque
En même temps, si tu utilises Excel…Chmick a écrit:ycombe a écrit:Non, ça c'est la définition des programmes, qui n'est pas cohérente. Il y a plusieurs définition des quartiles, GNU R en connait une dizaine.Chmick a écrit:Justement les définitions de médiane et quartiles ne sont pas similaires, en autre le quartile est forcément une valeur de la série contrairement à la médiane dans le cas d'un nombre pair de valeur...
La définition des quartiles dans un manuel de statistique pour le supérieur fait correspondre Q2 avec la médiane, en général.
Oui on est d'accord et c'est justement très embêtant pour la leçon 4ème sans parler du fait que tu ne peux même pas utiliser la fonction quartile d'Excel avec les élèves !
Oui, je sais, la fonction quartile d'openoffice fait pareil.
_________________
Assurbanipal: "Passant, mange, bois, divertis-toi ; tout le reste n’est rien".
Franck Ramus : "Les sciences de l'éducation à la française se font fort de produire un discours savant sur l'éducation, mais ce serait visiblement trop leur demander que de mettre leur discours à l'épreuve des faits".
 ycombeMonarque
ycombeMonarque
Je donne la définition suivante:BR a écrit:Mieux encore ! Rien ne lui interdit de faire état des différentes conventions, en expliquant les arguments envers l'une ou l'autre, et d'expliquer que, dans le cours, il utilisera telle ou telle convention parce que
o c'est celle du manuel
o c'est celle de LibreOffice
o c'est celle de la TIxx-Stat
(cocher la mention utile).
Le n-ième quartile est un nombre telle que n×25% des valeurs lui soient inférieures ou égales et (4-n)×25% lui soient supérieures ou égales.
En pratique, s'il n'y a qu'une valeur possible, c'est une valeur de la série, sinon, les valeurs forment un intervalle compris entre deux valeurs de la série et on prendra le milieu de l'intervalle en question.
Avec ça, Q2 = médiane, MIN et MAX correspondent à Q0 et Q4, comme c'est usuel.
_________________
Assurbanipal: "Passant, mange, bois, divertis-toi ; tout le reste n’est rien".
Franck Ramus : "Les sciences de l'éducation à la française se font fort de produire un discours savant sur l'éducation, mais ce serait visiblement trop leur demander que de mettre leur discours à l'épreuve des faits".
 BRNiveau 9
BRNiveau 9
ycombe a écrit:Je donne la définition suivante:BR a écrit:Mieux encore ! Rien ne lui interdit de faire état des différentes conventions, en expliquant les arguments envers l'une ou l'autre, et d'expliquer que, dans le cours, il utilisera telle ou telle convention parce que
o c'est celle du manuel
o c'est celle de LibreOffice
o c'est celle de la TIxx-Stat
(cocher la mention utile).
Le n-ième quartile est un nombre telle que n×25% des valeurs lui soient inférieures ou égales et (4-n)×25% lui soient supérieures ou égales.
En pratique, s'il n'y a qu'une valeur possible, c'est une valeur de la série, sinon, les valeurs forment un intervalle compris entre deux valeurs de la série et on prendra le milieu de l'intervalle en question.
Avec ça, Q2 = médiane, MIN et MAX correspondent à Q0 et Q4, comme c'est usuel.
Avec cette définition, n'importe quelle valeur inférieure au minimum peut correspondre à Q0 : les valeurs forment un intervalle du type ]-oo,m[ et le milieu de l'intervalle en question est... -oo. De même, Q4 = +oo avec cette convention.
Il me semble qu'une convention usuelle revient à choisir, lorsqu'un intervalle d'extrémités a et b correspond au k-ième quartile, le barycentre de ((a,k);(b,4-k)).
Ainsi, pour Q0, on prend le barycentre de ((-oo,0),(m,4)) c'est à dire la valeur minimale m... Pour Q1, on prend le barycentre de ((a,1),(b,3)) : avec la série de donnée (1,2,3,4), le premier quartile correspond à l'intervalle [1,2[, donc Q1 est le barycentre de ((1,1),(2,3)) c'est à dire 1.75; ce qui est exactement la valeur proposée par LibreOffice Calc...
 bchasaNiveau 9
bchasaNiveau 9
Bonsoir
Voilà ce que j'ai fait cette année avec mes 3èmes pour introduire la notion de médiane.
Tous les élèves ont cherché et ont compris ce qu'était une médiane.
Pour les quartiles j'ai aussi donné une situation problème du même style.
Voilà ce que j'ai fait cette année avec mes 3èmes pour introduire la notion de médiane.
Tous les élèves ont cherché et ont compris ce qu'était une médiane.
Pour les quartiles j'ai aussi donné une situation problème du même style.
 ycombeMonarque
ycombeMonarque
Tu as raison. S'il n'y a qu'une valeur de la série, c'est elle. sinon le milieu de l'intervalle.BR a écrit:ycombe a écrit:Je donne la définition suivante:BR a écrit:Mieux encore ! Rien ne lui interdit de faire état des différentes conventions, en expliquant les arguments envers l'une ou l'autre, et d'expliquer que, dans le cours, il utilisera telle ou telle convention parce que
o c'est celle du manuel
o c'est celle de LibreOffice
o c'est celle de la TIxx-Stat
(cocher la mention utile).
Le n-ième quartile est un nombre telle que n×25% des valeurs lui soient inférieures ou égales et (4-n)×25% lui soient supérieures ou égales.
En pratique, s'il n'y a qu'une valeur possible, c'est une valeur de la série, sinon, les valeurs forment un intervalle compris entre deux valeurs de la série et on prendra le milieu de l'intervalle en question.
Avec ça, Q2 = médiane, MIN et MAX correspondent à Q0 et Q4, comme c'est usuel.
Avec cette définition, n'importe quelle valeur inférieure au minimum peut correspondre à Q0 : les valeurs forment un intervalle du type ]-oo,m[ et le milieu de l'intervalle en question est... -oo. De même, Q4 = +oo avec cette convention.
Il me semble qu'une convention usuelle revient à choisir, lorsqu'un intervalle d'extrémités a et b correspond au k-ième quartile, le barycentre de ((a,k);(b,4-k)).
Ainsi, pour Q0, on prend le barycentre de ((-oo,0),(m,4)) c'est à dire la valeur minimale m... Pour Q1, on prend le barycentre de ((a,1),(b,3)) : avec la série de donnée (1,2,3,4), le premier quartile correspond à l'intervalle [1,2[, donc Q1 est le barycentre de ((1,1),(2,3)) c'est à dire 1.75; ce qui est exactement la valeur proposée par LibreOffice Calc...
Pour les conventions il y en a une dizaines de possibles dans GNU R. Le milieu de l'intervalle si deux valeurs distinctes de la série est le choix fait par mon manuel de proba-stat, par analogie avec la médiane. Cela doit correspondre au type 2 de R.
http://stat.ethz.ch/R-manual/R-patched/library/stats/html/quantile.html
_________________
Assurbanipal: "Passant, mange, bois, divertis-toi ; tout le reste n’est rien".
Franck Ramus : "Les sciences de l'éducation à la française se font fort de produire un discours savant sur l'éducation, mais ce serait visiblement trop leur demander que de mettre leur discours à l'épreuve des faits".
 moi020Niveau 1
moi020Niveau 1
Merci à tous pour vos réponses et le débat intéressant qui a suivi. J'ai cherché quelle activité faire et sans le savoir bchasa j'ai choisi la même que toi !bchasa a écrit:Bonsoir
Voilà ce que j'ai fait cette année avec mes 3èmes pour introduire la notion de médiane.
Tous les élèves ont cherché et ont compris ce qu'était une médiane.
Pour les quartiles j'ai aussi donné une situation problème du même style.
J'espère que cela se passera bien; j'ai testé ma séance aujourd'hui avec mon autre 3ème et ça a été (pourtant ils sont bavards et distraits)
Encore merci à tous pour votre contibution
 User25965Niveau 6
User25965Niveau 6
Je ne suis que remplaçant, et je travaille à l'activité "Casino" suivante, dont tu pourrais peut-être t'inspirer :
Les élèves se voient remettre des dés pipés et non-pipés. Par groupe de 2, ils testent les dés et doivent trouver les dés pipés. Ensuite, la classe forme trois équipes : deux équipes s'affrontent au 421. Une des des équipes utilise les dés pipés, l'autre de vrais dés, mais sous le voile de l'innocence : personne ne sait quelle équipe utilise les dés pipés. Une troisième équipe joue la banque et observe le jeu. A quel moment pourra-t-on découvrir la fraude ?
L'activité mélange probabilités et statistiques. Elle a l'avantage d'être assez proche des domaines connus des jeunes enfants (dés) pour plaire à tous. C'est une bonne activité pour faire un rappel concernant le calcul de P(x) dans le cas d'un événement équiprobable. On peut ensuite introduire la notion de statistique comme étant une série de calculs intervenant après l'événement. Ce qui permet de bien structurer l'analyse de l'élève : avant l'événement, on fait des probas. Après l'événement, on fait des statistiques. Je le précise, car c'est la première idée qui me vient à l'esprit et je ne pense pas avoir lu cela dans des manuels de "daube" comme PHARE. Rappeler que les probabilités et les statistiques sont un des rares domaines des mathématiques qui ont émergé de problèmes concrets (généralement, c'est le contraire : des mathématiques théoriques permettent de résoudre des problèmes concrets, nuances). Bref, les élèves doivent bien percevoir ce que sont les proba et stat par rapport à la géométrie et l'algèbre et bien comprendre en quoi ces domaines sont novateurs en mathématiques.
L'activité n'a pas encore été organisée, sinon je te l'aurais envoyée.
Si tu n'as pas de dés, tu peux produire une série de résultats de tirages, mais c'est moins intéressant.
Bon courage pour ton inspection.
Les élèves se voient remettre des dés pipés et non-pipés. Par groupe de 2, ils testent les dés et doivent trouver les dés pipés. Ensuite, la classe forme trois équipes : deux équipes s'affrontent au 421. Une des des équipes utilise les dés pipés, l'autre de vrais dés, mais sous le voile de l'innocence : personne ne sait quelle équipe utilise les dés pipés. Une troisième équipe joue la banque et observe le jeu. A quel moment pourra-t-on découvrir la fraude ?
L'activité mélange probabilités et statistiques. Elle a l'avantage d'être assez proche des domaines connus des jeunes enfants (dés) pour plaire à tous. C'est une bonne activité pour faire un rappel concernant le calcul de P(x) dans le cas d'un événement équiprobable. On peut ensuite introduire la notion de statistique comme étant une série de calculs intervenant après l'événement. Ce qui permet de bien structurer l'analyse de l'élève : avant l'événement, on fait des probas. Après l'événement, on fait des statistiques. Je le précise, car c'est la première idée qui me vient à l'esprit et je ne pense pas avoir lu cela dans des manuels de "daube" comme PHARE. Rappeler que les probabilités et les statistiques sont un des rares domaines des mathématiques qui ont émergé de problèmes concrets (généralement, c'est le contraire : des mathématiques théoriques permettent de résoudre des problèmes concrets, nuances). Bref, les élèves doivent bien percevoir ce que sont les proba et stat par rapport à la géométrie et l'algèbre et bien comprendre en quoi ces domaines sont novateurs en mathématiques.
L'activité n'a pas encore été organisée, sinon je te l'aurais envoyée.
Si tu n'as pas de dés, tu peux produire une série de résultats de tirages, mais c'est moins intéressant.
Bon courage pour ton inspection.
 marie91270Neoprof expérimenté
marie91270Neoprof expérimenté
Alors cette inspection ?
 wanaxFidèle du forum
wanaxFidèle du forum
C'est sûr, lancer des cubes en plastique pour 'observer', ça forme l'esprit.kellogs a écrit:Je ne suis que remplaçant, et je travaille à l'activité "Casino" suivante, dont tu pourrais peut-être t'inspirer :
Les élèves se voient remettre des dés pipés et non-pipés. Par groupe de 2, ils testent les dés et doivent trouver les dés pipés. Ensuite, la classe forme trois équipes : deux équipes s'affrontent au 421. Une des des équipes utilise les dés pipés, l'autre de vrais dés, mais sous le voile de l'innocence : personne ne sait quelle équipe utilise les dés pipés. Une troisième équipe joue la banque et observe le jeu. A quel moment pourra-t-on découvrir la fraude ?
L'activité mélange probabilités et statistiques. Elle a l'avantage d'être assez proche des domaines connus des jeunes enfants (dés) pour plaire à tous. C'est une bonne activité pour faire un rappel concernant le calcul de P(x) dans le cas d'un événement équiprobable. On peut ensuite introduire la notion de statistique comme étant une série de calculs intervenant après l'événement. Ce qui permet de bien structurer l'analyse de l'élève : avant l'événement, on fait des probas. Après l'événement, on fait des statistiques. Je le précise, car c'est la première idée qui me vient à l'esprit et je ne pense pas avoir lu cela dans des manuels de "daube" comme PHARE. Rappeler que les probabilités et les statistiques sont un des rares domaines des mathématiques qui ont émergé de problèmes concrets (généralement, c'est le contraire : des mathématiques théoriques permettent de résoudre des problèmes concrets, nuances). Bref, les élèves doivent bien percevoir ce que sont les proba et stat par rapport à la géométrie et l'algèbre et bien comprendre en quoi ces domaines sont novateurs en mathématiques.
L'activité n'a pas encore été organisée, sinon je te l'aurais envoyée.
Si tu n'as pas de dés, tu peux produire une série de résultats de tirages, mais c'est moins intéressant.
Bon courage pour ton inspection.
Quant au fait que les probabilités et les statistiques soient l'un des rares domaines des mathématiques qui aient émergé de problèmes concrets, c'est tout simplement faux.
 User25965Niveau 6
User25965Niveau 6
C'est juste wanax, j'y suis allé un peu fort.
Page 1 sur 2 • 1, 2 

Permission de ce forum:
Vous ne pouvez pas répondre aux sujets dans ce forum



