Page 3 sur 4 •  1, 2, 3, 4
1, 2, 3, 4 
 1, 2, 3, 4
1, 2, 3, 4 
- CeladonDemi-dieu
En effet. Mais keskimarive ? 10 = 1 + 2 + 1 + 2+ 1 !!!JPhMM a écrit:Même pas. :lol:Celadon a écrit:Tu utilises les légos et un petit bonhomme sur 10 marches, il compte les pas et tu reproduis la scène 42 fois... Bonne soirée !
Car : 10 = 1 + 2 + 1 + 2 + 1
2 fois, cela donnerait : 10 + 10 = 1 + 2 + 1 + 2 + 1 + 1 + 2 + 1 + 2 + 1
Avec 6, oui ça marche.
6 = 1 + 2 + 1 + 2 = deux 1 et deux 2.
6 x 70 = (deux 1 et deux 2) x 70 = cent quarante 1 et cent quarante 2.

 MirobolandeHabitué du forum
MirobolandeHabitué du forum
En tout cas, ce n'est pas un problème que je donnerais en devoirs en CE1...
 doublecasquetteEnchanteur
doublecasquetteEnchanteur
JPhMM a écrit:Non.Nita a écrit:3) la personne qui a donné la première une réponse exacte... est prof de lettres.
La première réponse exacte est:Patissot a écrit: Avec deux pas je monte trois marches, donc avec 140x2 pas je monte...
Ah mais oui mais non... Nous avons tous donné la réponse en même temps sauf que, quand nous avons essayé d'envoyer notre message, l'ordre d'arrivée a peut-être bien été perturbé par la longueur des propos.
Tiens, ça ferait un chouette problème de CE1 ou de CP, ça ! Sachant le nombre de lettres et signes de chacun des messages, sans tenir compte de la vitesse de frappe qu'on fixera à 1 seconde pour le 1er signe et 2 secondes pour le 2e signe et ainsi de suite, calculez à quelle heure exacte chacun des contributeurs a commencé à rédiger le sien...
Pour ceux qui comme moi pensent que le problème du phare n'est pas un problème de CE1, il faut aller voir dans le fichier ERMEL de la même classe.
Je me souviens qu'à la fin, il y a un problème sur les points d'un match de rugby où il faut chercher combien les deux équipes ont pu marquer d'essais et combien en ont-ils transformé pour obtenir chacune le score final ( :| je vais encore me faire jeter parce que ces nullardes de PE ne connaissent rien au rugby et que ce n'est pas ça qu'on dit...).
Dans le livre du maître, on nous explique qu'il faut déstabiliser les élèves en leur proposant dès le début des travaux où il n'y a pas qu'une seule solution ainsi que des travaux qu'ils doivent résoudre par tâtonnement complet sans disposer d'aucune des procédures expertes utilisées habituellement par l'adulte mathématisé.
 CeladonDemi-dieu
CeladonDemi-dieu
On voit le résultat ! De plus en plus de carrières scientifiques en perspective, du calcul mental qui, même pratiqué tous les matins, ne réveille pas les neurones, en effet, ils sont bien déstabilisés les élèves ERMEL.
 JPhMMDemi-dieu
JPhMMDemi-dieu
Bien vu ! j'ai oublié un +(1+2)Celadon a écrit:En effet. Mais keskimarive ? 10 = 1 + 2 + 1 + 2+ 1 !!!JPhMM a écrit:Même pas. :lol:Celadon a écrit:Tu utilises les légos et un petit bonhomme sur 10 marches, il compte les pas et tu reproduis la scène 42 fois... Bonne soirée !
Car : 10 = 1 + 2 + 1 + 2 + 1
2 fois, cela donnerait : 10 + 10 = 1 + 2 + 1 + 2 + 1 + 1 + 2 + 1 + 2 + 1
Avec 6, oui ça marche.
6 = 1 + 2 + 1 + 2 = deux 1 et deux 2.
6 x 70 = (deux 1 et deux 2) x 70 = cent quarante 1 et cent quarante 2.


C'est corrigé, merci.
_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
 Winnie88500Niveau 5
Winnie88500Niveau 5
Un peu trop facile ce problème ! J'espère que les gamins de CE1 auront droit aux variantes lundi.
Variante 1 : on ajoute qu'Alex descend 3 marches toutes les 10 marches.
Variante 2 : on ajoute qu'Alex saute à pieds joints toutes les 50 marches.
Variante 3 : Alex a le choix : à chaque pas, il peut monter une marche ou deux marches. Combien y-a-t-il de façons de monter l'escalier ?
Variante 4 : quel est l'âge du gardien de phare ?
Variante 5 : expliquer pourquoi Alex s'est cassé la gueule dans les escaliers.
Variante 1 : on ajoute qu'Alex descend 3 marches toutes les 10 marches.
Variante 2 : on ajoute qu'Alex saute à pieds joints toutes les 50 marches.
Variante 3 : Alex a le choix : à chaque pas, il peut monter une marche ou deux marches. Combien y-a-t-il de façons de monter l'escalier ?
Variante 4 : quel est l'âge du gardien de phare ?
Variante 5 : expliquer pourquoi Alex s'est cassé la gueule dans les escaliers.
 KakHabitué du forum
KakHabitué du forum
réponse de ma puce (CE1):
420:2
210 pas où il fait une marche
210:2 car il fait deux marches ensemble
=105
315 pas en tout

édit: "je ne suis pas une puce , je suis ta fille!"
édit: pourquoi ça ne marche pas le raisonnement dema puce ma fille?
420:2
210 pas où il fait une marche
210:2 car il fait deux marches ensemble
=105
315 pas en tout

édit: "je ne suis pas une puce , je suis ta fille!"
édit: pourquoi ça ne marche pas le raisonnement de
 VudiciFidèle du forum
VudiciFidèle du forum
:lol!:Winnie88500 a écrit:Un peu trop facile ce problème ! J'espère que les gamins de CE1 auront droit aux variantes lundi.
Variante 1 : on ajoute qu'Alex descend 3 marches toutes les 10 marches.
Variante 2 : on ajoute qu'Alex saute à pieds joints toutes les 50 marches.
Variante 3 : Alex a le choix : à chaque pas, il peut monter une marche ou deux marches. Combien y-a-t-il de façons de monter l'escalier ?
Variante 4 : quel est l'âge du gardien de phare ?
Variante 5 : expliquer pourquoi Alex s'est cassé la gueule dans les escaliers.
_________________
Front de Libération des Lichens Injustement Massacrés
 VudiciFidèle du forum
VudiciFidèle du forum
Le gamin aurait pu tenter une réponse du genre...


_________________
Front de Libération des Lichens Injustement Massacrés
 KakHabitué du forum
KakHabitué du forum
Vudici a écrit:Le gamin aurait pu tenter une réponse du genre...
Elle est juste cette réponse!
 JPhMMDemi-dieu
JPhMMDemi-dieu
L'erreur est très subtile. En divisant 420 par 2, taKak a écrit:réponse de ma puce (CE1):
420:2
210 pas où il fait une marche
210:2 car il fait deux marches ensemble
=105
315 pas en tout

édit: "je ne suis pas une puce , je suis ta fille!"
Quand on fait un pas d'une marche puis un pas de deux marches, on fait au total 3 marches.
Donc il faut faire 420:3=140
140 pas pour faire 140 marches.
140 pas pour faire 140+140 marches.
Total 280 pas.
_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
 KakHabitué du forum
KakHabitué du forum
JPhMM a écrit:L'erreur est très subtile. En divisant 420 par 2, taKak a écrit:réponse de ma puce (CE1):
420:2
210 pas où il fait une marche
210:2 car il fait deux marches ensemble
=105
315 pas en tout

édit: "je ne suis pas une puce , je suis ta fille!"pucefille suppose qu'au total on fait autant de marches quand on fait une marche en un pas que quand on fait deux marches en un pas. Or c'est faux.
Quand on fait un pas d'une marche puis un pas de deux marches, on fait au total 3 marches.
Donc il faut faire 420:3=140
140 pas pour faire 140 marches.
140 pas pour faire 140+140 marches.
Total 280 pas.
Je comprends bien ton raisonnement (je fais le même ainsi que les adultes autour d'elle) ... Ma fille n'a pas réfléchi très longtemps mais moi je suis perplexe... L'erreur est trop subtile pour moi

conclusion: ce problème est fait pour les adultes!
 JPhMMDemi-dieu
JPhMMDemi-dieu
Si tu veux, on peut essayer de décortiquer le raisonnement.
Ta fille applique aux marches le raisonnement qu'il faut appliquer aux pas (ce qui est tout à fait normal si on n'a aucune notion des équations, ou des programmes de calcul).
Je résume.
Supposons qu'on connaisse le nombre de pas. Disons 100 pas.
100:2 = 50 pas.
50 pas permettent de faire 50 marches.
Et 50 autres pas permettent de faire 2x50=100 marches.
On aurait donc fait 150 marches=3x50 marches.
(Remarque : un élève de l’Égypte antique ou de Mésopotamie pourrait résoudre le problème ainsi, par l'algorithme de la fausse position. Actuellement (sauf les ordinateurs) personne ne fait ainsi. On utilise les équations, ou — mentalement — les programmes de calcul (ce qui est presque la même chose)).
Programme de calcul correspondant :
On choisit un nombre de pas => On le divise par 2. => On multiplie le résultat pas 3 => Le résultat est le nombre de marches.
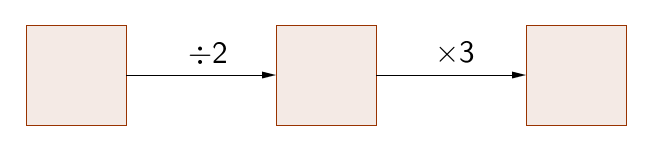
Si le nombre de marches est 420, il faut faire le programme de calcul dans le sens inverse (donc prendre les opérations inverses, certes, mais aussi les appliquer en sens inverse. Voyons cela).
Or quel nombre multiplié par 3 fait 420 ? C'est 420 : 3 = 140.
Et quel nombre divisé par 2 fait 140 ? C'est 2 x 140 = 280.
On a donc trouvé le nombre de pas qui, appliqué au calcul, donne 420.
Ta fille applique aux marches le raisonnement qu'il faut appliquer aux pas (ce qui est tout à fait normal si on n'a aucune notion des équations, ou des programmes de calcul).
Je résume.
Supposons qu'on connaisse le nombre de pas. Disons 100 pas.
100:2 = 50 pas.
50 pas permettent de faire 50 marches.
Et 50 autres pas permettent de faire 2x50=100 marches.
On aurait donc fait 150 marches=3x50 marches.
(Remarque : un élève de l’Égypte antique ou de Mésopotamie pourrait résoudre le problème ainsi, par l'algorithme de la fausse position. Actuellement (sauf les ordinateurs) personne ne fait ainsi. On utilise les équations, ou — mentalement — les programmes de calcul (ce qui est presque la même chose)).
Programme de calcul correspondant :
On choisit un nombre de pas => On le divise par 2. => On multiplie le résultat pas 3 => Le résultat est le nombre de marches.

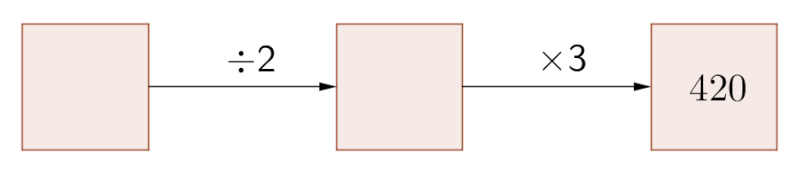
Si le nombre de marches est 420, il faut faire le programme de calcul dans le sens inverse (donc prendre les opérations inverses, certes, mais aussi les appliquer en sens inverse. Voyons cela).

Or quel nombre multiplié par 3 fait 420 ? C'est 420 : 3 = 140.
Et quel nombre divisé par 2 fait 140 ? C'est 2 x 140 = 280.
On a donc trouvé le nombre de pas qui, appliqué au calcul, donne 420.
_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
 frimoussette77Guide spirituel
frimoussette77Guide spirituel
La réponse donnée me plaît bienKak a écrit:Vudici a écrit:Le gamin aurait pu tenter une réponse du genre...
Elle est juste cette réponse!
La formule est bizarre au bout de 5 ans il n'y a plus de cerfs ?
 DalvaVénérable
DalvaVénérable
Avec tout ça, on passe à côté de l'essentiel.
La formule exacte, c'est "enduire d'horreur". Faut réviser ses classiques !
(Moi aussi, je suis étonnée du problème donné en CE1.)
La formule exacte, c'est "enduire d'horreur". Faut réviser ses classiques !
(Moi aussi, je suis étonnée du problème donné en CE1.)
 User5899Demi-dieu
User5899Demi-dieu
Voui. Mais il a été présupposé que ces dix étages sont égaux...Gryphe a écrit:Le coup des 10 étages, je trouve ça bien !oceanovox a écrit:Bon, au final, j'ai trouvé comment procéder.
J'ai dessiné un phare que j'ai divisé en 10 étages (pour lui faire comprendre comment et pourquoi on passe de 420 à 42).
 User5899Demi-dieu
User5899Demi-dieu
Le gamin est pertinent, mais la pauvre biche qui va mettre bas 80 cerfs...Vudici a écrit:Le gamin aurait pu tenter une réponse du genre...

 YazilikayaNeoprof expérimenté
YazilikayaNeoprof expérimenté
oceanovox a écrit:Il est en CE1.
Voici l'énoncé :
Alex monte au sommet du phare de 420 marches d'une drôle de façon.
Avec le 1er pas, il monte une marche, avec le 2ème pas, il monte deux marches, avec le 3ème pas, il monte une marche, avec le 4ème pas, il monte deux marches... et ainsi de suite.
Combien doit-il faire de pas pour arriver en haut du phare?
Comment me conseillez-vous de procéder avec lui?
merci d'avance
Toi, tu fréquentes auf. J'avais répondu que pour des CE1, la vache.
 miss sophieExpert spécialisé
miss sophieExpert spécialisé
Cripure a écrit:Le gamin est pertinent, mais la pauvre biche qui va mettre bas 80 cerfs...Vudici a écrit:Le gamin aurait pu tenter une réponse du genre...
J'adore la réponse de l'élève... et votre commentaire !
 GrypheMédiateur
GrypheMédiateur
C'est vrai qu'on pourrait corser le problème...Cripure a écrit:Mais il a été présupposé que ces dix étages sont égaux...
Quelle idée de poser une question pareille à des CE1, franchement.
_________________
Τί ἐστιν ἀλήθεια ;
 roxanneOracle
roxanneOracle
 nova32Niveau 9
nova32Niveau 9
Il me semble, vu l'énoncé et le nom du personnage (Alex) que ce problème vient de Cap Maths. Mais je peux me tromper, j'ai le bouquin à l'école, je ne peux pas vérifier.
 doublecasquetteEnchanteur
doublecasquetteEnchanteur
nova32 a écrit:Il me semble, vu l'énoncé et le nom du personnage (Alex) que ce problème vient de Cap Maths. Mais je peux me tromper, j'ai le bouquin à l'école, je ne peux pas vérifier.
Je m'en doutais ! Le petit frère d'Ermel fait dans les phares et balises alors que l'aîné visait les rugbymen ! Quand est-ce que les adultes arrêteront d'essayer de se projeter dans des cerveaux d'enfants pour leur faire passer une soupe même pas adaptée à leur âge ?
Ils ne peuvent pas relire Boucle d'Or et les Trois Ours avant de concevoir des problèmes de maths à la gomme ?



Tiens, en échange un problème de CM2 (début d'année) de 1960 (j'ai transformé le paysan en marcheur, les paysans vont de champ en champ en quad, actuellement).
14. Un marcheur fait 120 pas à la minute. Son pas mesure 75 cm.
a) Quelle distance, en cm, puis en m, ce marcheur parcourt-il en 1 minute ?
b) Ce marcheur a mis 6 minutes pour faire le tour d’un terrain carré. Quel est le périmètre de ce terrain ? quel est son côté ?
 nova32Niveau 9
nova32Niveau 9
Oui, je suis quasiment certain, je visualise bien la page avec le phare.
Les problèmes de Cap Maths sont affreux, tout autant que la méthode dans son ensemble. J'ai testé un an, je ne recommencerai plus !
Les problèmes de Cap Maths sont affreux, tout autant que la méthode dans son ensemble. J'ai testé un an, je ne recommencerai plus !
 AmaliahEmpereur
AmaliahEmpereur
roxanne a écrit:Bah, ça occupe les parents ...Mais je ne suis pas pressée d'y être...(sinon, c'est pas interdit les devoirs écrits en primaire ?)
Rien à voir avec le sujet initial, mais franchement je trouve ça pire, les leçons à apprendre! Je préfère cent fois faire faire des exercices que faire apprendre une leçon à mon fils. Au moins il est plus actif, la leçon, il se tortille sur sa chaise, se dandine, n'a aucune envie de l'apprendre, tout bon élève qu'il est... Au moins, un exercice, il a le stylo en main et il le fait! C'est plus concret et moins dur à gérer, je trouve.
Page 3 sur 4 •  1, 2, 3, 4
1, 2, 3, 4 
 1, 2, 3, 4
1, 2, 3, 4 
Permission de ce forum:
Vous ne pouvez pas répondre aux sujets dans ce forum


