Page 1 sur 2 • 1, 2 

 LotacheNiveau 2
LotacheNiveau 2
Bonjour les profs de math et autres fans de problèmes !
Je reposte ici parce que la dernière fois vous m'avez tous été d'une grande aide.
Voici mon problème: j'ai 10 équipes (A, B, C,...J) qui doivent toutes rencontrer chaque équipe adverse 1 fois. Ca nous fait 45 rencontres, 9x5 rencontres qui ont lieu en simultané sur 9 créneaux (1, 2, 3,... 9).
Ces rencontres peuvent s'organiser de la façon suivante:
1 -> AH, BC, DG, EF, JI
2 -> CA, FJ, GE, DH, IB
3 -> AI, BF, CD, HG, JE
4 -> CH, BE, FA, GJ, ID
5 -> AE, BJ, CG, DF, HI
6 -> ED, FH, GB, IC, JA
7 -> AB, CF, DJ, HE, IG
8 -> AG, B, EC, FI, JH
9 -> CJ, DA, GF, HB, IE
Sachant qu'il y a 9 stands, que chaque équipe doit passer une fois sur chaque stand et que chaque stand n'est disponible qu'une fois par créneau, comment répartir les rencontres?
J'ai essayé la méthode "au hasard" ça bloque très vite, évidemment, et je ne sais pas comment prendre le problème pour gérer la répartition.
Merci à tous ceux qui essaieront !
Lotache.
Je reposte ici parce que la dernière fois vous m'avez tous été d'une grande aide.
Voici mon problème: j'ai 10 équipes (A, B, C,...J) qui doivent toutes rencontrer chaque équipe adverse 1 fois. Ca nous fait 45 rencontres, 9x5 rencontres qui ont lieu en simultané sur 9 créneaux (1, 2, 3,... 9).
Ces rencontres peuvent s'organiser de la façon suivante:
1 -> AH, BC, DG, EF, JI
2 -> CA, FJ, GE, DH, IB
3 -> AI, BF, CD, HG, JE
4 -> CH, BE, FA, GJ, ID
5 -> AE, BJ, CG, DF, HI
6 -> ED, FH, GB, IC, JA
7 -> AB, CF, DJ, HE, IG
8 -> AG, B, EC, FI, JH
9 -> CJ, DA, GF, HB, IE
Sachant qu'il y a 9 stands, que chaque équipe doit passer une fois sur chaque stand et que chaque stand n'est disponible qu'une fois par créneau, comment répartir les rencontres?
J'ai essayé la méthode "au hasard" ça bloque très vite, évidemment, et je ne sais pas comment prendre le problème pour gérer la répartition.
Merci à tous ceux qui essaieront !
Lotache.
 EnaecoVénérable
EnaecoVénérable
Les rencontres que tu as indiquées sont-elles fixes ?
Peut-on changer les confrontations à l'intérieur d'un stand, tant qu'on respecte le critère "tout le monde rencontre tout le monde" ?
Peut-on changer les confrontations à l'intérieur d'un stand, tant qu'on respecte le critère "tout le monde rencontre tout le monde" ?
 EolullNiveau 3
EolullNiveau 3
Bonjour,
là comme ça à chaud je ne vois pas vraiment de méthode astucieuse pour générer des solutions. A la main ça n'a pas l'air simple (bon après je n'ai cherché que 10 minutes).
En revanche je suis confiant qu'un programme récursif type backtracking (comme ceux qu'on utilise pour résoudre des Sudoku) trouverait une (ou des) solutions assez facilement, si cela existe, ça s'y prête bien normalement. A strictement parler ce n'est pas vraiment des maths mais de l'algorithmique, mais bon, ça résoudrait le problème.
Quand j'aurais un moment je proposerais un programme et une solution, ça a l'air amusant...
Bonne soirée
là comme ça à chaud je ne vois pas vraiment de méthode astucieuse pour générer des solutions. A la main ça n'a pas l'air simple (bon après je n'ai cherché que 10 minutes).
En revanche je suis confiant qu'un programme récursif type backtracking (comme ceux qu'on utilise pour résoudre des Sudoku) trouverait une (ou des) solutions assez facilement, si cela existe, ça s'y prête bien normalement. A strictement parler ce n'est pas vraiment des maths mais de l'algorithmique, mais bon, ça résoudrait le problème.
Quand j'aurais un moment je proposerais un programme et une solution, ça a l'air amusant...
Bonne soirée
 angelxxxÉrudit
angelxxxÉrudit
Bon, je ne suis pas prof de math, mais je pense que j'ai trouvé une méthode qui fonctionne :
Tu traces un cercle avec 10 crans, tu les numérotes : A, B ...
Tu en fais un deuxième plus petit, et pareil sauf que tu décales tout d'un cran
Il te reste à tourner un des deux cercles d'un tour à chaque fois et tu auras toutes les combinaisons possibles.
Ca ressemble un peu au jeu dooble, en beaucoup plus facile
C'est possible de résoudre avec un simple tableau double entrée aussi, mais c'était trop long à rédiger :p
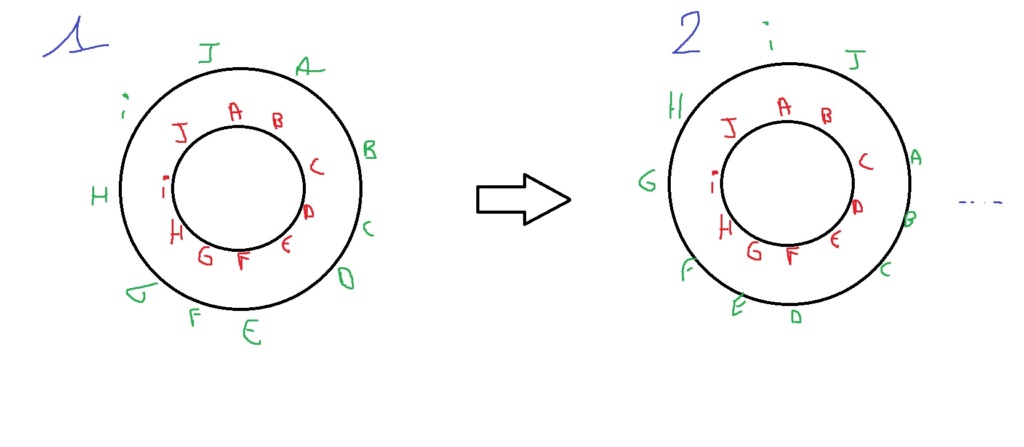
Tu traces un cercle avec 10 crans, tu les numérotes : A, B ...
Tu en fais un deuxième plus petit, et pareil sauf que tu décales tout d'un cran
Il te reste à tourner un des deux cercles d'un tour à chaque fois et tu auras toutes les combinaisons possibles.
Ca ressemble un peu au jeu dooble, en beaucoup plus facile

C'est possible de résoudre avec un simple tableau double entrée aussi, mais c'était trop long à rédiger :p

_________________
"La lumière pense voyager plus vite que quoi que ce soit d'autre, mais c'est faux. Peu importe à quelle vitesse voyage la lumière, l'obscurité arrive toujours la première, et elle l'attend. Terry Pratchett."
 LotacheNiveau 2
LotacheNiveau 2
Merci pour vos réponses !
angelxxx --> Alors ta solution, c'est plus pour créer une rotation pour les rencontres que pour les répartir sur les stands non? Si c'est le cas, j'ai déjà une répartition des équipes possible (voir premier post) et en plus, malheureusement, ta solution ne fonctionne pas puisque je me retrouverais avec l'équipe A qui joue en même temps contre la J et la B, la G qui rencontre à la fois la H et la F, etc.
Et si on utilise ta technique pour répartir les rencontres sur les stands, on se retrouve avec un cercle à 45 entrées et un cercle à 9 entrée... Pas terrible non plus.
Merci d'avoir essayé en tous cas. C'est plus difficile que ça n'en a l'air
Kanpindon --> C'est exactement ce à quoi j'ai l'impression de faire face, un Sudoku, mais je ne sais pas comment le coucher sur le papier. Déjà pour la mise en place des rencontres, c'était coton, c'est un collègue qui m'a trouvé la solution sur un site de création de championnat de foot hehe
angelxxx --> Alors ta solution, c'est plus pour créer une rotation pour les rencontres que pour les répartir sur les stands non? Si c'est le cas, j'ai déjà une répartition des équipes possible (voir premier post) et en plus, malheureusement, ta solution ne fonctionne pas puisque je me retrouverais avec l'équipe A qui joue en même temps contre la J et la B, la G qui rencontre à la fois la H et la F, etc.
Et si on utilise ta technique pour répartir les rencontres sur les stands, on se retrouve avec un cercle à 45 entrées et un cercle à 9 entrée... Pas terrible non plus.
Merci d'avoir essayé en tous cas. C'est plus difficile que ça n'en a l'air

Kanpindon --> C'est exactement ce à quoi j'ai l'impression de faire face, un Sudoku, mais je ne sais pas comment le coucher sur le papier. Déjà pour la mise en place des rencontres, c'était coton, c'est un collègue qui m'a trouvé la solution sur un site de création de championnat de foot hehe
 TungstèneNiveau 5
TungstèneNiveau 5
angelxxx a écrit:Tu traces un cercle avec 10 crans, tu les numérotes : A, B ...
Tu en fais un deuxième plus petit, et pareil sauf que tu décales tout d'un cran [...]
J'ai peur, si j'ai bien compris ta proposition, qu'elle ne fonctionne pas en l'état car B (par exemple) ne peut pas rencontrer A et C dans le même créneau (ta double-roue numérotée 1 semble proposer cette situation).
 SeismiMineNiveau 5
SeismiMineNiveau 5
Il me semble que vouloir faire un tableau de 9x5 affrontements où chaque ligne contient tout le monde et où chaque personne va dans chaque colonne au moins une fois n'est pas possible en général (seulement dans des cas particuliers).
Une grande raison pour moi serait que 9 ne divise pas 10.
Un cas plus simple avec 4 participants (donc 6 rencontres au total, 3 rounds de 2 rencontres) est impossible par exemple.
Au moins l'un des participants restera toujours dans la même colonne.
AB CD (ligne obligatoire)
BD AC (on met A en 2e colonne, qui affronte C ou D)
AD BC (on met B en 2e colonne, on remplit)
Ici c'est C qui ne change pas de colonne.
Une grande raison pour moi serait que 9 ne divise pas 10.
Un cas plus simple avec 4 participants (donc 6 rencontres au total, 3 rounds de 2 rencontres) est impossible par exemple.
Au moins l'un des participants restera toujours dans la même colonne.
AB CD (ligne obligatoire)
BD AC (on met A en 2e colonne, qui affronte C ou D)
AD BC (on met B en 2e colonne, on remplit)
Ici c'est C qui ne change pas de colonne.
 LotacheNiveau 2
LotacheNiveau 2
Bonsoir SeismiMine -> A mince... Donc en fait c'est tout bonnement impossible?
 Mrs HobieGrand sage
Mrs HobieGrand sage
pas le temps d'y réfléchir, mais en modélisant avec un graphe ?
_________________

 Plus tu pédales moins vite, moins t'avances plus vite.
Plus tu pédales moins vite, moins t'avances plus vite.Et même que la marmotte, elle met les stylos-plumes dans les jolis rouleaux

Tutylatyrée Ewok aux Doigts Agiles, Celle qui Abrite les Plumes aux Écrits Sagaces, Rapide Chevalier sur son Coursier Mécanique
 PrezboGrand Maître
PrezboGrand Maître
Lotache a écrit:Bonjour les profs de math et autres fans de problèmes !
Je reposte ici parce que la dernière fois vous m'avez tous été d'une grande aide.
Voici mon problème: j'ai 10 équipes (A, B, C,...J) qui doivent toutes rencontrer chaque équipe adverse 1 fois. Ca nous fait 45 rencontres, 9x5 rencontres qui ont lieu en simultané sur 9 créneaux (1, 2, 3,... 9).
Ces rencontres peuvent s'organiser de la façon suivante:
1 -> AH, BC, DG, EF, JI
2 -> CA, FJ, GE, DH, IB
3 -> AI, BF, CD, HG, JE
4 -> CH, BE, FA, GJ, ID
5 -> AE, BJ, CG, DF, HI
6 -> ED, FH, GB, IC, JA
7 -> AB, CF, DJ, HE, IG
8 -> AG, B, EC, FI, JH
9 -> CJ, DA, GF, HB, IE
Sachant qu'il y a 9 stands, que chaque équipe doit passer une fois sur chaque stand et que chaque stand n'est disponible qu'une fois par créneau, comment répartir les rencontres?
Bonjour,
je n'ai pas le temps d'y réfléchir dans l’immédiat mais je ne suis pas sûr de comprendre cette histoire de stands. Tu veux dire que les rencontres ont lieu sur des stands, qu'il existe neuf stand, qu'à chaque créneau 5 des 9 stands sont occupés et qu'au bout des 9 créneaux chaque équipe doit être passé sur chaque stand une fois et une seule ?
 mathmaxExpert spécialisé
mathmaxExpert spécialisé
Tu es sûr que c’est possible ? Parceque si on prend 4 équipes et 3 stands, c’est impossible que chaque équipe passe sur chaque stand une fois.
_________________
« Les machines un jour pourront résoudre tous les problèmes, mais jamais aucune d'entre elles ne pourra en poser un ! »
Albert Einstein
 MathadorEmpereur
MathadorEmpereur
Je ne suis pas sûr, en effet, que cela soit possible.
En tout cas on peut se ramener à un problème classique: on attribue à chaque rencontre AB, AC, etc. un sommet et on relie deux sommets entre eux s'ils ont une équipe en commun.
Ce que tu cherches correspond alors à un 5-coloriage du graphe.
Edit: tu imposes aussi 9 sommets par couleur, on s'écarte donc d'un véritable coloriage de graphe.
Edit2: je crois qu'il y a quelque chose de pas clair. Cherches-tu à faire 9 rencontres en même temps 5 fois, 5 rencontres 9 fois ou autre chose ?
En tout cas on peut se ramener à un problème classique: on attribue à chaque rencontre AB, AC, etc. un sommet et on relie deux sommets entre eux s'ils ont une équipe en commun.
Ce que tu cherches correspond alors à un 5-coloriage du graphe.
Edit: tu imposes aussi 9 sommets par couleur, on s'écarte donc d'un véritable coloriage de graphe.
Edit2: je crois qu'il y a quelque chose de pas clair. Cherches-tu à faire 9 rencontres en même temps 5 fois, 5 rencontres 9 fois ou autre chose ?
_________________
"There are three kinds of lies: lies, damned lies, and statistics." (cité par Mark Twain)
« Vulnerasti cor meum, soror mea, sponsa; vulnerasti cor meum in uno oculorum tuorum, et in uno crine colli tui.
Quam pulchrae sunt mammae tuae, soror mea sponsa! pulchriora sunt ubera tua vino, et odor unguentorum tuorum super omnia aromata. » (Canticum Canticorum 4:9-10)
 mathmaxExpert spécialisé
mathmaxExpert spécialisé
Je crois que ce n’est pas possible : A rencontre B sur un stand, et C sur un autre, mettons le 1 et le 2. Lorsque B rencontre C ils ne peuvent utiliser ni le 1 ni le 2. Il ne leur reste donc que 7 stands. Pour BD, il restera 6 stands, pour BE 5,... il n’y a plus de stand possible pour BJ.
_________________
« Les machines un jour pourront résoudre tous les problèmes, mais jamais aucune d'entre elles ne pourra en poser un ! »
Albert Einstein
 angelxxxÉrudit
angelxxxÉrudit
Ok, je suis fatigué, je n'avais pas tout compris, désolé !
Autre proposition.. Mais mon cerveau n'est toujours pas à fond ! Sinon, il faudra attendre demain.
Édit : c'est évidemment faux.. je laisse au cas où ça donne une idée à d'autres !
Pour le dooble une très bonne vidéo : https://www.youtube.com/watch?v=VTDKqW_GLkw
Autre proposition.. Mais mon cerveau n'est toujours pas à fond ! Sinon, il faudra attendre demain.
Édit : c'est évidemment faux.. je laisse au cas où ça donne une idée à d'autres !

Pour le dooble une très bonne vidéo : https://www.youtube.com/watch?v=VTDKqW_GLkw
_________________
"La lumière pense voyager plus vite que quoi que ce soit d'autre, mais c'est faux. Peu importe à quelle vitesse voyage la lumière, l'obscurité arrive toujours la première, et elle l'attend. Terry Pratchett."
 angelxxxÉrudit
angelxxxÉrudit
mathmax a écrit:Je crois que ce n’est pas possible : A rencontre B sur un stand, et C sur un autre, mettons le 1 et le 2. Lorsque B rencontre C ils ne peuvent utiliser ni le 1 ni le 2. Il ne leur reste donc que 7 stands. Pour BD, il restera 6 stands, pour BE 5,... il n’y a plus de stand possible pour BJ.
Hum, non ?
Tu exclus une possibilité pour B, et une pour C; mais effectivement 2 différentes pour BC, ce qui ne pose pas forcément problème.
_________________
"La lumière pense voyager plus vite que quoi que ce soit d'autre, mais c'est faux. Peu importe à quelle vitesse voyage la lumière, l'obscurité arrive toujours la première, et elle l'attend. Terry Pratchett."
 SeismiMineNiveau 5
SeismiMineNiveau 5
Prezbo a écrit:Lotache a écrit:Bonjour les profs de math et autres fans de problèmes !
Je reposte ici parce que la dernière fois vous m'avez tous été d'une grande aide.
Voici mon problème: j'ai 10 équipes (A, B, C,...J) qui doivent toutes rencontrer chaque équipe adverse 1 fois. Ca nous fait 45 rencontres, 9x5 rencontres qui ont lieu en simultané sur 9 créneaux (1, 2, 3,... 9).
Ces rencontres peuvent s'organiser de la façon suivante:
1 -> AH, BC, DG, EF, JI
2 -> CA, FJ, GE, DH, IB
3 -> AI, BF, CD, HG, JE
4 -> CH, BE, FA, GJ, ID
5 -> AE, BJ, CG, DF, HI
6 -> ED, FH, GB, IC, JA
7 -> AB, CF, DJ, HE, IG
8 -> AG, B, EC, FI, JH
9 -> CJ, DA, GF, HB, IE
Sachant qu'il y a 9 stands, que chaque équipe doit passer une fois sur chaque stand et que chaque stand n'est disponible qu'une fois par créneau, comment répartir les rencontres?
Bonjour,
je n'ai pas le temps d'y réfléchir dans l’immédiat mais je ne suis pas sûr de comprendre cette histoire de stands. Tu veux dire que les rencontres ont lieu sur des stands, qu'il existe neuf stand, qu'à chaque créneau 5 des 9 stands sont occupés et qu'au bout des 9 créneaux chaque équipe doit être passé sur chaque stand une fois et une seule ?
Une et une seule fois cela est impossible car 45 n'est pas un multiple de 10.
Et le "au moins une fois" (certaines équipes passant plusieurs fois sur le même) ne semble pas marcher non plus (impossible pour n=4, alors pour n=10 j'en doute).
Pour n impair cela devrait fonctionner, parce que le nombre de passages (n.(n-1)/2) est alors un multiple de n. En particulier on a autant de lignes que de participants.
Un exemple avec n=5 (chaque tour une équipe ne combat pas) qui fonctionne.
AB CD E
EC BD A
AC ED B
AD EB C
BC AE D
Avec 9 équipes (36 passages) je pense que tu auras facilement une répartition fonctionnelle.
 mathmaxExpert spécialisé
mathmaxExpert spécialisé
Ce que propose Angelxx marche pour l’attribution des stands, mais risque de bloquer pour les créneaux (chaque stand n’est disponible que pour un match à chaque étape, et chaque équipe joue un seul match par étape). Pour 4 équipes avec le même tableau on obtient
AB stand 1, AC stand 2, AD stand 3, BC stand 3, BD stand 2 CD stand 1. Chaque équipe semble bien passer une fois dans chaque stand. Mais quand on veut organiser les tours ça bloque. Il faut faire AB et CD au même tour, or tous deux sont dans le stand 1. Même en changeant la répartition des stands ça bloque :
AB et CD
AC et BD,
AD et BC.
Si A parcourt bien les trois stands, au deuxième tour soit B soit D auront le même stand qu’au premier.8
Pour 10 équipes je ne vois pas où mais je pense que cela bloque aussi.
SeisMimine est-ce que tu peux attribuer les stands avec ta solution ?
AB stand 1, AC stand 2, AD stand 3, BC stand 3, BD stand 2 CD stand 1. Chaque équipe semble bien passer une fois dans chaque stand. Mais quand on veut organiser les tours ça bloque. Il faut faire AB et CD au même tour, or tous deux sont dans le stand 1. Même en changeant la répartition des stands ça bloque :
AB et CD
AC et BD,
AD et BC.
Si A parcourt bien les trois stands, au deuxième tour soit B soit D auront le même stand qu’au premier.8
Pour 10 équipes je ne vois pas où mais je pense que cela bloque aussi.
SeisMimine est-ce que tu peux attribuer les stands avec ta solution ?
_________________
« Les machines un jour pourront résoudre tous les problèmes, mais jamais aucune d'entre elles ne pourra en poser un ! »
Albert Einstein
 mathmaxExpert spécialisé
mathmaxExpert spécialisé
angelxxx a écrit:mathmax a écrit:Je crois que ce n’est pas possible : A rencontre B sur un stand, et C sur un autre, mettons le 1 et le 2. Lorsque B rencontre C ils ne peuvent utiliser ni le 1 ni le 2. Il ne leur reste donc que 7 stands. Pour BD, il restera 6 stands, pour BE 5,... il n’y a plus de stand possible pour BJ.
Hum, non ?
Tu exclus une possibilité pour B, et une pour C; mais effectivement 2 différentes pour BC, ce qui ne pose pas forcément problème.
Oui, j’ai raisonné trop vite sur les stands. C’est sur les créneaux que ça bloque.
_________________
« Les machines un jour pourront résoudre tous les problèmes, mais jamais aucune d'entre elles ne pourra en poser un ! »
Albert Einstein
 SeismiMineNiveau 5
SeismiMineNiveau 5
Autre option, rajouter des trous (et faire 10 ou 11 passages pour arriver aux 45 vrais affrontements)
Exemple pour n=4 :
AB CD
AD . .
. . BD
. . AC
BC . .
Cela augmente peut-être trop le nombre de tours (ici 5 au lieu de 3), cela dit.
Ou bien, tu rajoutes une 10e stand, et tu cherches à faire que chaque élève passe dans au moins 9 stands.
Ex : n=4
AB CD . .
. . AC BD
BC . . AD
B,C,D ont fait 2 stands, et A 3 stands.
Exemple pour n=4 :
AB CD
AD . .
. . BD
. . AC
BC . .
Cela augmente peut-être trop le nombre de tours (ici 5 au lieu de 3), cela dit.
Ou bien, tu rajoutes une 10e stand, et tu cherches à faire que chaque élève passe dans au moins 9 stands.
Ex : n=4
AB CD . .
. . AC BD
BC . . AD
B,C,D ont fait 2 stands, et A 3 stands.
 LotacheNiveau 2
LotacheNiveau 2
Wow, les cerveaux ont fusé pendant mon absence, merci à tous c'est vraiment sympa.
SeismiMine, c'est sûr que rajouter des tours résout le problème facilement mais ça ne sera pas une solution possible ici. Pareil pour le stand supplémentaire qui fait que certains passent à côté d'une activité.
Pour l'instant la seule piste ce serait celle de l'impossibilité à cause du nombre d'équipe, c'est bien ça? Donc si on veut quand même que chaque équipe essaie tous les stand et rencontre toutes les autres équipes, il faudrait partir sur 11 ou 9 équipes ? Je peux ajouter ou retirer un stand sans problème. Après on aura forcément toujours une équipe qui attend (j'aurais préféré éviter ce cas de figure mais si il le faut, ce n'est pas grave !)
11 équipes, 55 rencontres et 10 stands OU 9 équipes, 36 rencontres et 8 stands. Ca fonctionnerait?
SeismiMine, c'est sûr que rajouter des tours résout le problème facilement mais ça ne sera pas une solution possible ici. Pareil pour le stand supplémentaire qui fait que certains passent à côté d'une activité.
Pour l'instant la seule piste ce serait celle de l'impossibilité à cause du nombre d'équipe, c'est bien ça? Donc si on veut quand même que chaque équipe essaie tous les stand et rencontre toutes les autres équipes, il faudrait partir sur 11 ou 9 équipes ? Je peux ajouter ou retirer un stand sans problème. Après on aura forcément toujours une équipe qui attend (j'aurais préféré éviter ce cas de figure mais si il le faut, ce n'est pas grave !)
11 équipes, 55 rencontres et 10 stands OU 9 équipes, 36 rencontres et 8 stands. Ca fonctionnerait?
 EolullNiveau 3
EolullNiveau 3
Bonjour @Lotache ,
mon programme a trouvé une solution (quasiment instantanément), sauf si je n'ai pas compris la consigne :
1 AB CD EF GH IJ
2 AC BD EG FI HJ
3 AD BC EH FJ GI
4 AE BF CG DJ HI
5 AF BE CH DI GJ
6 AG BH CI DF EJ
7 AH BI CJ DE FG
8 AI BJ CE DG FH
9 AJ BG CF DH EI
mon programme a trouvé une solution (quasiment instantanément), sauf si je n'ai pas compris la consigne :
1 AB CD EF GH IJ
2 AC BD EG FI HJ
3 AD BC EH FJ GI
4 AE BF CG DJ HI
5 AF BE CH DI GJ
6 AG BH CI DF EJ
7 AH BI CJ DE FG
8 AI BJ CE DG FH
9 AJ BG CF DH EI
 ylmExpert spécialisé
ylmExpert spécialisé
Je crois que tu n'as pas compris la consigne : tu ne prends pas en compte les stands.Kanpindon a écrit:Bonjour @Lotache ,
mon programme a trouvé une solution (très rapidement), sauf si je n'ai pas compris la consigne :
1 AB CD EF GH IJ
2 AC BD EG FI HJ
3 AD BC EH FJ GI
4 AE BF CG DJ HI
5 AF BE CH DI GJ
6 AG BH CI DF EJ
7 AH BI CJ DE FG
8 AI BJ CE DG FH
9 AJ BG CF DH EI
_________________
The life of man, solitary, poor, nasty, brutish and short.
Thomas Hobbes
 EnaecoVénérable
EnaecoVénérable
A ne peut pas être simultanément au stand 1 et au stand 2 (et a fortiori aux 7 autres stands)
Page 1 sur 2 • 1, 2 

Permission de ce forum:
Vous ne pouvez pas répondre aux sujets dans ce forum



