Page 1 sur 2 • 1, 2 

 Manu7Expert spécialisé
Manu7Expert spécialisé
Je me demande pourquoi les définitions des quadrilatères particuliers (surtout le losange et le rectangle) sont souvent fausses dans les fiches visibles sur internet et utilisées par certains PE ainsi que dans certains manuels.
Exemple classique : "Un losange est un quadrilatère qui a 4 côtés égaux et pas d'angles droits"
De plus, il y a aussi de nombreuses erreurs dans les exercices comme dans un exercice répandu sur les quadrilatères "Jeu du portrait" où il y a en général plusieurs réponses possibles mais on devine qu'une seule sera admise.
Pourtant les définitions sont simples :
Un parallélogramme est un quadrilatère qui a ses côtés opposés parallèles.
Un rectangle est un quadrilatère qui a quatre angles droits.
Un losange est un quadrilatère qui a quatre côtés de même longueur.
Un carré est un quadrilatère qui a quatre angles droits et quatre côtés de même longueur.
En plus, il y a un avantage par rapport aux définitions fausses, elles sont plus courtes et plus faciles à apprendre.
Je relativise, la grande majorité des PE utilisent les bonnes définitions. Mais je me demande pourquoi on voit des erreurs dans ce domaine. Ce problème est connu, c'est dommage que dans les programmes on ne rappelle pas les bonnes définitions.
Exemple classique : "Un losange est un quadrilatère qui a 4 côtés égaux et pas d'angles droits"
De plus, il y a aussi de nombreuses erreurs dans les exercices comme dans un exercice répandu sur les quadrilatères "Jeu du portrait" où il y a en général plusieurs réponses possibles mais on devine qu'une seule sera admise.
Pourtant les définitions sont simples :
Un parallélogramme est un quadrilatère qui a ses côtés opposés parallèles.
Un rectangle est un quadrilatère qui a quatre angles droits.
Un losange est un quadrilatère qui a quatre côtés de même longueur.
Un carré est un quadrilatère qui a quatre angles droits et quatre côtés de même longueur.
En plus, il y a un avantage par rapport aux définitions fausses, elles sont plus courtes et plus faciles à apprendre.
Je relativise, la grande majorité des PE utilisent les bonnes définitions. Mais je me demande pourquoi on voit des erreurs dans ce domaine. Ce problème est connu, c'est dommage que dans les programmes on ne rappelle pas les bonnes définitions.
 William FosterExpert
William FosterExpert
Sans doute parce que les gens sont habitués à une vision cloisonnée (et excluante) plutôt qu'une vision ensembliste (et incluante).
Certains PE ont bien du mérite à donner des définitions justes et pertinentes, alors qu'ils sont régulièrement abreuvés de trucs faux vivement proposés par les Conseillers de Circonscription et/ou l'ESPE...
Un des exemples les plus classiques de cette erreur est la description qui est faite du panneau "Itinéraire prioritaire" qui serait un losange, car pointe en bas...
Certains PE ont bien du mérite à donner des définitions justes et pertinentes, alors qu'ils sont régulièrement abreuvés de trucs faux vivement proposés par les Conseillers de Circonscription et/ou l'ESPE...

Un des exemples les plus classiques de cette erreur est la description qui est faite du panneau "Itinéraire prioritaire" qui serait un losange, car pointe en bas...
_________________
Tout le monde me dit que je ne peux pas faire l'unanimité.
"Opinions are like orgasms : mine matters most and I really don't care if you have one." Sylvia Plath
Vérificateur de miroir est un métier que je me verrais bien faire, un jour.
 JPhMMDemi-dieu
JPhMMDemi-dieu
J'ai déjà lu un : "Si un quadrilatère a deux côtés parallèles et de même longueur, alors c'est un parallélogramme".


- Spoiler:
- Et s'il est croisé, patate ?
_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
 William FosterExpert
William FosterExpert
Peut-être une forme d'évolution ultime comme pour certains pokemon.
Et le losange correspondrait à une évolution de niveau 2 du quadrilatère de base, tout comme le rectangle mais dans une autre branche.
Du coup, un quadrilatère qui serait à la fois losange et rectangle n'est pas envisageable car ne correspond pas à la nomenclature pokemon.
Et le losange correspondrait à une évolution de niveau 2 du quadrilatère de base, tout comme le rectangle mais dans une autre branche.
Du coup, un quadrilatère qui serait à la fois losange et rectangle n'est pas envisageable car ne correspond pas à la nomenclature pokemon.
_________________
Tout le monde me dit que je ne peux pas faire l'unanimité.
"Opinions are like orgasms : mine matters most and I really don't care if you have one." Sylvia Plath
Vérificateur de miroir est un métier que je me verrais bien faire, un jour.
 JPhMMDemi-dieu
JPhMMDemi-dieu
:missT2:William Foster a écrit:Peut-être une forme d'évolution ultime comme pour certains pokemon.
Et le losange correspondrait à une évolution de niveau 2 du quadrilatère de base, tout comme le rectangle mais dans une autre branche.
Du coup, un quadrilatère qui serait à la fois losange et rectangle n'est pas envisageable car ne correspond pas à la nomenclature pokemon.
Tu es l'un de mes sixièmes ?
_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
 dami1kdHabitué du forum
dami1kdHabitué du forum
EmmanuelB a écrit:Je me demande pourquoi les définitions des quadrilatères particuliers (surtout le losange et le rectangle) sont souvent fausses dans les fiches visibles sur internet et utilisées par certains PE ainsi que dans certains manuels.
Exemple classique : "Un losange est un quadrilatère qui a 4 côtés égaux et pas d'angles droits"
De plus, il y a aussi de nombreuses erreurs dans les exercices comme dans un exercice répandu sur les quadrilatères "Jeu du portrait" où il y a en général plusieurs réponses possibles mais on devine qu'une seule sera admise.
Pourtant les définitions sont simples :
Un parallélogramme est un quadrilatère qui a ses côtés opposés parallèles.
Un rectangle est un quadrilatère qui a quatre angles droits.
Un losange est un quadrilatère qui a quatre côtés de même longueur.
Un carré est un quadrilatère qui a quatre angles droits et quatre côtés de même longueur.
En plus, il y a un avantage par rapport aux définitions fausses, elles sont plus courtes et plus faciles à apprendre.
Je relativise, la grande majorité des PE utilisent les bonnes définitions. Mais je me demande pourquoi on voit des erreurs dans ce domaine. Ce problème est connu, c'est dommage que dans les programmes on ne rappelle pas les bonnes définitions.
D'autres se sont posés la même question et ont le mérite d'avoir clarifié les choses dans ce document eduscol paru le mois dernier : http://cache.media.eduscol.education.fr/file/Geometrie/38/5/RA16_C3_MATH_Espace-geometrie_897385.pdf
En particulier, les annexes fournissent une fois pour toute des définitions acceptables !
Concernant les erreurs des PE, cela vient du fait que tous n'ont pas une formation scientifique de base et certains ne sont pas eux-même au clair avec losange/carré/rectangle. J'ai déjà vu des mémoires sur la géométrie où l'on exclut le carré des losanges ! Cela va dans le même sens qu'un document qui doit rappeler la différence entre être et avoir...
 JPhMMDemi-dieu
JPhMMDemi-dieu
Le copier/coller a encore, cependant, fait des ravages.
http://cache.media.education.gouv.fr/file/Geometrie/40/3/RA16_C3_MATH_Espace-geometrie_disque-cercle_897403.pdf

Regarder :
(*) L'arc AB passant par C.
(*) Un arc AB.
(*) Le rayon [OA] (dont le texte ne veut à peu près rien dire, et la distinction entre le rayon d'un cercle (un nombre, donc) et un rayon d'un cercle (un segment, donc) est tout à fait absente, mais on y fait bien la distinction entre un rayon et le rayon [OA])
Bref, tout cela me semble fort confus. Suffisamment pour embrouiller l'esprit de quelqu'un qui n'est pas au clair avec tout cela (les autres n'ayant pas besoin du document).
http://cache.media.education.gouv.fr/file/Geometrie/40/3/RA16_C3_MATH_Espace-geometrie_disque-cercle_897403.pdf

Regarder :
(*) L'arc AB passant par C.
(*) Un arc AB.
(*) Le rayon [OA] (dont le texte ne veut à peu près rien dire, et la distinction entre le rayon d'un cercle (un nombre, donc) et un rayon d'un cercle (un segment, donc) est tout à fait absente, mais on y fait bien la distinction entre un rayon et le rayon [OA])
Bref, tout cela me semble fort confus. Suffisamment pour embrouiller l'esprit de quelqu'un qui n'est pas au clair avec tout cela (les autres n'ayant pas besoin du document).
_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
 pseudo-intelloSage
pseudo-intelloSage
J'avoue que je n'ai rien compris à l'arc Ab passant par C.
Je sis ce qu'est un rayon, mais je n'aurais pas fait le distinguo avec LE rayon.
L4arc AB, je ne connaissais pas, mais à moins que je me goure, je comprends (enfin, je crois comprendre) et ça me paraît plus clair...
Je sis ce qu'est un rayon, mais je n'aurais pas fait le distinguo avec LE rayon.
L4arc AB, je ne connaissais pas, mais à moins que je me goure, je comprends (enfin, je crois comprendre) et ça me paraît plus clair...
_________________
- Publicité:
Mots croisés d'apprentissage - lecture et orthographe
Mamusique sur Bandcamp
Ecoutez mes chansons sur Soundcloud
 fifi51Fidèle du forum
fifi51Fidèle du forum
C'est assez mal dit, effectivement.
Intuitivement, j'ai l'impression d'avoir un document (mal) traduit .
Intuitivement, j'ai l'impression d'avoir un document (mal) traduit .
_________________
Oui, j'ai un clavier Fisher Price pour l'instant !
 JPhMMDemi-dieu
JPhMMDemi-dieu
Très juste.fifi51 a écrit:Intuitivement, j'ai l'impression d'avoir un document (mal) traduit .
_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
 vincesirNiveau 2
vincesirNiveau 2
Ce qui est donné dans la figure est correct malgré quelques formulations litigieuses. Pour répondre à vos interrogations, on parle d'"un" rayon pour définir un segment d'extrémité un point du cercle (n'importe lequel) et son centre, le rayon [OA] pour indiquer que c'est le segment qui relie le centre et le point A appartenant au cercle, et on dit "le" rayon pour définir la longueur commune aux rayons. La même chose sur le diamètre (à la fois segment ou longueur selon le déterminant défini ou indéfini).
Pour les arcs, si tu places deux points sur un cercle, tu as donc deux possibilités pour les joindre selon le chemin emprunté : si ça ne prête pas à confusion ou que ça n'a pas d'importance, on note AB avec un arc sinon, on précise par quel point cela passe.
Le problème de la figure, c'est que toutes les définitions sont données sur une même figure, en principe, on ne détaille que certains points sur la figure puis dans les définitions on précise certains points, par ex, un ou le rayon...
Pour les arcs, si tu places deux points sur un cercle, tu as donc deux possibilités pour les joindre selon le chemin emprunté : si ça ne prête pas à confusion ou que ça n'a pas d'importance, on note AB avec un arc sinon, on précise par quel point cela passe.
Le problème de la figure, c'est que toutes les définitions sont données sur une même figure, en principe, on ne détaille que certains points sur la figure puis dans les définitions on précise certains points, par ex, un ou le rayon...
 mathmaxExpert spécialisé
mathmaxExpert spécialisé
Pour paraphraser en le contredisant Napoléon, je trouve que des définitions avec des mots valent mieux qu'un croquis surchargé.
_________________
« Les machines un jour pourront résoudre tous les problèmes, mais jamais aucune d'entre elles ne pourra en poser un ! »
Albert Einstein
 JPhMMDemi-dieu
JPhMMDemi-dieu
Quand on sait d'où vient le document et à quoi il est destiné, ce n'est guère rassurant.
_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
 MoonchildSage
MoonchildSage
EmmanuelB a écrit:Je me demande pourquoi les définitions des quadrilatères particuliers (surtout le losange et le rectangle) sont souvent fausses dans les fiches visibles sur internet et utilisées par certains PE ainsi que dans certains manuels.
Exemple classique : "Un losange est un quadrilatère qui a 4 côtés égaux et pas d'angles droits"
De plus, il y a aussi de nombreuses erreurs dans les exercices comme dans un exercice répandu sur les quadrilatères "Jeu du portrait" où il y a en général plusieurs réponses possibles mais on devine qu'une seule sera admise.
Pourtant les définitions sont simples :
Un parallélogramme est un quadrilatère qui a ses côtés opposés parallèles.
Un rectangle est un quadrilatère qui a quatre angles droits.
Un losange est un quadrilatère qui a quatre côtés de même longueur.
Un carré est un quadrilatère qui a quatre angles droits et quatre côtés de même longueur.
En plus, il y a un avantage par rapport aux définitions fausses, elles sont plus courtes et plus faciles à apprendre.
Je relativise, la grande majorité des PE utilisent les bonnes définitions. Mais je me demande pourquoi on voit des erreurs dans ce domaine. Ce problème est connu, c'est dommage que dans les programmes on ne rappelle pas les bonnes définitions.
Est-ce qu'on s'autorise les quadrilatères aplatis ? Parce que si c'est le cas alors la définition du parallélogramme pose problème.
 JPhMMDemi-dieu
JPhMMDemi-dieu
A cause des côtés opposés ?Moonchild a écrit:Est-ce qu'on s'autorise les quadrilatères aplatis ? Parce que si c'est le cas alors la définition du parallélogramme pose problème.
_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
 MoonchildSage
MoonchildSage
JPhMM a écrit:A cause des côtés opposés ?Moonchild a écrit:Est-ce qu'on s'autorise les quadrilatères aplatis ? Parce que si c'est le cas alors la définition du parallélogramme pose problème.
Pas uniquement : l'écueil des côtés opposés peut être facilement contourné en posant comme convention que, pour le quadrilatère ABCD y compris aplati, on appelle côtés opposés [AB] et [CD] d'une part et [AD] et [BC] d'autre part.
Le principal problème est que si A, B, C et D sont quatre points alignés et distincts deux à deux, alors la droite (AB) est parallèle à la droite (CD) et la droite (AD) est parallèle à la droite (BC) et donc le quadrilatère ABCD a bel et bien ses "côtés opposés" parallèles sans qu'il soit forcément ce qu'on appelle un parallélogramme aplati.
 JPhMMDemi-dieu
JPhMMDemi-dieu
En effet. J'ai compris ensuite ce que tu voulais dire : pour tout quadrilatère aplati, tous les côtés sont parallèles.
PS : la notion de côté elle-même mériterait d'être précisée dès lors que l'on parle de côtés parallèles.
PS : la notion de côté elle-même mériterait d'être précisée dès lors que l'on parle de côtés parallèles.
_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
 Manu7Expert spécialisé
Manu7Expert spécialisé
Un triangle plat est-il un triangle ?
Un parallélogramme aplati est-il un parallélogramme ?
Un quadrilatère aplati est-il un quadrilatère ?
Pour la notion de côté, je ne vois pas bien ce qui pourrait poser problème ?
Dans une leçon sur les quadrilatères niveau primaire et collège, il ne me semble pas utile d'envisager les quadrilatères aplatis et pourtant c'est intéressant d'en parler en disant qu'on ne les étudiera pas, cela attise la curiosité des élèves... On le voit bien quand on réalise un losange articulé, on s'intéresse finalement très rapidement aux deux cas particuliers (losange plat et carré)
Un parallélogramme aplati est-il un parallélogramme ?
Un quadrilatère aplati est-il un quadrilatère ?
Pour la notion de côté, je ne vois pas bien ce qui pourrait poser problème ?
Dans une leçon sur les quadrilatères niveau primaire et collège, il ne me semble pas utile d'envisager les quadrilatères aplatis et pourtant c'est intéressant d'en parler en disant qu'on ne les étudiera pas, cela attise la curiosité des élèves... On le voit bien quand on réalise un losange articulé, on s'intéresse finalement très rapidement aux deux cas particuliers (losange plat et carré)
 Manu7Expert spécialisé
Manu7Expert spécialisé
Les exercices où il y a des erreurs sont souvent du style suivant :
On donne plusieurs quadrilatères numérotés et il faut retrouver les rectangles, les losanges et les carrés.
Dans ce cas, il faut accepter qu'on puisse mettre les carrés dans la case losange. Parfois on refuse cette réponse.
Pourtant si on ajoute d'autres polygones et qu'on demande aussi les numéros des quadrilatères alors tout le monde acceptera aussi les losanges, les carrés et les rectangles.
Donc un élève peut parfaitement comprendre qu'un carré est un quadrilatère particulier. Alors il doit être capable de comprendre que c'est aussi un losange particulier.
Malheureusement, tout le monde n'est pas du même avis, on voit "parfois" des formateurs qui conseillent d'exclure le carré de la famille des losanges car c'est plus facile à comprendre pour les élèves.
On donne plusieurs quadrilatères numérotés et il faut retrouver les rectangles, les losanges et les carrés.
Dans ce cas, il faut accepter qu'on puisse mettre les carrés dans la case losange. Parfois on refuse cette réponse.
Pourtant si on ajoute d'autres polygones et qu'on demande aussi les numéros des quadrilatères alors tout le monde acceptera aussi les losanges, les carrés et les rectangles.
Donc un élève peut parfaitement comprendre qu'un carré est un quadrilatère particulier. Alors il doit être capable de comprendre que c'est aussi un losange particulier.
Malheureusement, tout le monde n'est pas du même avis, on voit "parfois" des formateurs qui conseillent d'exclure le carré de la famille des losanges car c'est plus facile à comprendre pour les élèves.
 JPhMMDemi-dieu
JPhMMDemi-dieu
Qui demande d’exclure les carrés des losanges dit une ânerie. Point barre.
_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
 Manu7Expert spécialisé
Manu7Expert spécialisé
Oui JPhMM, je suis d'accord, mais ce n'est pas simple à faire passer comme message par exemple dans des réunions de cycle 3 quand on a des documents "sérieux" qui disent le contraire.
 William FosterExpert
William FosterExpert
Le carré est un losange particulier.
Dire qu'un carré n'est pas un losange parce qu'il aurait un truc en plus, c'est comme dire qu'une fille qui aurait des cheveux longs n'est plus une fille, ou refuser de considérer comme êtres humains les gens qui portent des lunettes.

Edit : Je précise que le Bob est pour les formateurs et les documents sérieux qui disent n'imp'... Pas pour EmmanuelB
Dire qu'un carré n'est pas un losange parce qu'il aurait un truc en plus, c'est comme dire qu'une fille qui aurait des cheveux longs n'est plus une fille, ou refuser de considérer comme êtres humains les gens qui portent des lunettes.

Edit : Je précise que le Bob est pour les formateurs et les documents sérieux qui disent n'imp'... Pas pour EmmanuelB

_________________
Tout le monde me dit que je ne peux pas faire l'unanimité.
"Opinions are like orgasms : mine matters most and I really don't care if you have one." Sylvia Plath
Vérificateur de miroir est un métier que je me verrais bien faire, un jour.
 ycombeMonarque
ycombeMonarque
Fille à lunettes...William Foster a écrit:Le carré est un losange particulier.
Dire qu'un carré n'est pas un losange parce qu'il aurait un truc en plus, c'est comme dire qu'une fille qui aurait des cheveux longs n'est plus une fille, ou refuser de considérer comme êtres humains les gens qui portent des lunettes.
Et alors, de ce fait, une fille à cheveux long à lunettes ce serait quoi?

_________________
Assurbanipal: "Passant, mange, bois, divertis-toi ; tout le reste n’est rien".
Franck Ramus : "Les sciences de l'éducation à la française se font fort de produire un discours savant sur l'éducation, mais ce serait visiblement trop leur demander que de mettre leur discours à l'épreuve des faits".
 ycombeMonarque
ycombeMonarque
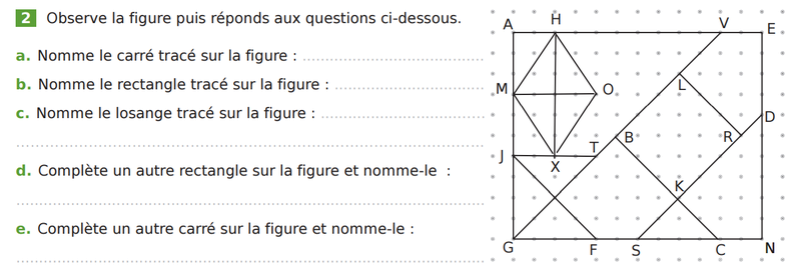
Pas besoin d'aller chercher des documents de primaire pour voir ce genre d'erreur.EmmanuelB a écrit:Les exercices où il y a des erreurs sont souvent du style suivant :
On donne plusieurs quadrilatères numérotés et il faut retrouver les rectangles, les losanges et les carrés.
Dans ce cas, il faut accepter qu'on puisse mettre les carrés dans la case losange. Parfois on refuse cette réponse.
Cahier Sesamath 2015 sixième, p 83, exercice 2.
http://manuel.sesamath.net/index.php?page=telechargement_6e_2015
_________________
Assurbanipal: "Passant, mange, bois, divertis-toi ; tout le reste n’est rien".
Franck Ramus : "Les sciences de l'éducation à la française se font fort de produire un discours savant sur l'éducation, mais ce serait visiblement trop leur demander que de mettre leur discours à l'épreuve des faits".
Page 1 sur 2 • 1, 2 

Permission de ce forum:
Vous ne pouvez pas répondre aux sujets dans ce forum



