Page 1 sur 4 • 1, 2, 3, 4 

 AndréCNiveau 9
AndréCNiveau 9
Bonsoir,
Aujourd'hui, une élève de sixième est passée au tableau et a posé la soustraction 20-12,5 avec une telle complexité qu'elle seule et une autre élève ayant appris cette technique ont compris sa méthode.
Elle parlait de casser le 0 du 20, puis a écrit un 10 en l'encerclant au dessus du chiffre des dixièmes (le 0) .
Au final, il y a eu 4 fois le nombre 10 encerclé et au bout de 2 minutes, la soustraction fut terminée.
Les autres élèves sont resté comme moi hébétés. Leurs regards angoissés me priaient de les délivrer de cette torture interminable. Ils ont alors dénoncé l'institutrice et l'école où cette méthode sévit au CM2 en étant heureux de ne pas pas l'avoir appris.
Trouvant cette technique trop lente, j'ai dit à ces élèves qu'ils devront apprendre une technique plus rapide. Plusieurs autres élèves sont passés au tableau pour expliquer la technique classique. Il a fallu un bon quart d'heure pour que ces élèves comprennent la nouvelle technique.
Je m'attends désormais au pire pour les divisions...
J'ai cherché sur le net cette méthode, j'ai vu des méthodes causant de cassage, mais aucune avec des 10 encerclés..
Qui la connaît ? Pouvez-vous l'illustrer ?
Pourquoi enseigner cette technique au CM2 ?
Aujourd'hui, une élève de sixième est passée au tableau et a posé la soustraction 20-12,5 avec une telle complexité qu'elle seule et une autre élève ayant appris cette technique ont compris sa méthode.
Elle parlait de casser le 0 du 20, puis a écrit un 10 en l'encerclant au dessus du chiffre des dixièmes (le 0) .
Au final, il y a eu 4 fois le nombre 10 encerclé et au bout de 2 minutes, la soustraction fut terminée.
Les autres élèves sont resté comme moi hébétés. Leurs regards angoissés me priaient de les délivrer de cette torture interminable. Ils ont alors dénoncé l'institutrice et l'école où cette méthode sévit au CM2 en étant heureux de ne pas pas l'avoir appris.
Trouvant cette technique trop lente, j'ai dit à ces élèves qu'ils devront apprendre une technique plus rapide. Plusieurs autres élèves sont passés au tableau pour expliquer la technique classique. Il a fallu un bon quart d'heure pour que ces élèves comprennent la nouvelle technique.
Je m'attends désormais au pire pour les divisions...
J'ai cherché sur le net cette méthode, j'ai vu des méthodes causant de cassage, mais aucune avec des 10 encerclés..
Qui la connaît ? Pouvez-vous l'illustrer ?
Pourquoi enseigner cette technique au CM2 ?
 YazilikayaNeoprof expérimenté
YazilikayaNeoprof expérimenté
Tiens, je n'ai jamais vu la méthode de cassage qu'au CE1 ou CE2. Au CM, c'est la technique classique.
 AndréCNiveau 9
AndréCNiveau 9
C'est ce que je me suis dit, certainement une façon de donner du sens au CE1.Yazilikaya a écrit:Tiens, je n'ai jamais vu la méthode de cassage qu'au CE1 ou CE2. Au CM, c'est la technique classique.
Il n'y a pas plus simple pour donner du sens en CE1 ou CE2 ?
 Ma'amÉrudit
Ma'amÉrudit
La maîtresse de mon fils en CE1 a prévu d'enseigner la méthode de la dizaine cassée et elle nous a plus ou moins interdit de leur montrer la méthode classique à la réunion de rentrée... 
Il va falloir que je me penche sur ce que fait celui qui est au CM2...

Il va falloir que je me penche sur ce que fait celui qui est au CM2...

 BoubouleDoyen
BoubouleDoyen
Qu'est-ce que vous appelez la technique classique ? Je viens de taper soustraction CM sous google et je m'interroge ;-)
 CeladonDemi-dieu
CeladonDemi-dieu
Ah la place des retenues dans la soustraction ! Que de beaux souvenirs !
 AndréCNiveau 9
AndréCNiveau 9
Celle qui est décrite ici : http://mamaitressedecm1.fr/?p=1698Bouboule a écrit:Qu'est-ce que vous appelez la technique classique ? Je viens de taper soustraction CM sous google et je m'interroge ;-)
 BoubouleDoyen
BoubouleDoyen
AndréC a écrit:Celle qui est décrite ici : http://mamaitressedecm1.fr/?p=1698Bouboule a écrit:Qu'est-ce que vous appelez la technique classique ? Je viens de taper soustraction CM sous google et je m'interroge ;-)
Ok, ça va, c'est celle que j'ai apprise à part que je ne mets pas le "+".
Et du coup, casser les dizaines, c'est quoi ? (juste curiosité, si pas le temps, tant pis pour moi)
 PrezboGrand Maître
PrezboGrand Maître
Bouboule a écrit:
Et du coup, casser les dizaines, c'est quoi ? (juste curiosité, si pas le temps, tant pis pour moi)
Ycombes avait posté cette vidéo (en anglais). La chanson "New math" de Tom Lehrer, avec la méthode par cassage illustrée.
(Je ne sais pas si c'est cette variante de la méthode dont parle AndréC.)
Pédagogiquement, j'ai l'impression que le but de la méthode est d'insister sur le sens de ce que l'on fait (on "casse" une dizaine en dix unités) au prix de manipulations moins pratiques.
Je pense que c'est un erreur, car acquérir un peu de fluidité dans la manipulation me semble précéder, la plupart du temps, la compréhension du sens. (Et cette obsession de "donner du sens" influe justement beaucoup nos programmes français...)
 BoubouleDoyen
BoubouleDoyen
Prezbo a écrit:Bouboule a écrit:
Et du coup, casser les dizaines, c'est quoi ? (juste curiosité, si pas le temps, tant pis pour moi)
Ycombes avait posté cette vidéo (en anglais). La chanson "New math" de Tom Lehrer, avec la méthode par cassage illustrée.
(Je ne sais pas si c'est cette variante de la méthode dont parle AndréC.)
Pédagogiquement, j'ai l'impression que le but de la méthode est d'insister sur le sens de ce que l'on fait (on "casse" une dizaine en dix unités) au prix de manipulations moins pratiques.
Je pense que c'est un erreur, car acquérir un peu de fluidité dans la manipulation me semble précéder, la plupart du temps, la compréhension du sens. (Et cette obsession de "donner du sens" influe justement beaucoup nos programmes français...)
Merci pour vos réponses.
Je suis d'accord avec la remarque.
 VerduretteModérateur
VerduretteModérateur
La "dizaine cassée" est très souvent utilisée en CE1. Cela permet aux élèves de comprendre qu'on "re-transforme" une dizaine en 10 unités parce qu'on ne peut pas calculer (62 - 45) 2 moins 5.
Lorsque je les récupère en CE2, je leur explique qu'ils vont faire des opérations avec des nombres de plus en plus grands. On ne peut donc plus utiliser cette technique et ils vont apprendre la "technique des grands". Pour appuyer mes dires, je pose une soustraction du genre 7503 - 4776 : là, j'entends : " 3 moins 6, on ne peut pas, alors on barre le zéro...", et ils se rendent compte que ça coince. En CE2, on ne sait pas enlever 1 dizaine à 0 dizaine ...
Des petits malins plus doués proposent d'écrire 749, mais le problème va se re-poser avec 7 ôté de 4... ça devient une usine à gaz.
Et là je sors ma méthode avec les retenues.
Sauf que sur l'exemple proposé en lien, une chose me gêne beaucoup : le modèle dit "j'écris une retenue, et j'abaisse le 1". Très bien, mais ... pourquoi ?
Avec mes élèves j'utilise la "dizaine cassée" d'abord en manipulation, puis en calcul posé
exemple : 63 - 27 mais je la "code" d'une manière différente, sans barrer.
7 ôté de 3, je ne peux pas , je vais prendre une dizaine, je peux calculer 7 ôté de 13 = 6
Mais attention : dans l'opération, je devais enlever 2 dizaines à 6 dizaines, mais je ne dois pas oublier cette dizaine que j'ai déjà enlevée, donc j'écris +1 à côté du 2 (chiffre des dizaines du terme inférieur) pour le "retenir" (ne pas l'oublier, c'est bien l'utilité d'une retenue, non ? ) Le "+1" est écrit nettement plus petit, il faut dire que je leur demande d'aérer énormément leurs opérations, en écrivant leurs chiffres sur les lignes verticales du cahier, et non dans les colonnes. C'est un combat, mais ça permet d'obtenir des opérations vraiment alignées.
Et lorsque je passe à la colonne des dizaines, je dis : 2 + 1 = 3, ôté de 6, 3
Je leur apprends en amont l'expression "ôté de" en allant du terme inférieur vers le terme supérieur, pour éviter d'entendre "6 moins 2 plus 1", ou 6 moins 2 (en oubliant la retenue).
Honnêtement, ça marche bien, ils sont fiers d'utiliser "une technique de grand", ce qui compense l'abandon du confort de la technique qu'ils connaissaient. Ce qui les gêne le plus, au début, c'est ce "ôté de" qu'ils ignorent. Je dis qu'ils peuvent aussi dire "pour aller à". L'écueil fréquent, c'est d'entendre , pour calculer 342 - 59 : 2 moins 9, je ne peux pas, donc je remplace par 9 - 2.
Ensuite, j'ai ceux qui, ayant appris la retenue, en mettent partout, même là où elles ne sont pas nécessaires, mais c'est pareil pour l'addition, et là encore, c'est une question d'entraînement. Je ne vous apprendrai rien en vous disant qu'il faut faire et refaire toutes choses, et petit à petit, ça rentre.
Deux dernières précisions : je leur demande de nommer ce qu'ils vont "prendre" pour faciliter leur calcul, exemple : 7 239 - 3 784 , 8 (d) ôté de 3(d), je ne peux pas, je prends une centaine : 8 ôté de 13 ...
Et je leur dis accessoirement que "3 moins 8" , on ne peut pas en CE2. Qu'ils apprendront à le faire au collège. J'évite de dire que c'est "impossible".
Lorsque je les récupère en CE2, je leur explique qu'ils vont faire des opérations avec des nombres de plus en plus grands. On ne peut donc plus utiliser cette technique et ils vont apprendre la "technique des grands". Pour appuyer mes dires, je pose une soustraction du genre 7503 - 4776 : là, j'entends : " 3 moins 6, on ne peut pas, alors on barre le zéro...", et ils se rendent compte que ça coince. En CE2, on ne sait pas enlever 1 dizaine à 0 dizaine ...
Des petits malins plus doués proposent d'écrire 749, mais le problème va se re-poser avec 7 ôté de 4... ça devient une usine à gaz.
Et là je sors ma méthode avec les retenues.
Sauf que sur l'exemple proposé en lien, une chose me gêne beaucoup : le modèle dit "j'écris une retenue, et j'abaisse le 1". Très bien, mais ... pourquoi ?
Avec mes élèves j'utilise la "dizaine cassée" d'abord en manipulation, puis en calcul posé
exemple : 63 - 27 mais je la "code" d'une manière différente, sans barrer.
7 ôté de 3, je ne peux pas , je vais prendre une dizaine, je peux calculer 7 ôté de 13 = 6
Mais attention : dans l'opération, je devais enlever 2 dizaines à 6 dizaines, mais je ne dois pas oublier cette dizaine que j'ai déjà enlevée, donc j'écris +1 à côté du 2 (chiffre des dizaines du terme inférieur) pour le "retenir" (ne pas l'oublier, c'est bien l'utilité d'une retenue, non ? ) Le "+1" est écrit nettement plus petit, il faut dire que je leur demande d'aérer énormément leurs opérations, en écrivant leurs chiffres sur les lignes verticales du cahier, et non dans les colonnes. C'est un combat, mais ça permet d'obtenir des opérations vraiment alignées.
Et lorsque je passe à la colonne des dizaines, je dis : 2 + 1 = 3, ôté de 6, 3
Je leur apprends en amont l'expression "ôté de" en allant du terme inférieur vers le terme supérieur, pour éviter d'entendre "6 moins 2 plus 1", ou 6 moins 2 (en oubliant la retenue).
Honnêtement, ça marche bien, ils sont fiers d'utiliser "une technique de grand", ce qui compense l'abandon du confort de la technique qu'ils connaissaient. Ce qui les gêne le plus, au début, c'est ce "ôté de" qu'ils ignorent. Je dis qu'ils peuvent aussi dire "pour aller à". L'écueil fréquent, c'est d'entendre , pour calculer 342 - 59 : 2 moins 9, je ne peux pas, donc je remplace par 9 - 2.
Ensuite, j'ai ceux qui, ayant appris la retenue, en mettent partout, même là où elles ne sont pas nécessaires, mais c'est pareil pour l'addition, et là encore, c'est une question d'entraînement. Je ne vous apprendrai rien en vous disant qu'il faut faire et refaire toutes choses, et petit à petit, ça rentre.
Deux dernières précisions : je leur demande de nommer ce qu'ils vont "prendre" pour faciliter leur calcul, exemple : 7 239 - 3 784 , 8 (d) ôté de 3(d), je ne peux pas, je prends une centaine : 8 ôté de 13 ...
Et je leur dis accessoirement que "3 moins 8" , on ne peut pas en CE2. Qu'ils apprendront à le faire au collège. J'évite de dire que c'est "impossible".
 AndréCNiveau 9
AndréCNiveau 9
Moi non plus.Bouboule a écrit:AndréC a écrit:Celle qui est décrite ici : http://mamaitressedecm1.fr/?p=1698Bouboule a écrit:Qu'est-ce que vous appelez la technique classique ? Je viens de taper soustraction CM sous google et je m'interroge ;-)
Ok, ça va, c'est celle que j'ai apprise à part que je ne mets pas le "+".
 YazilikayaNeoprof expérimenté
YazilikayaNeoprof expérimenté
Verdurette a très bien expliqué. Merci.
Manipulation/cassage/technique usuelle.
Mais effectivement, même avec ça, certains ont la tentation dans 352 - 128 de faire 8 - 2 au lieu de 2 - 8.
Manipulation/cassage/technique usuelle.
Mais effectivement, même avec ça, certains ont la tentation dans 352 - 128 de faire 8 - 2 au lieu de 2 - 8.
 AndréCNiveau 9
AndréCNiveau 9
Merci pour vos explications. Je vais demander à cet élève de refaire un exemple afin que vous voyez tous ces 10 encerclés qui obscurcissent la technique car on ne voit plus que cela. Il y en a partout !Verdurette a écrit:Sauf que sur l'exemple proposé en lien, une chose me gêne beaucoup : le modèle dit "j'écris une retenue, et j'abaisse le 1". Très bien, mais ... pourquoi ?
Avoir une technique avec des notations minimaliste permet justement de rester centrer sur le problème : combien doit-on ajouter à 12,5 pour trouver 20. C'est le sens de la soustraction.
Même si l'élève ne comprend pas toujours le pourquoi de la technicité, savoir qu'elle fonctionne et pouvoir vérifier qu'elle fonctionne avec une addition suffit au niveau du sens.
Comprendre le pourquoi de la technicité est une bonne chose, mais ce n'est pas essentiel. L'essentiel, c'est de comprendre le sens de la soustraction avant de comprendre le sens de sa technique.
Face à un problème l'essentiel, c'est de savoir s'il s'agit d'un problème d'addition, de soustraction, de multiplication ou de division.
Deuxième intérêt, la rapidité. A trop s'attarder sur les détails techniques, l'élève perd la finalité du problème initial. Le problème n'est plus le même, ce qui risque justement de lui faire perdre le fil de son raisonnement lorsque le problème comporte une succession d'opérations.
Etre rapide permet de ne pas perdre le sens du problème tout en permettant sa vérification par d'autres opérations. La lenteur technique nuit à la compréhension globale.
 VerduretteModérateur
VerduretteModérateur
AndréC a écrit:Comprendre le pourquoi de la technicité est une bonne chose, mais ce n'est pas essentiel. L'essentiel, c'est de comprendre le sens de la soustraction avant de comprendre le sens de sa technique.
Face à un problème l'essentiel, c'est de savoir s'il s'agit d'un problème d'addition, de soustraction, de multiplication ou de division.
Merci de me l'apprendre.

Cela me semble une évidence, mais je n'en ai pas parlé ici, puisqu'il était question de technique opératoire.
Je pars donc du principe que l'on a déjà travaillé le sens de la soustraction.
Mais je n'aime pas dire "on met une retenue" comme un truc automatique sans comprendre ce qu'elle signifie.
PS Le "+1", c'est au début. Ensuite on peut le supprimer, voire même supprimer les retenues, mais pour cela il faut déjà un bon entraînement.
 YazilikayaNeoprof expérimenté
YazilikayaNeoprof expérimenté
AndréC a écrit:Merci pour vos explications. Je vais demander à cet élève de refaire un exemple afin que vous voyez tous ces 10 encerclés qui obscurcissent la technique car on ne voit plus que cela. Il y en a partout !Verdurette a écrit:Sauf que sur l'exemple proposé en lien, une chose me gêne beaucoup : le modèle dit "j'écris une retenue, et j'abaisse le 1". Très bien, mais ... pourquoi ?
Avoir une technique avec des notations minimaliste permet justement de rester centrer sur le problème : combien doit-on ajouter à 12,5 pour trouver 20. C'est le sens de la soustraction.
Même si l'élève ne comprend pas toujours le pourquoi de la technicité, savoir qu'elle fonctionne et pouvoir vérifier qu'elle fonctionne avec une addition suffit au niveau du sens.
Comprendre le pourquoi de la technicité est une bonne chose, mais ce n'est pas essentiel. L'essentiel, c'est de comprendre le sens de la soustraction] avant de comprendre le sens de sa technique.
Face à un problème l'essentiel, c'est de savoir s'il s'agit d'un problème d'addition, de soustraction, de multiplication ou de division.
Deuxième intérêt, la rapidité. A trop s'attarder sur les détails techniques, l'élève perd la finalité du problème initial. Le problème n'est plus le même, ce qui risque justement de lui faire perdre le fil de son raisonnement lorsque le problème comporte une succession d'opérations.
Etre rapide permet de ne pas perdre le sens du problème tout en permettant sa vérification par d'autres opérations. La lenteur technique nuit à la compréhension globale.
Eh bien c'est une très grosse partie du travail fait en école élémentaire
 jaybeNiveau 9
jaybeNiveau 9
Le sujet de la technique de soustraction par cassage a déjà été abordé sur ce forum...
_________________
Les mathématiciens ne sont pas des gens qui trouvent les mathématiques faciles ; comme tout le monde, ils savent qu'elles sont difficiles, mais ça ne leur fait pas peur !
 InvitéInvité
InvitéInvité
Et vous avez regardé comment ils procèdent dans la méthode de Singapour ? 

 VerduretteModérateur
VerduretteModérateur
..............3 12
4 2
- 1 7
____________
2 5
Ce qui , comme la technique où on barre, est simple pour de petits nombres, mais un peu chargée pour les grands nombres.
J'ai essayé de décaler pour aligner les chiffres verticalement, mais ça ne marche pas très bien. C'est pour cela que j'ai mis des points avant 3 et 12 (3 d + 12)
On doit barrer de manière oblique.
- 1 7
____________
2 5
Ce qui , comme la technique où on barre, est simple pour de petits nombres, mais un peu chargée pour les grands nombres.
J'ai essayé de décaler pour aligner les chiffres verticalement, mais ça ne marche pas très bien. C'est pour cela que j'ai mis des points avant 3 et 12 (3 d + 12)
On doit barrer de manière oblique.
 BrindIfFidèle du forum
BrindIfFidèle du forum
J'avais assisté à une séquence de maths en 3rd grade (CE2 américain) où les élèves faisaient un bruit d'alarme lorsqu'on ne pouvait pas soustraire, une sorte d'« alerte à la retenue ». Ils étaient de ce fait super vigilants, car voulaient être les premiers à pouvoir le signaler, c'était amusant à observer (et impressionnant, car derrière ça l'instit ramenait très bien tout au calme).Verdurette a écrit:Honnêtement, ça marche bien, ils sont fiers d'utiliser "une technique de grand", ce qui compense l'abandon du confort de la technique qu'ils connaissaient. Ce qui les gêne le plus, au début, c'est ce "ôté de" qu'ils ignorent. Je dis qu'ils peuvent aussi dire "pour aller à". L'écueil fréquent, c'est d'entendre , pour calculer 342 - 59 : 2 moins 9, je ne peux pas, donc je remplace par 9 - 2.
Ensuite, j'ai ceux qui, ayant appris la retenue, en mettent partout, même là où elles ne sont pas nécessaires, mais c'est pareil pour l'addition, et là encore, c'est une question d'entraînement. Je ne vous apprendrai rien en vous disant qu'il faut faire et refaire toutes choses, et petit à petit, ça rentre.
Deux dernières précisions : je leur demande de nommer ce qu'ils vont "prendre" pour faciliter leur calcul, exemple : 7 239 - 3 784 , 8 (d) ôté de 3(d), je ne peux pas, je prends une centaine : 8 ôté de 13 ...
Je viens de poser la question à une élève de CM1... elle ne connaît pas les retenues, elle a fait une première tentative sans y arriver, a réalisé d'elle-même que ça ne collait pas et a recommencé en « cassant » le 0, puis le 5, pour pouvoir soustraire le 6. Et j'ai réalisé que je fais pareil lorsque j'ai besoin de calculer une soustraction, que ce soit de tête ou en calcul posé.Lorsque je les récupère en CE2, je leur explique qu'ils vont faire des opérations avec des nombres de plus en plus grands. On ne peut donc plus utiliser cette technique et ils vont apprendre la "technique des grands". Pour appuyer mes dires, je pose une soustraction du genre 7503 - 4776 : là, j'entends : " 3 moins 6, on ne peut pas, alors on barre le zéro...", et ils se rendent compte que ça coince. En CE2, on ne sait pas enlever 1 dizaine à 0 dizaine ...
Des petits malins plus doués proposent d'écrire 749, mais le problème va se re-poser avec 7 ôté de 4... ça devient une usine à gaz.
 AndréCNiveau 9
AndréCNiveau 9
Où ?jaybe a écrit:Le sujet de la technique de soustraction par cassage a déjà été abordé sur ce forum...
 AndréCNiveau 9
AndréCNiveau 9
Voici comment la soustraction 20 - 12,5 a été posée et effectuée par cette élève de sixième.
Les ratures font toutes partie intégrante de son calcul, excepté celle du résultat où elle s'est trompée et a corrigé son erreur.
Edit : image en plus grande
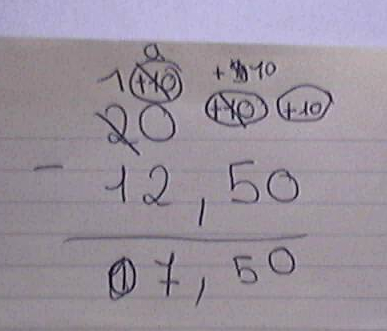
Les ratures font toutes partie intégrante de son calcul, excepté celle du résultat où elle s'est trompée et a corrigé son erreur.
Edit : image en plus grande
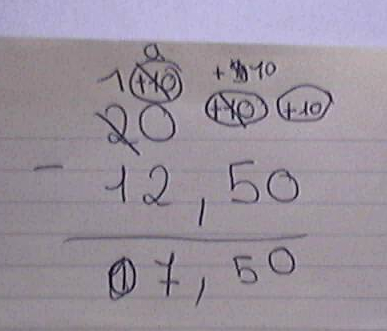
 fifi51Fidèle du forum
fifi51Fidèle du forum
 BoubouleDoyen
BoubouleDoyen
AndréC a écrit:Voici comment la soustraction 20 - 12,5 a été posée et effectuée par cette élève de sixième.
Les ratures font toutes partie intégrante de son calcul, excepté celle du résultat où elle s'est trompée et a corrigé son erreur.
Edit : image en plus grande
Ouh la la :-(
Question annexe : à partir de quel niveau peut-on attendre que (20 - 12,5) se fasse de tête ?
Page 1 sur 4 • 1, 2, 3, 4 

Permission de ce forum:
Vous ne pouvez pas répondre aux sujets dans ce forum



