Domaine de dérivabilité.

ernestin a écrit:Il y a un théorème dit « de prolongement par continuité » qui permet d'assurer que si une fonction est continue et dérivable de dérivée continue sur un intervalle ]a,b[ (a et b deux réels), alors la dérivée existe en a et en b.

Ben non : sqrt(x) par exemple.

pignolo a écrit:

ernestin a écrit:Il y a un théorème dit « de prolongement par continuité » qui permet d'assurer que si une fonction est continue et dérivable de dérivée continue sur un intervalle ]a,b[ (a et b deux réels), alors la dérivée existe en a et en b.

Ben non : sqrt(x) par exemple.

oui merci je me suis emmêlé les pinceaux.

Le théorème est celui là : f:]a,b[->|R est dérivable. Si lim(x->a)f'(x) existe et est égale à l, alors f est prolongeable par continuité sur [a,b[ et la fonction f prolongée sur [a,b[ est dérivable en a et sa dérivée est f'(a).

Alors je tiens à présenter mes excuses pour le truc sans intérêt que j'ai écrit page 2. Oui, j'avoue, j'ai écrit intervalle connexe alors que je voulais parler d'intervalle et que j'avais en tête connexe. J'ai honte

Hélips a écrit:Alors je tiens à présenter mes excuses pour le truc sans intérêt que j'ai écrit page 2. Oui, j'avoue, j'ai écrit intervalle connexe alors que je voulais parler d'intervalle et que j'avais en tête connexe. J'ai honte

nan mais tu sais, faut pas avoir honte, avec la fatigue, tout le monde peut dire n'importe quoi.

confession:

ben2510 a écrit:Mais la subtilité locale permet de mettre en perspective la platitude globale, non ?

Bof.
A quoi sert une dérivée aujourd'hui en lycée ?
A déterminer des variations.
Du coup, la singularité ponctuelle, pour aussi fondamentale qu'elle sera à plus haut niveau, me semble difficile à voir comme une nécessité par nos élèves.

Hélips a écrit:Alors je tiens à présenter mes excuses pour le truc sans intérêt que j'ai écrit page 2. Oui, j'avoue, j'ai écrit intervalle connexe alors que je voulais parler d'intervalle et que j'avais en tête connexe. J'ai honte

C'est très mal.
Heureusement que je n'avais pas mon arc.

Igniatius a écrit:Justement non, mon opinion est que ce n'est pas le "mieux a faire" : les TS ont tellement de mal à dériver une fonction basique et à étudier le signe de cette dérivée qu'il me semble presque contre-productif (au sens prématuré) d'aborder trop d'études de fonctions exotiques.
Ça me déprime d'arriver a penser cela mais il faut bien s'adapter !

Je partage malheureusement ce constat.

Igniatius a écrit:

francois75 a écrit:Que pensez-vous de la fonction comme exemple en 1e S ?
On y voit que la fonction est dérivable sur lorsque l'on applique le théorème de la dérivée du produit de deux fonctions, mais qu'elle est bien dérivable en 0 lorsque l'on calcule la limite du tx d'accroissement de f en 0.

Oui, c'est l'exemple déjà donné deux fois : il est classique et intéressant pour de bons élèves mais j'avoue ne plus en voir l'intérêt en 1S.
JE veux juste qu'ils pigent bien ce qu'est une dérivée avant d'aller s'intéresser à des subtilités locales.

Je fais encore cet exemple en exercice en première S (parfois en remplaçant x par un polynôme dans lequel on peut factoriser x) pour faire observer que le théorème de dérivation d'un produit ne permet pas de conclure à la non-dérivabilité lorsque l'un des facteurs n'est pas dérivable, mais c'est presque toujours un grand moment de solitude et en général, après avoir eu l'impression de perdre du temps, je n'en reparle plus du tout par la suite.
Je n'aborde même plus cette question en terminale car l'urgence est alors d'essayer apprendre aux élèves à calculer correctement une dérivée en vue du bac ; et, à ce moment-là, je maudis cet imbécile de collègue qui l'année précédente a perdu du temps à leur faire étudier la dérivabilité en 0 de   alors que beaucoup d'entre eux dérivent un produit en faisant le produit des dérivées.

Il me semble que c'est important de leur montrer cette histoire de x->x\sqrt(x) pas tellement pour des histoires de dérivabilité (je partage l'avis de ceux qui disent que ça parait aux élèves de la sodomie de diptères non consentants), mais pour des histoires de raisonnement.
Si on arrive à leur faire comprendre que le théorème dit "si ça alors paf" mais pas que "si pas ça alors pas paf", on fait un peu de math.

Hélips a écrit:Il me semble que c'est important de leur montrer cette histoire de x->x\sqrt(x) pas tellement pour des histoires de dérivabilité (je partage l'avis de ceux qui disent que ça parait aux élèves de la sodomie de diptères non consentants), mais pour des histoires de raisonnement.
Si on arrive à leur faire comprendre que le théorème dit "si ça alors paf" mais pas que "si pas ça alors pas paf", on fait un peu de math.

On n'apprend plus : "si ça alors paf" <=> "si pas paf alors pas ça" (alors qu'on dirait du Freud !)
Pardon pour le HS

Moonchild a écrit:
(...) alors que beaucoup d'entre eux dérivent un produit en faisant le produit des dérivées.

Ah bon c'est pas ça ? Il y a une autre méthode ? :lol: :lol: :lol: :lol: :lol:

RogerMartin a écrit:

Hélips a écrit:Il me semble que c'est important de leur montrer cette histoire de x->x\sqrt(x) pas tellement pour des histoires de dérivabilité (je partage l'avis de ceux qui disent que ça parait aux élèves de la sodomie de diptères non consentants), mais pour des histoires de raisonnement.
Si on arrive à leur faire comprendre que le théorème dit "si ça alors paf" mais pas que "si pas ça alors pas paf", on fait un peu de math.

On n'apprend plus : "si ça alors paf" <=> "si pas paf alors pas ça" (alors qu'on dirait du Freud !)
Pardon pour le HS

Si si. Dans mon collège l'an dernier on parle de "réciproque" et "contraposée" dès la 6e. Et franchement, j'ai vu la différence en 4e sur les 3 collèges où j'étais.

Sinon, je rejoins Mrs Hobie, je régresse à une allure impressionnante alors que je suis tout jeune, j'enseigne depuis 4ans. Finalement, je n'ai pas fait de maths "poussés" depuis 6ans (En licence 3). Car en Master de l'enseignement on s'est contenté de travailler les programmes, les leçons et la psycho d'ado... Et après 3ans de collège j'ai une grosse remise à niveau à faire. Heureusement que ce forum existe, il me rassure un peu parfois.

Fritz a écrit:Si si. Dans mon collège l'an dernier on parle de "réciproque" et "contraposée" dès la 6e. Et franchement, j'ai vu la différence en 4e sur les 3 collèges où j'étais.

En discutant avec une vraie bonne psy, en faisant le constat qu'au collège, la 4ème c'est l'horreur, et la cata mathématique ... elle m'expliquait qu'en fait c'est pile poile le moment où la majorité des ados ne sont physiologiquement pas aptes à comprendre ce qu'on leur demande de comprendre car les hormones remodèlent le cerveau ... faudrait faire avant ou après, en fait ... ce que tu sembles confirmer.
Mais par ailleurs en principe au lycée, les hormones ne rentrent plus en ligne de compte ...

et pour revenir aux tableaux de variations, il parait que "ça n'est pas grave de laisser vide quand on ne sait pas, puisqu'il n'y a plus les limites".
Graoumpfff.

Passées les bornes y'a plus de limite

Hélips a écrit:Alors je tiens à présenter mes excuses pour le truc sans intérêt que j'ai écrit page 2. Oui, j'avoue, j'ai écrit intervalle connexe alors que je voulais parler d'intervalle et que j'avais en tête connexe. J'ai honte

Tu pensais connexe ou connexe par arc?

Pour ma part j'essaie toujours de relier le calcul de la dérivée à la recherche de tangente à la courbe, dont découle les variations. Certains se rappellent que si y=ax+b et a>0 alors y est croissante ^^.

Mrs Hobie a écrit:

Fritz a écrit:Si si. Dans mon collège l'an dernier on parle de "réciproque" et "contraposée" dès la 6e. Et franchement, j'ai vu la différence en 4e sur les 3 collèges où j'étais.

En discutant avec une vraie bonne psy, en faisant le constat qu'au collège, la 4ème c'est l'horreur, et la cata mathématique ... elle m'expliquait qu'en fait c'est pile poile le moment où la majorité des ados ne sont physiologiquement pas aptes à comprendre ce qu'on leur demande de comprendre car les hormones remodèlent le cerveau ... faudrait faire avant ou après, en fait ... ce que tu sembles confirmer.
Mais par ailleurs en principe au lycée, les hormones ne rentrent plus en ligne de compte ...

et pour revenir aux tableaux de variations, il parait que "ça n'est pas grave de laisser vide quand on ne sait pas, puisqu'il n'y a plus les limites".
Graoumpfff.

C'est vraiment étrange : pourquoi des dizaines de générations n'ont pas eu de problèmes pour apprendre ces concepts et pourquoi maintenant ils ne pourraient pas... J'ai une idée lumineuse : 3 h 30 de maths par semaine c'est insuffisant pour apprendre correctement le programme de mathématique de 4eme, c'est la seule chose que l'on peut constater. Je part certes du postulat qu'en moyenne nos ados sont aussi intelligents que nous en moyenne à notre époque ( ce qui reste à prouver ).

Peut-être justement parce qu'on abordait certaines notions plus tôt ? Cela me rappelle la division posée :

Un jour on m'a expliqué que le cerveau de l'enfant ne pouvait pas appréhender l'algorithme de la division avant 11 ans. J'ai répondu que je posais des divisions à 7 ans. Ah oui, mais horreur je ne comprenais pas ce que je faisais ! Je reproduisais bêtement une technique. Et, si c'est vrai (je ne me rappelle pas), où est le problème ? J'ai compris plus tard, je ne vois pas en quoi posséder la technique aurait empêché une compréhension ultérieure. Au contraire, je pense que certaines acquisitions sollicitant la mémoire sont beaucoup faciles à un âge tendre, en particulier les tables de multiplication, ou les techniques de calcul. Mais cette injonction de ne rien faire avant d'avoir tout compris est contre-productive.

De nombreux intervenants dans la discussion proposent des exemples (ou des contrexemples) à base de racine carrée.
Aussi naturels soient ils, ces exemples ne sont pas tout à fait satisfaisants : au sens strict du terme, on ne peut pas parler de dérivée en 0 pour la fonction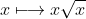 , mais seulement de dérivée à droite en 0. Il me semblerait plus judicieux d'utiliser la fonction racine cubique, qui, elle, est définie sur R. Ainsi, on peut vérifier que en dérivable, y compris en 0.

Naturellement, l'un ou l'autre exemple passera largement au delà de la compréhension de la plupart des élèves; mais l'utilisation de la racine cubique permet d'avoir la satisfaction de ne pas commettre d'abus de notation en parlant de dérivabilité dans un cas où il faudrait parler, au sens strict, de dérivabilité à droite.

Autre problème : dans tous les cas, la dérivée se calcule explicitement et a un sens, y compris en 0. Ainsi :

ce qui permet de conclure même sans utiliser le taux d'accroissement. Il suffit aux élèves d'utiliser le théorème de l'évidence : à partir du moment où on dispose d'une formule, la formule est vraie, même quand elle est fausse.

De ce point de vue, l'exemple que je proposais avec la fonction prolongé par continuité en 0 par f(0)=0 est plus consistant : la dérivée peut certes se calculer par une formule, mais cette formule est indéterminée en 0, donc le théorème de l'évidence ne s'applique pas dans ce cas.

Oui enfin la racine cubique en première, ça va piquer un peu...

Avatar des Abysses a écrit:C'est vraiment étrange : pourquoi des dizaines de générations n'ont pas eu de problèmes pour apprendre ces concepts et pourquoi maintenant ils ne pourraient pas... J'ai une idée lumineuse : 3 h  30 de maths par semaine c'est insuffisant pour apprendre correctement le programme de mathématique de 4eme, c'est la seule chose que l'on peut constater.

quand j'ai commencé y'a 15 ans, mes collègues disaient que la 4ème a toujours été la pire classe ...
Ensuite, les programmes ont en effet tellement évolué ... ainsi que la répartition horaire ... en tout cas il n'y a plus d'automatismes, et c'est fort dommage ...

Avatar des Abysses a écrit:Je part certes du postulat qu'en moyenne nos ados sont aussi intelligents que nous en moyenne à notre époque ( ce qui reste à prouver ).

ça me fait penser qu'il faut que je me penche sur l'effet Flynn ...
https://fr.wikipedia.org/wiki/Effet_Flynn

Hélips a écrit:Oui enfin la racine cubique en première, ça va piquer un peu...

Alors, ça, des fois, il y a des trucs qui passent bien, tu ne comprends pas pourquoi, des fois ... faut voir ...

mathmax a écrit:Peut-être justement parce qu'on abordait certaines notions plus tôt ? Cela me rappelle la division posée :

Un jour on m'a expliqué que le cerveau de l'enfant ne pouvait pas appréhender l'algorithme de la division avant 11 ans. J'ai répondu que je posais des divisions à 7 ans. Ah oui, mais horreur je ne comprenais pas ce que je faisais ! Je reproduisais bêtement une technique. Et, si c'est vrai (je ne me rappelle pas), où est le problème ? J'ai compris plus tard, je ne vois pas en quoi posséder la technique aurait empêché une compréhension ultérieure. Au contraire, je pense que certaines acquisitions sollicitant la mémoire sont beaucoup faciles à un âge tendre, en particulier les tables de multiplication, ou les techniques de calcul. Mais cette injonction de ne rien faire avant d'avoir tout compris est contre-productive.

Les mêmes gens qui pensent qu'on ne peut pas apprendre, et savoir faire, sans comprendre viennent au boulot le matin dans une voiture dont ils ignorent le fonctionnement du moteur, achètent un café à la machine sans comprendre comment le courant alterné qui sort de la prise murale est transformé en courant continu dans la boîte magique (ou comment la pièce de 1€ est transformée en café chaud), regardent leurs messages sur l'écran de leur smartphone sans savoir comment fonctionne un cristal, et passent leurs journées à donner leur avis grâce à leur ordi sans comprendre le fonctionnement des composants (puces, résistances, condensateurs, DD, proc, etc.) ou du réseau qu'ils utilisent. :|
Notons qu'ils ne comprennent pas non plus pourquoi je trouve qu'ils disent n'imp'... :lol:

Je sens cependant un (timide) retour en arrière pour les maths (histoire de revenir au post initial). Bien sûr, après avoir tant décrié l'apprentissage des tables de multiplication, hérésie pédagogique qui ne servait qu'à stigmatiser les pauvres apprenants qui n'apprenaient pas, nos penseurs ne pouvaient pas les remettre en l'état dans les nouveaux programmes. Nous parlerons donc de "Mémoriser des faits numériques et des procédures élémentaires de calcul." (cycle 3, p. 202)
Ce n'est qu'un début, continuons le combat... Ou l'inverse.

"Mémoriser des faits numériques et des procédures élémentaires de calcul."

Ils ont vraiment écrit ça ?

Je ne sais même pas ce que cela signifie.

mathmax a écrit:"Mémoriser des faits numériques et des procédures élémentaires de calcul."

Ils ont vraiment écrit ça ?

Programme de cycle 3 (p. 202) a écrit:Exemples de faits et procédures numériques :

» multiplier ou diviser par 10, par 100, par 1000 un nombre décimal,

» rechercher le complément à l’unité, à la dizaine, à la centaine supérieure,

» encadrer un nombre entre deux multiples consécutifs,

» trouver un quotient, un reste,

» multiplier par 5, par 25, par 50, par 100, par 0,1, par 0,5…

Personnellement, dans ces exemples, je ne vois que des procédures... J'en ai déduit (mais la question est sur mon calepin, prête à être posée en formation) que les "faits numériques" sont les tables.

Pour le fait religieux, je n'ai jamais cherché à comprendre ce que c'est exactement n'étant pas professeur d'histoire. Mais si ça vient chez nous, il va falloir s'y mettre ! Tu crois qu'ils enseignent des faits sportifs en EPS ?

Je crois que pour cerner la notion, il convient de se demander qu'est-ce qui n'est pas un fait numérique.

mathmax a écrit:Peut-être justement parce qu'on abordait certaines notions plus tôt ? Cela me rappelle la division posée :

Un jour on m'a expliqué que le cerveau de l'enfant ne pouvait pas appréhender l'algorithme de la division avant 11 ans. J'ai répondu que je posais des divisions à 7 ans. Ah oui, mais horreur je ne comprenais pas ce que je faisais ! Je reproduisais bêtement une technique. Et, si c'est vrai (je ne me rappelle pas), où est le problème ? J'ai compris plus tard, je ne vois pas en quoi posséder la technique aurait empêché une compréhension ultérieure. Au contraire, je pense que certaines acquisitions sollicitant la mémoire sont beaucoup faciles à un âge tendre, en particulier les tables de multiplication, ou les techniques de calcul. Mais cette injonction de ne rien faire avant d'avoir tout compris est contre-productive.

J'aime bien le "ON" de on m'a expliqué... Je pense plutôt que ce sont soit des personnes qui ont une théorie et qui trouvent des arguments pour que tout rentre dans leur théorie et/ou qui sont frustrés de ne pas avoir pu comprendre ces concepts à l'age de 7 ans. Je faisais des divisions ( certes simples et avec de petits nombres) à mon entrée en ce1. Le mode de fonctionnement est tout de même simple:

Nous sommes 4 nous avons 11 bonbons. Je distribue 1 bonbon a chacun puis je recommence. A la fin de la distribution, je constate que chacun de nous à 2 bonbons et il m'en reste 3. Après quelques exemple on comprend le lien avec : Combien puis je faire de groupes de 4 éléments avec 11 éléments disponibles ou encore dans 11 combien vont de fois 4.

Les personnes qui te disent "maîtriser" la division savent t'elles que cette opération n’existe pas en vrai. De façon personnel, je ne suis pas sur que pour comprendre une division on est obligé de passer par le corps des fractions d'un anneau et les relations d'équivalences .

La compréhension est toute relative. La finalité étant la maîtrise et la compréhension de la division, il faut à un moment maîtriser la technique. La compréhension peut venir en décalé cela ne parait pas un problème. De façon personnel, étant (très) bon techniquement je n'ai compris certains concepts que plusieurs années après avoir maîtrisé la technique ( et oui je suis long à la détente ).