Page 1 sur 2 • 1, 2 

 Marcel29Niveau 5
Marcel29Niveau 5
Bonjour,
A-t-on le droit d'écrire (racine(x))' pour parler de la dérivée de la fonction racine(x)?
Idem pour les autres expressions:
Exemple: f(x)=3*racine(x)+(4x-1)/(7x+3).
Peut-on écrire f'(x)=3*(racine(x))' + (4x-1)'(7x+3)-(4x-1)(7x+3)' / (7x+3)² ?
C'est tellement plus simple plutôt que de créer 36 000 fonctions u(x), v(x), w(x) etc... mais est-ce rigoureux? (Je l'ai vu dans pas mal de cours mais cela me semble peu rigoureux comme rédaction).
Merci!
A-t-on le droit d'écrire (racine(x))' pour parler de la dérivée de la fonction racine(x)?
Idem pour les autres expressions:
Exemple: f(x)=3*racine(x)+(4x-1)/(7x+3).
Peut-on écrire f'(x)=3*(racine(x))' + (4x-1)'(7x+3)-(4x-1)(7x+3)' / (7x+3)² ?
C'est tellement plus simple plutôt que de créer 36 000 fonctions u(x), v(x), w(x) etc... mais est-ce rigoureux? (Je l'ai vu dans pas mal de cours mais cela me semble peu rigoureux comme rédaction).
Merci!
 fifi51Fidèle du forum
fifi51Fidèle du forum
Je n'ai jamais vu cette notation, mais un prof de mathématiques saura mieux répondre.
Cette notation me choque un peu.
Intuitivement, je dirais qu'on dérive la fonction qui à x associe racine de x et non la racine.
Enfin, ce type de notation marcherait -t-il avec des fonctions de plusieurs variables ?
Cette notation me choque un peu.
Intuitivement, je dirais qu'on dérive la fonction qui à x associe racine de x et non la racine.
Enfin, ce type de notation marcherait -t-il avec des fonctions de plusieurs variables ?
_________________
Oui, j'ai un clavier Fisher Price pour l'instant !
 BrindIfFidèle du forum
BrindIfFidèle du forum
J'évite de le faire... Pourquoi ne pas introduire et utiliser la notation 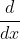 ?
?
 BrindIfFidèle du forum
BrindIfFidèle du forum
Cela permet de faire la différence entre 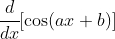 et
et 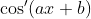
 BRNiveau 9
BRNiveau 9
 HélipsProphète
HélipsProphète
Je refuse que mes élèves le fasse. On ne dérive pas le nombre rac(x), ou alors ça fait 0.
Pour alléger le bazar, on peut les dispenser de poser toute la famille et d'appliquer juste soigneusement la formule. C'est ce que fait un de mes collègues, ça marche pas mal.
Pour alléger le bazar, on peut les dispenser de poser toute la famille et d'appliquer juste soigneusement la formule. C'est ce que fait un de mes collègues, ça marche pas mal.
_________________
Un jour, je serai prof, comme ça je serai toujours en vacances.
 Marcel29Niveau 5
Marcel29Niveau 5
Hélips a écrit:Je refuse que mes élèves le fasse. On ne dérive pas le nombre rac(x), ou alors ça fait 0.
Pour alléger le bazar, on peut les dispenser de poser toute la famille et d'appliquer juste soigneusement la formule. C'est ce que fait un de mes collègues, ça marche pas mal.
Aurais-tu un exemple précis car je ne vois pas bien.
Mon problème se situe dans le fait de vouloir être précis (pour ceux qui rament) sans alourdir avec "on prend u(x)=.... v(x)=... etc...".
Comment présenterais-tu la correction de l'exemple que j'ai mis dans mon premier post?
 HélipsProphète
HélipsProphète
Comme ça simplement :
f est la somme de la fonction racine et d'une fonction rationnelle, elle est donc dérivable sur son ensemble de définition privé de 0 soit ]0;+\infty[. Pour tout x>0 on a :

f est la somme de la fonction racine et d'une fonction rationnelle, elle est donc dérivable sur son ensemble de définition privé de 0 soit ]0;+\infty[. Pour tout x>0 on a :

_________________
Un jour, je serai prof, comme ça je serai toujours en vacances.
 JPhMMDemi-dieu
JPhMMDemi-dieu
Il faut distinguer la racine carrée d'un nombre et la fonction racine carrée, qui sont deux notions différentes.
Après, chacun est libre d'utiliser le symbole qu'il veut pour une fonction (dans la limite du raisonnable), alors pourquoi pas utiliser le symbole radical ? je n'y vois aucune faute de rigueur, mais seulement une faute de goût.
Mais alors la dérivée de √ s'écrirait √ '.
Sous ces notations, je pourrais alors accepter √ '(x).
Après, chacun est libre d'utiliser le symbole qu'il veut pour une fonction (dans la limite du raisonnable), alors pourquoi pas utiliser le symbole radical ? je n'y vois aucune faute de rigueur, mais seulement une faute de goût.
Mais alors la dérivée de √ s'écrirait √ '.
Sous ces notations, je pourrais alors accepter √ '(x).
_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
 HélipsProphète
HélipsProphète
Ah oui je suis d'accord. Même si je ne l'utilise pas, cette notation me paraît parfaitement correcte.
_________________
Un jour, je serai prof, comme ça je serai toujours en vacances.
 Marcel29Niveau 5
Marcel29Niveau 5
Ok merci pour ces précisions!
_________________
Il y a 3 sortes de mathématiciens, ceux qui savent compter et ceux qui ne savent pas compter.
 VinZTDoyen
VinZTDoyen
L'abus de notation du genre (cos x)' se rencontre parfois, y compris dans certains bouquins du supérieur. Si on peut, autant l'éviter (à une époque cela faisait hurler les IPR, maintenant, ils hurlent si on ne fait pas de TICE, autre temps, autres mœurs).
À l'inverse, prendre trois plombes pour poser u(x)=, v(x)= etc. ne me paraît pas très utile.
Pour dériver un produit du type f(x)=(x^2+1)(ln(x)+1), je fais reconnaître la forme (produit, quotient, faux-quotient, racine, etc.) puis j'écris la formule, mais sans les u, v:
f'(x)=( )( )+( )( )
puis ensuite je remplis les parenthèses. Cela ne fonctionne pas trop mal. Reste que le principal souci n'est pas là:
- les élèves connaissent de moins en moins bien les formules (ils les planquent dans la calculette, et du coup ne les apprennent pas)
- ils ont du mal à reconnaître un produit, un quotient, ... ! Il n'est pas rare d'entendre par exemple que f(x)=x*exp(x)+1 est un produit. Bref, toujours le même problème, les éléments de calcul algébrique, l'usage des parenthèse et le sens inhérent à ces calculs ne sont pas acquis pour un grand nombre.
À l'inverse, prendre trois plombes pour poser u(x)=, v(x)= etc. ne me paraît pas très utile.
Pour dériver un produit du type f(x)=(x^2+1)(ln(x)+1), je fais reconnaître la forme (produit, quotient, faux-quotient, racine, etc.) puis j'écris la formule, mais sans les u, v:
f'(x)=( )( )+( )( )
puis ensuite je remplis les parenthèses. Cela ne fonctionne pas trop mal. Reste que le principal souci n'est pas là:
- les élèves connaissent de moins en moins bien les formules (ils les planquent dans la calculette, et du coup ne les apprennent pas)
- ils ont du mal à reconnaître un produit, un quotient, ... ! Il n'est pas rare d'entendre par exemple que f(x)=x*exp(x)+1 est un produit. Bref, toujours le même problème, les éléments de calcul algébrique, l'usage des parenthèse et le sens inhérent à ces calculs ne sont pas acquis pour un grand nombre.
_________________
« Il ne faut pas croire tout ce qu'on voit sur Internet » Victor Hugo.
« Le con ne perd jamais son temps. Il perd celui des autres. » Frédéric Dard
« Ne jamais faire le jour même ce que tu peux faire faire le lendemain par quelqu'un d'autre » Pierre Dac
« Je n'ai jamais lâché prise !» Claude François
« Un économiste est un expert qui saura demain pourquoi ce qu'il avait prédit hier ne s'est pas produit aujourd'hui. » Laurence J. Peter
 JPhMMDemi-dieu
JPhMMDemi-dieu
Même certaines conventions d'écriture ne sont pas très correctes. Ainsi, le cos²(x), pour (cos(x))² , m'a toujours dérangé.
_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
 HélipsProphète
HélipsProphète
JPhMM a écrit:Même certaines conventions d'écriture ne sont pas très correctes. Ainsi, le cos²(x), pour (cos(x))² , m'a toujours dérangé.

_________________
Un jour, je serai prof, comme ça je serai toujours en vacances.
 M23Niveau 3
M23Niveau 3
JPhMM a écrit:Même certaines conventions d'écriture ne sont pas très correctes. Ainsi, le cos²(x), pour (cos(x))² , m'a toujours dérangé.
Ça me paraît pas vraiment une convention. Si f et g sont deux fonctions, f×g aussi. Dans le cas ou f=g, on note f², comme pour les réels, non?
Donc cos², c'est bien une fonction, définie justement par cos²(x) = (cos(x))².
Après, effectivement, il faut faire la différence entre f×f et fof…
 HélipsProphète
HélipsProphète
C'est pour ça que l'écrire sans préciser le sens de la notation comme on fait en lycée (moi y compris, hein) c'est moyen moyen.
_________________
Un jour, je serai prof, comme ça je serai toujours en vacances.
 leskhalNiveau 9
leskhalNiveau 9
(cos(x))' est très dérangeant à mon avis, même si certains profs le pratiquent, par contre
cos'(x) est correct.
Du coup, pour écrire (2x+1)', il faut poser, pour être correct, u(x)=2x+1...
C'est lourd, mais c'est le prix de l'exemplarité pour ne pas confondre fonction et expression d'une fonction.
Après chacun fait ce qu'il veut, les inspecteurs s'en foutent, chacun reste face à son éthique de notation...
cos'(x) est correct.
Du coup, pour écrire (2x+1)', il faut poser, pour être correct, u(x)=2x+1...
C'est lourd, mais c'est le prix de l'exemplarité pour ne pas confondre fonction et expression d'une fonction.
Après chacun fait ce qu'il veut, les inspecteurs s'en foutent, chacun reste face à son éthique de notation...
_________________
 Samuel DMNiveau 6
Samuel DMNiveau 6
Les puissances ça devient rigolo quand tu rajoutes la loi rond !
Pour ce qui est de la dérivée de racine de x avec des parenthèses, il m'arrive parfois de le faire lorsque ça évite des lourdeurs d'écritures en correction d'exercices. Lorsque je fais rédiger une correction, je contrains mes élèves à écrire un truc du genre: la fonction racine carrée, définie sur R+ et dérivable sur R+* admet pour dérivée x |-> 1/(2sqrt(x)) etc.
Je fais la chasse aux confusions "fonction f" et "réel f(x)" donc dans un tableau de variations, ils écrivent "signe de f'(x)" et "variations de f". Je zappe aussi les exercices dont l'énoncé commence par : soit f la fonction définie sur I par f(x)=...
En même temps, certains "anciens" profs confondent en notation f et f(x) tout en restant rigoureux pour le reste donc c'est difficile de trancher.
Pour ce qui est de la dérivée de racine de x avec des parenthèses, il m'arrive parfois de le faire lorsque ça évite des lourdeurs d'écritures en correction d'exercices. Lorsque je fais rédiger une correction, je contrains mes élèves à écrire un truc du genre: la fonction racine carrée, définie sur R+ et dérivable sur R+* admet pour dérivée x |-> 1/(2sqrt(x)) etc.
Je fais la chasse aux confusions "fonction f" et "réel f(x)" donc dans un tableau de variations, ils écrivent "signe de f'(x)" et "variations de f". Je zappe aussi les exercices dont l'énoncé commence par : soit f la fonction définie sur I par f(x)=...
En même temps, certains "anciens" profs confondent en notation f et f(x) tout en restant rigoureux pour le reste donc c'est difficile de trancher.
 BRNiveau 9
BRNiveau 9
Pour reprendre l'exemple cité, on peut écrire que f est dérivable sur son ensemble de définition car obtenue comme somme et quotient de fonctions dérivables. Comme :
=\underbrace{3\sqrt{x}}_{u(x)=3x^{\alpha}}+\underbrace{\frac{4x-1}{7x+3}}_{\frac{v(x)}{w(x)}})
nous en déduisons :
=\underbrace{3\times\frac{1}{2}x^{\frac{1}{2}-1}}_{u'(x)=3\alpha&space;x^{\alpha-1}}+\underbrace{\frac{1}{(7x+3)^{2}}\left(4\times&space;\bigl(7x+3\bigr)-\bigl(4x-1\bigr)\times&space;7&space;\right&space;)}_{\frac{1}{w^{2}(x)}\bigl(v'(x)w(x)-v(x)w'(x)&space;\bigr)})
Compte tenu du contexte, il n'y a guère d'ambiguïté quand à la définition des fonctions u, v et w et de la constante alpha.
Notez que je tiens à ce que mes élèves ne retiennent pas la dérivée de la fonction racine carrée, mais qu'ils la retrouvent à partir des dérivées des fonctions puissances.
nous en déduisons :
Compte tenu du contexte, il n'y a guère d'ambiguïté quand à la définition des fonctions u, v et w et de la constante alpha.
Notez que je tiens à ce que mes élèves ne retiennent pas la dérivée de la fonction racine carrée, mais qu'ils la retrouvent à partir des dérivées des fonctions puissances.
 VinZTDoyen
VinZTDoyen
BR a écrit:
Notez que je tiens à ce que mes élèves ne retiennent pas la dérivée de la fonction racine carrée, mais qu'ils la retrouvent à partir des dérivées des fonctions puissances.
Les puissances non entières ne sont plus au programme, cela dit ...
 HélipsProphète
HélipsProphète
VinZT a écrit:BR a écrit:
Notez que je tiens à ce que mes élèves ne retiennent pas la dérivée de la fonction racine carrée, mais qu'ils la retrouvent à partir des dérivées des fonctions puissances.
Les puissances non entières ne sont plus au programme, cela dit ...
C'est ce que j'allais dire : ça risque d'être compliqué en première
_________________
Un jour, je serai prof, comme ça je serai toujours en vacances.
 JPhMMDemi-dieu
JPhMMDemi-dieu
M23 a écrit:JPhMM a écrit:Même certaines conventions d'écriture ne sont pas très correctes. Ainsi, le cos²(x), pour (cos(x))² , m'a toujours dérangé.
Ça me paraît pas vraiment une convention. Si f et g sont deux fonctions, f×g aussi. Dans le cas ou f=g, on note f², comme pour les réels, non?
Donc cos², c'est bien une fonction, définie justement par cos²(x) = (cos(x))².
Après, effectivement, il faut faire la différence entre f×f et fof…
Oui, d'autant que f² désigne canoniquement une puissance fonctionnelle, non une puissance d'un nombre.Hélips a écrit:C'est pour ça que l'écrire sans préciser le sens de la notation comme on fait en lycée (moi y compris, hein) c'est moyen moyen.
_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
 JPhMMDemi-dieu
JPhMMDemi-dieu
Qui n'a pas utilisé x1/2 pour retenir la formule ?VinZT a écrit:BR a écrit:
Notez que je tiens à ce que mes élèves ne retiennent pas la dérivée de la fonction racine carrée, mais qu'ils la retrouvent à partir des dérivées des fonctions puissances.
Les puissances non entières ne sont plus au programme, cela dit ...
_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
 VinZTDoyen
VinZTDoyen
JPhMM a écrit:Qui n'a pas utilisé x1/2 pour retenir la formule ?VinZT a écrit:Les puissances non entières ne sont plus au programme, cela dit ...BR a écrit:
Notez que je tiens à ce que mes élèves ne retiennent pas la dérivée de la fonction racine carrée, mais qu'ils la retrouvent à partir des dérivées des fonctions puissances.
Au stade algébrique où en sont nos élèves, j'aime autant qu'ils apprennent la dérivée de racine(x). Les puissances fractionnaires, qui deviennent négatives en dérivant, deux bonnes raisons de
 HélipsProphète
HélipsProphète
+1 !
_________________
Un jour, je serai prof, comme ça je serai toujours en vacances.
Page 1 sur 2 • 1, 2 

- Détermination d'un volumé équivalent lors d'un dosage potentiométrique par méthode de la dérivée première ou de la dérivée seconde
- question de notation de dérivée.
- [Mathématiques] limite et dérivée (1eS)
- Enseignement privé au Québec : la concurrence est rude entre écoles et entre élèves.
- Preview sur la rigueur ? Les profs d'EPS à 26 heures ?
Permission de ce forum:
Vous ne pouvez pas répondre aux sujets dans ce forum



