Page 3 sur 4 •  1, 2, 3, 4
1, 2, 3, 4 
 1, 2, 3, 4
1, 2, 3, 4 
- AdriGrand Maître
ouais, ben mon fils est en cm1, il adore les maths aussi, mais en classe, ils sont loiiiin de la fraction : ils abordent à peine la division 
Pas étonnant qu'il s'ennuie en classe...

Pas étonnant qu'il s'ennuie en classe...
 RuthvenGuide spirituel
RuthvenGuide spirituel
V.Marchais a écrit:Alors, si on commence à partir dans les techniques visuelles, ça va être tout un poème.
Fiston a une manière bien à lui de compter, très "visuelle", justement. J'ai pas tout compris à ce jour. Il associe les chiffres à des formes (3 = triangle, 4 = carré) et il compte comme ça. Par exemple, sur les cartes (de jeu), ça se "voit", dit-il : 7 = 5 + 2 (le carré du cinq avec son point au milieu + les deux points en haut) ou 5 = 4 + 3 (le carré + le triangle. Tu suis ?) Pour les multiplications, il fait des trucs pareils que j'ai du mal à suivre (j'ai du mal à me représenter ce qu'il visualise et comment il le manipule) mais c'est efficace : il calcule rapidement. Et, crois-le si tu peux, quand nous avons discuté des puissances, suite à une émission qu'il avait vue à la télé, c'est lui qui m'a fait remarquer que c'était logique que les puissances deux s'appellent des "carrés" parce que 4x4 ça dessine un carré (jusque là, encore, oui, d'accord) et que celles de trois s'appellent des "cubes", parce que ça dessinait des cubes : trois puissance trois, ça fait un cube de trois points de côté, qui contient en tout 27 points et 4 puissance 4 ça fait 4 carrés de 16 points empilés... Certes...
:study:
Je ne sais pas s'il y a beaucoup d'enfants qui raisonnent comme ça, mais moi, je m'y perds. A côté, les tables, qu'est-ce que c'est confortable, finalement...
Et avec tout ça, Toto est pas foutu de voir qu'il suffisait de prendre des moitiés de colonnes au lieu des colonnes pour faire son exercice ! Ah mais j'vous jure !
Il est pythagoricien ! Cf. l'histoire des nombres triangle et des nombres carré.
 V.MarchaisEmpereur
V.MarchaisEmpereur
Alors là, c'est la meilleure ! :lol:
Véronique, morte de rire.
Véronique, morte de rire.
 V.MarchaisEmpereur
V.MarchaisEmpereur
Adri a écrit:ouais, ben mon fils est en cm1, il adore les maths aussi, mais en classe, ils sont loiiiin de la fraction : ils abordent à peine la division
Pas étonnant qu'il s'ennuie en classe...
S'il s'ennuie et qu'il a envie de découvrir, tu peux peut-être commencer avec lui certains trucs, sous forme de jeux ?
 AdriGrand Maître
AdriGrand Maître
oh oui, on a fait quelques trucs - en math, surtout son père -
La méthode de calcul de ton fiston me laisse sans voix... et me fait penser à une émission où j'avais entendu que certains mathématiciens avaient un rapport tout personnel aux nombres qu'ils associaient à des couleurs par exemple...
La méthode de calcul de ton fiston me laisse sans voix... et me fait penser à une émission où j'avais entendu que certains mathématiciens avaient un rapport tout personnel aux nombres qu'ils associaient à des couleurs par exemple...
 RuthvenGuide spirituel
RuthvenGuide spirituel
V.Marchais a écrit:Alors là, c'est la meilleure ! :lol:
Véronique, morte de rire.
Regarde ici sur le lien entre nombre et figure dans le pythagorisme :
http://www.clevislauzon.qc.ca/professeurs/mathematiques/rossa/Logimath%5CPythagA.pps
http://accromath.uqam.ca/contents/pdf/Pythagore.pdf
http://newton.mat.ulaval.ca/amq/bulletins/oct06/Nombrespolygonaux.pdf
JPhhM doit avoir des liens sur la question.
 V.MarchaisEmpereur
V.MarchaisEmpereur
Adri a écrit:oh oui, on a fait quelques trucs - en math, surtout son père -
La méthode de calcul de ton fiston me laisse sans voix... et me fait penser à une émission où j'avais entendu que certains mathématiciens avaient un rapport tout personnel aux nombres qu'ils associaient à des couleurs par exemple...
Alors là, la couleur, c'est encore plus mystique que les formes. J'arrive encore à voir le lien entre nombres et formes et, pour certains calculs, à voir comment Doudou raisonne, mais entre nombres et couleurs... Vert + bleu = ???

On va les mettre ensemble, ils vont peut-être fonder une nouvelle secte qui fera de brillants émules. :lol:
 V.MarchaisEmpereur
V.MarchaisEmpereur
Ruthven a écrit:V.Marchais a écrit:Alors là, c'est la meilleure ! :lol:
Véronique, morte de rire.
Regarde ici sur le lien entre nombre et figure dans le pythagorisme :
http://www.clevislauzon.qc.ca/professeurs/mathematiques/rossa/Logimath%5CPythagA.pps
http://accromath.uqam.ca/contents/pdf/Pythagore.pdf
http://newton.mat.ulaval.ca/amq/bulletins/oct06/Nombrespolygonaux.pdf
JPhhM doit avoir des liens sur la question.
Merci Ruthven, c'est super intéressant.
Je ne connaissais pas tout ça.
Mais blague à part, en restant dans les "nombres triangulaires", alors, je crois bien que c'est quelque chose comme ça, qu'il fait, mon grand. En tout cas, pour les carrés et les cubes, c'est évident. Il est vraiment pythagoricien, c'était même pas une blague ! :shock:
Bon, ben, je vous préviendrai quand il en sera aux nombres pentagonaux...
 JPhMMDemi-dieu
JPhMMDemi-dieu
Ruthven a écrit:V.Marchais a écrit:Alors, si on commence à partir dans les techniques visuelles, ça va être tout un poème.
Fiston a une manière bien à lui de compter, très "visuelle", justement. J'ai pas tout compris à ce jour. Il associe les chiffres à des formes (3 = triangle, 4 = carré) et il compte comme ça. Par exemple, sur les cartes (de jeu), ça se "voit", dit-il : 7 = 5 + 2 (le carré du cinq avec son point au milieu + les deux points en haut) ou 5 = 4 + 3 (le carré + le triangle. Tu suis ?) Pour les multiplications, il fait des trucs pareils que j'ai du mal à suivre (j'ai du mal à me représenter ce qu'il visualise et comment il le manipule) mais c'est efficace : il calcule rapidement. Et, crois-le si tu peux, quand nous avons discuté des puissances, suite à une émission qu'il avait vue à la télé, c'est lui qui m'a fait remarquer que c'était logique que les puissances deux s'appellent des "carrés" parce que 4x4 ça dessine un carré (jusque là, encore, oui, d'accord) et que celles de trois s'appellent des "cubes", parce que ça dessinait des cubes : trois puissance trois, ça fait un cube de trois points de côté, qui contient en tout 27 points et 4 puissance 4 ça fait 4 carrés de 16 points empilés... Certes...
:study:
Je ne sais pas s'il y a beaucoup d'enfants qui raisonnent comme ça, mais moi, je m'y perds. A côté, les tables, qu'est-ce que c'est confortable, finalement...
Et avec tout ça, Toto est pas foutu de voir qu'il suffisait de prendre des moitiés de colonnes au lieu des colonnes pour faire son exercice ! Ah mais j'vous jure !
Il est pythagoricien ! Cf. l'histoire des nombres triangle et des nombres carré.
Oui, c'est exactement ça.
L'être humain (sous-entendu "sans capacité exceptionnelle") "voyant instinctivement" jusqu'à quatre (s'il y a trois allumettes par terre, je sais qu'elles sont 3. S'il y en a quatre, je sais qu'elles sont quatre. S'il y en a cinq, il me faut déclencher une méthode de "séparation" allumettes pour identifier qu'elles sont cinq.), il utilise cette capacité naturelle. Il associe chaque nombre à un motif géométrique (en général, jusqu'à carré instinctivement, ensuite il faut procéder à des séparations). Et en opérant sur les motifs, il réalise des applications qu'on appelle isomorphismes pour faire du calcul.
nombres a et b => motifs A et B => opération sur A et B => motif C => nombre c (par comptage ou association)
Et par isomorphisme, l'opération sur a et b = c
Ça marche très bien avec des nombres entiers positifs.
Avec des nombres décimaux, ça deviendra plus compliqué. Comment calculer 2,5² avec cette méthode ? (en collège)
L'avantage des écritures fractionnaires, c'est que c'est transposable, puisqu'une fraction est le rapport de deux nombres entiers.
En effet : 2,5² = (5/2)² = 25/4 = (24,0+1,0)/4 = (12+0,5)/2 = 12,50/2 = 6,25. Certains collégiens savent faire cela de tête, même s'ils sont rares. Les autres trouvent cela absolument mystérieux.
J'avoue que le coup de voir 4 puissance 4 comme un hypercube de dimension 4, de 4 points x 4 points x 4 points x 4 points est assez bluffant de sa part.

Edit : erreur de frappe.
_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
 V.MarchaisEmpereur
V.MarchaisEmpereur
Euh... c'est quoi un hypercube ?
Faut que je demande à mon fils ?
Faut que je demande à mon fils ?
 JPhMMDemi-dieu
JPhMMDemi-dieu
V.Marchais a écrit:Ruthven a écrit:V.Marchais a écrit:Alors là, c'est la meilleure ! :lol:
Véronique, morte de rire.
Regarde ici sur le lien entre nombre et figure dans le pythagorisme :
http://www.clevislauzon.qc.ca/professeurs/mathematiques/rossa/Logimath%5CPythagA.pps
http://accromath.uqam.ca/contents/pdf/Pythagore.pdf
http://newton.mat.ulaval.ca/amq/bulletins/oct06/Nombrespolygonaux.pdf
JPhhM doit avoir des liens sur la question.
Merci Ruthven, c'est super intéressant.
Je ne connaissais pas tout ça.
Mais blague à part, en restant dans les "nombres triangulaires", alors, je crois bien que c'est quelque chose comme ça, qu'il fait, mon grand. En tout cas, pour les carrés et les cubes, c'est évident. Il est vraiment pythagoricien, c'était même pas une blague ! :shock:
Bon, ben, je vous préviendrai quand il en sera aux nombres pentagonaux...
La qualité de ces méthodes vient du fait qu'elles sont extrêmement élégantes, c'est-à-dire esthétiquement remarquables.
Par exemple :

comme Pythagore, je trouve somptueux le fait que 1+2+3+4 = 10.
C'est simplissime, mais c'est d'une beauté à couper le souffle.
_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
 JPhMMDemi-dieu
JPhMMDemi-dieu

Hypercube ? il faut de l'imagination.
Tu as un segment (une dimension), tu "tires" dessus (imagine qu'il soit "élastique" et que tu peux l'étendre sur une surface), ça fait un carré (2 dimensions)
Tu tires sur un carré, ça fait un cube (3 dimensions)
Tu tires sur le cube, ça fait un hypercube de dimension 4.
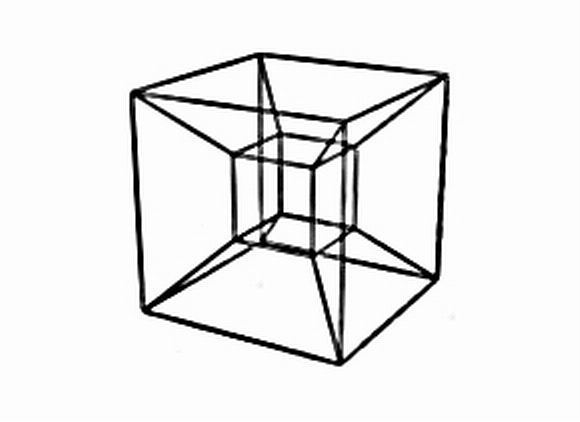
Représentation classique d'hypercube :
_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
 V.MarchaisEmpereur
V.MarchaisEmpereur
Oui, moi aussi, je trouve ça un peu magique.
Cette "suite", je la connais, tout de même, ainsi que la fameuse "corde à 12 noeuds de Pythagore" dont se seraient servi les architectes médiévaux (attesté ?) : 3² + 4² = 5²
J'ai choisi la poésie, mais j'ai adoré les maths et je crois que je trouvais dans les équations le même sentiment d'harmonie, de limpidité soudaine du monde qui devient intelligible. C'est comme la poésie, en fait : que de l'illusion, du signe - mais qu'est-ce que ça fait du bien.
En tout cas, ça me fait plaisir que Doudou aime les chiffres aussi - et manifestement, on va pouvoir s'en donner à coeur joie. C'est moi qui vais vite être en reste. J'ai tellement oublié...
Cette "suite", je la connais, tout de même, ainsi que la fameuse "corde à 12 noeuds de Pythagore" dont se seraient servi les architectes médiévaux (attesté ?) : 3² + 4² = 5²
J'ai choisi la poésie, mais j'ai adoré les maths et je crois que je trouvais dans les équations le même sentiment d'harmonie, de limpidité soudaine du monde qui devient intelligible. C'est comme la poésie, en fait : que de l'illusion, du signe - mais qu'est-ce que ça fait du bien.
En tout cas, ça me fait plaisir que Doudou aime les chiffres aussi - et manifestement, on va pouvoir s'en donner à coeur joie. C'est moi qui vais vite être en reste. J'ai tellement oublié...
 JPhMMDemi-dieu
JPhMMDemi-dieu
Calculons le nombre de "sommets" :
Segment : 2 extrémités (= 2 puissance 1, 1 étant le nombre de dimensions du segment)
Carré : 4 sommets (= 2 puissance 2, 2 étant le nombre de dimensions du carré)
Cube : 8 sommets (= 2 puissance 3, 3 étant le nombre de dimensions du cube)
4-Hypercube : 16 sommets (= 2 puissance 4, 4 étant le nombre de dimensions de l'hypercube de dimension 4, aussi appelé 4-hypercube)
Il suffit de compter le nombre de sommets
Segment : 2 extrémités (= 2 puissance 1, 1 étant le nombre de dimensions du segment)
Carré : 4 sommets (= 2 puissance 2, 2 étant le nombre de dimensions du carré)
Cube : 8 sommets (= 2 puissance 3, 3 étant le nombre de dimensions du cube)
4-Hypercube : 16 sommets (= 2 puissance 4, 4 étant le nombre de dimensions de l'hypercube de dimension 4, aussi appelé 4-hypercube)
Il suffit de compter le nombre de sommets
_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
 V.MarchaisEmpereur
V.MarchaisEmpereur
JPhMM a écrit:
Hypercube ? il faut de l'imagination.
Tu as un segment (une dimension), tu "tires" dessus (imagine qu'il soit "élastique" et que tu peux l'étendre sur une surface), ça fait un carré (2 dimensions)
Tu tires sur un carré, ça fait un cube (3 dimensions)
Tu tires sur le cube, ça fait un hypercube de dimension 4.
Représentation classique d'hypercube :
Ca y est, je suis larguée ! :lol:
Je veux bien, moi, tirer sur le cube - mais dans quelle direction ?

Je ne peux pas te garantir que c'est ça qu'il voit, Fiston. J'avoue que, là, ça me dépasse.
 V.MarchaisEmpereur
V.MarchaisEmpereur
JPhMM a écrit:Calculons le nombre de "sommets" :
Segment : 2 extrémités (= 2 puissance 1, 1 étant le nombre de dimensions du segment)
Carré : 4 sommets (= 2 puissance 2, 2 étant le nombre de dimensions du carré)
Cube : 8 sommets (= 2 puissance 3, 3 étant le nombre de dimensions du cube)
4-Hypercube : 16 sommets (= 2 puissance 4, 4 étant le nombre de dimensions de l'hypercube de dimension 4, aussi appelé 4-hypercube)
Il suffit de compter le nombre de sommets
Ah ! Merci, ça va mieux. On revient aux chiffres, à l'abstraction : ouf !
C'est confirmé : je ne suis pas une visuelle.
 V.MarchaisEmpereur
V.MarchaisEmpereur
Ah ouaiiiiiiiiiiiiiiis !  Avec l'explication théorique, j'ai même réussi à les compter sur la figure que je trouvais illisible, les sommets.
Avec l'explication théorique, j'ai même réussi à les compter sur la figure que je trouvais illisible, les sommets.
Qu'est-ce que je me sens futée, tout de suite !
 Avec l'explication théorique, j'ai même réussi à les compter sur la figure que je trouvais illisible, les sommets.
Avec l'explication théorique, j'ai même réussi à les compter sur la figure que je trouvais illisible, les sommets.Qu'est-ce que je me sens futée, tout de suite !
 JPhMMDemi-dieu
JPhMMDemi-dieu
V.Marchais a écrit:Ca y est, je suis larguée ! :lol:
Je veux bien, moi, tirer sur le cube - mais dans quelle direction ?
Je ne peux pas te garantir que c'est ça qu'il voit, Fiston. J'avoue que, là, ça me dépasse.
Dans quelle direction ? mais dans la quatrième, bien sûr !!!
Le problème, en effet, c'est que nous ne voyons que trois dimensions spatiales.
Contournons la difficulté.
La seule quatrième dimension qui nous soit naturelle est le temps.
Imagine que ton cube rétrécit.
Au début il est "grand" et avec le temps il devint "petit".
Superpose tous les instants de ce rétrécissement, et tu obtiens la représentation que je t'ai donnée.
Mais ce n'est qu'une représentation...
_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
 V.MarchaisEmpereur
V.MarchaisEmpereur
A y est, j'ai pigé.
Toi, tu devrais faire prof de maths... :lol:
Toi, tu devrais faire prof de maths... :lol:
 V.MarchaisEmpereur
V.MarchaisEmpereur
JPhMM a écrit:
Dans quelle direction ? mais dans la quatrième, bien sûr !!!

 JPhMMDemi-dieu
JPhMMDemi-dieu
Bien sûr, faire ça est cognitivement peu économique.
Avec l'expérience, on comprend que pour passer du segment au carré, on dédouble le segment (un en bas, un en haut) et on relie les extrémités dédoublées.
Pour faire un cube, on dédouble le carré, etc...
Et tu comprends pourquoi il dédouble le cube pour calculer à la puissance 4, puisque pour obtenir le 4-hypercube, on dédouble le cube, etc...
Et là, on a gagné en économie. Au lieu de devoir se représenter la chose, on applique une opération, le dédoublement de la figure initiale (qui est loin d'être aussi simple qu'on le pense... essayer de faire ça avec un "segment de 4 points" est une autre paire de manches...)
Avec l'expérience, on comprend que pour passer du segment au carré, on dédouble le segment (un en bas, un en haut) et on relie les extrémités dédoublées.
Pour faire un cube, on dédouble le carré, etc...
Et tu comprends pourquoi il dédouble le cube pour calculer à la puissance 4, puisque pour obtenir le 4-hypercube, on dédouble le cube, etc...
Et là, on a gagné en économie. Au lieu de devoir se représenter la chose, on applique une opération, le dédoublement de la figure initiale (qui est loin d'être aussi simple qu'on le pense... essayer de faire ça avec un "segment de 4 points" est une autre paire de manches...)
_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
 JPhMMDemi-dieu
JPhMMDemi-dieu
Je ne pense pas qu'il voit l'hypercube en représentation "canonique", mais il comprend que pour 4 puissance 4, il faut faire 4 tranches qui sont chacune un cube 4 puissance 3. Il a donc sa façon à lui de le voir.V.Marchais a écrit:Je ne peux pas te garantir que c'est ça qu'il voit, Fiston. J'avoue que, là, ça me dépasse.
_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
 doctor whoDoyen
doctor whoDoyen
Ca me fait penser au roman Flatland, où un carré découvre grâce à l'apprition d'une sphère la trosième dimension, et est bien emmerdé pour dire dans quelle direction il faut tirer un carré pour faire un cube.
Chapitre 9 - Comment je voulus enseigner la théorie des Trois Dimensions à mon petit-fils, et avec quel succès
Je me réveillai heureux et je réfléchis à la glorieuse carrière qui m'attendait. Je me dis que j'allais immédiatement me mettre en marche pour évangéliser tout Flatland. L'Évangile des Trois Dimensions serait proclamé même aux Femmes et aux Soldats. Je commencerais par mon Épouse
Je venais à peine de décider le plan de mes opérations lorsque j'entendis dans la rue plusieurs voix qui réclamaient le silence. Une autre s'éleva, plus forte. C'était une proclamation du héraut. J'écoutai attentivement et je reconnus la Résolution du Conseil, qui décrétait l'arrestation, l'emprisonnement ou la détention de tous ceux qui pervertiraient l'esprit du peuple par des illusions et déclareraient avoir reçu des révélations d'un autre Monde.
Je m'abîmai dans mes pensées. Ce danger n'était pas à négliger. Mieux vaudrait éviter de faire allusion à ma Révélation et m'engager sur la voie de la Démonstration – celle-ci étant, somme toute, si simple et si concluante que, si j'omettais la première méthode, la vérité n'y perdrait rien. – « Vers le Haut, et non vers le Nord » telle était la clef de toute l'affaire. J'avais trouvé celle-ci assez claire avant de m'endormir au réveil, alors que mon esprit émergeait à peine du rêve, elle me paraissait aussi évidente que l'Arithmétique elle-même mais, je ne savais pourquoi, l'explication ne me semblait plus à présent s'imposer vraiment d'elle-même. Malgré l'entrée opportune de ma Femme, qui pénétra dans ma chambre à ce moment-là, je décidai, après avoir échangé avec elle quelques mots anodins, de ne pas commencer par elle.
Mes Fils Pentagonaux, personnes respectables et médecins d'excellente réputation, ne valaient cependant rien en mathématiques et ne pouvaient donc pas m'être d'une utilité quelconque à cet égard. Mais il me vint à l'esprit qu'un Hexagone jeune et docile, ayant l'esprit mathématique, ferait un fort bon élève. Dans ces conditions, pourquoi ne pas tenter l'expérience avec mon précoce Petit-fils dont les remarques accidentelles avaient suscité l'approbation de la Sphère ? Comme ce n'était qu'un enfant, je ne risquerais rien en discutant de cette question avec lui, car il n'aurait pas connaissance de la Proclamation du Conseil alors qu'avec mes Fils – dont le patriotisme et la déférence vis-à-vis des Cercles l'emportaient de beaucoup sur les élans aveugles de l'affection – rien ne m'assurait qu'ils ne se sentiraient pas contraints de me dénoncer au Préfet s'ils jugeaient que je soutenais fermement l'hérésie séditieuse de la Troisième Dimension.
Mais il fallait avant tout trouver un moyen de satisfaire la curiosité de ma Femme, qui désirait naturellement savoir pourquoi le Cercle avait souhaité cet entretien mystérieux et comment il avait pénétré dans la maison. Sans entrer dans tous les détails du récit compliqué que je lui fis – récit qui n'était pas, je le crains, aussi conforme à la vérité que l'aimeraient mes Lecteurs de Spaceland – je me contenterai de dire que je parvins à la persuader de se remettre à ses travaux domestiques sans avoir mentionné une seule fois le Monde des Trois Dimensions. Cela étant fait, j'envoyai immédiatement chercher mon Petit-fils car, pour tout avouer, je sentais ce que j'avais vu et entendu m'échapper d'une façon étrange, telle l'image à demi saisie d'un songe qui vous tourmente, et je désirais mettre mon habileté à l'épreuve en me faisant un premier disciple.
Dès que mon Petit-Fils fut entré dans la pièce, je cadenassai soigneusement la porte. Puis nous nous assîmes côte à côte et, prenant nos tablettes mathématiques – ou nos Lignes, diriez-vous – je déclarai que nous allions reprendre la leçon de la veille. Je lui répétai qu'un Point, lorsqu'il se meut en une Dimension, produit une Ligne, et qu'une Ligne Droite produit un Carré en Deux Dimensions. Après quoi, en me forçant à rire, je lui dis : « Et maintenant, petit garnement, vous vouliez me faire croire qu'un Carré, en se déplaçant selon la même méthode, mais « vers le Haut et non pas vers le Nord », produit une autre figure, une sorte d'Extra-Carré en Trois Dimensions. Redites-moi cela, jeune brigand. »
À cet instant même, nous entendîmes de nouveau, dans la rue, le « Oyez, oyez » du héraut, qui proclamait la Résolution du Conseil. Aussi jeune qu'il fût, mon Petit-fils – qui était d'une intelligence inhabituelle pour son âge, et élevé dans le respect total de l'autorité des Cercles – saisit la situation avec une rapidité à laquelle je ne m'attendais pas. Il resta silencieux pendant que la voix du héraut s'éloignait, puis, éclatant en sanglots : « Cher Grand-papa », me dit-il, « je voulais seulement plaisanter et je ne pensais, bien sûr, à rien de sérieux et nous n'étions pas, à ce moment-là, au courant de la nouvelle Loi et je ne crois pas vous avoir dit quoi que ce soit de la Troisième Dimension et je suis certain de ne pas avoir prononcé les mots « Vers le Haut et non pas vers le Nord », car ce serait stupide, vous le savez bien. Comment un objet pourrait-il se mouvoir vers le Haut et non pas vers le Nord ? Vers le Haut et non pas vers le Nord ! Même si j'étais encore bébé, je ne serais pas aussi sot. Que c'est bête ! Ah ! ah ! ah ! »
« Ce n'est pas si bête », dis-je, agacé. « Tenez, par exemple, je prends ce Carré » – et sur ces mots je m'emparai d'un Carré mobile qui était posé là – « et je le déplace, comme vous voyez, non pas vers le Nord mais – oui, je le déplace vers le Haut – c'est-à-dire, non pas vers le Nord… en fait, je le transporte quelque part… pas ainsi, mais d'une façon… » Mon explication déboucha sur le vide et je secouai le Carré de tous côtés, au grand amusement de mon Petit-fils, qui se mit à rire de plus en plus belle et déclara que je jouais avec lui au lieu de l'instruire ce faisant il ouvrit la porte et quitta la pièce en courant. Ainsi s'acheva la première tentative que je fis pour convertir un élève à l'Évangile des Trois Dimensions.
_________________
Mon blog sur Tintin (entre autres) : http://popanalyse.over-blog.com/
Blog pédagogique : http://pedagoj.eklablog.com
 JPhMMDemi-dieu
JPhMMDemi-dieu
Exactement.
Le monde des créatures de dimension 2 qui essaient de comprendre la dimension 3 :
http://dimensions.umpa.ens-lyon.fr/fichiers/DIMENSIONS_I/Chap2_francais.mov
Et nous autres, en dimension 3, essayons de comprendre la dimension 4 :
http://dimensions.umpa.ens-lyon.fr/fichiers/DIMENSIONS_I/Chap3_francais.mov
A voir, ne serait-ce que parce que c'est beau.
Edit : faute de frappe.
Le monde des créatures de dimension 2 qui essaient de comprendre la dimension 3 :
http://dimensions.umpa.ens-lyon.fr/fichiers/DIMENSIONS_I/Chap2_francais.mov
Et nous autres, en dimension 3, essayons de comprendre la dimension 4 :
http://dimensions.umpa.ens-lyon.fr/fichiers/DIMENSIONS_I/Chap3_francais.mov
A voir, ne serait-ce que parce que c'est beau.
Edit : faute de frappe.
_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
 V.MarchaisEmpereur
V.MarchaisEmpereur
Moi, j'avais lu ça dans une très belle BD, L'Origine. Quelqu'un connaît ?
 JPhMMDemi-dieu
JPhMMDemi-dieu
Je ne connaissais pas.
Merci pour l'information
Merci pour l'information
_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
Page 3 sur 4 •  1, 2, 3, 4
1, 2, 3, 4 
 1, 2, 3, 4
1, 2, 3, 4 
Permission de ce forum:
Vous ne pouvez pas répondre aux sujets dans ce forum


