Page 1 sur 4 • 1, 2, 3, 4 

 V.MarchaisEmpereur
V.MarchaisEmpereur
Demande particulière aux collègues profs de math et instits.
J'ai un fils en CM1 qui adore les maths, si, si, je vous jure. Jusque là, aucun problème : les problèmes, justement, sont un jeu, les opérations, c'est fastoche... Il fait sans problème multiplications et divisions de nombres entiers...
Mais là, nous nous heurtons à un os. Fiston a appris les fractions. Il a des exercices à faire de réduction de fractions (j'espère que j'emploie les bons termes, je veux dire : des exercices du style 4/16 = 1/4 etc.). Et là, il patauge complètement. Il y a manifestement un truc qui lui a échappé : tout ce qu'il pose est faux. Personnellement, je n'ai pu que lui donner la méthode que j'ai moi-même apprise : on décompose le numérateur et le dénominateur en nombres premiers et on divise par tous les éléments communs. Mais voilà, "La maîtresse, elle dit de pas faire comme ça". Argh. Et comment donc ? La feuille d'exercices est couverte de tableaux quadrillés dont certaines cases contiguës sont grisées et il faudrait se servir de ces tableaux pour réduire les fractions. Comment ? Mystère. Ces cases ne dessinent pas des formes assez régulières pour qu'on puisse déduire à vue d'oeil que tel rapport fait en fait un quart ou un septième. Et puis je me demande bien quel serait l'intérêt.
Je veux bien essayer d'entrer dans cette démarche pour la réexpliquer à Junior - encore faudrait-il que je la comprisse moi-même. Pour l'instant, je lui demande de faire la méthode "classique", en décomposant les nombres, il a compris, mais il rechigne en grognant : "C'est pas ça qu'y faut faire."

Quoi, alors ? Comment enseigne-t-on les fractions en primaire, désormais ? C'est quoi, ce bordel ? Déjà que je dois refaire la moitié des leçons de grammaire (bon, ça, au moins, je sais faire), si je dois refaire les maths en plus, on n'est pas rendus...
Que puis-je faire pour l'aider, mon Toto ?
J'ai un fils en CM1 qui adore les maths, si, si, je vous jure. Jusque là, aucun problème : les problèmes, justement, sont un jeu, les opérations, c'est fastoche... Il fait sans problème multiplications et divisions de nombres entiers...
Mais là, nous nous heurtons à un os. Fiston a appris les fractions. Il a des exercices à faire de réduction de fractions (j'espère que j'emploie les bons termes, je veux dire : des exercices du style 4/16 = 1/4 etc.). Et là, il patauge complètement. Il y a manifestement un truc qui lui a échappé : tout ce qu'il pose est faux. Personnellement, je n'ai pu que lui donner la méthode que j'ai moi-même apprise : on décompose le numérateur et le dénominateur en nombres premiers et on divise par tous les éléments communs. Mais voilà, "La maîtresse, elle dit de pas faire comme ça". Argh. Et comment donc ? La feuille d'exercices est couverte de tableaux quadrillés dont certaines cases contiguës sont grisées et il faudrait se servir de ces tableaux pour réduire les fractions. Comment ? Mystère. Ces cases ne dessinent pas des formes assez régulières pour qu'on puisse déduire à vue d'oeil que tel rapport fait en fait un quart ou un septième. Et puis je me demande bien quel serait l'intérêt.
Je veux bien essayer d'entrer dans cette démarche pour la réexpliquer à Junior - encore faudrait-il que je la comprisse moi-même. Pour l'instant, je lui demande de faire la méthode "classique", en décomposant les nombres, il a compris, mais il rechigne en grognant : "C'est pas ça qu'y faut faire."

Quoi, alors ? Comment enseigne-t-on les fractions en primaire, désormais ? C'est quoi, ce bordel ? Déjà que je dois refaire la moitié des leçons de grammaire (bon, ça, au moins, je sais faire), si je dois refaire les maths en plus, on n'est pas rendus...
Que puis-je faire pour l'aider, mon Toto ?
 frimoussette77Guide spirituel
frimoussette77Guide spirituel
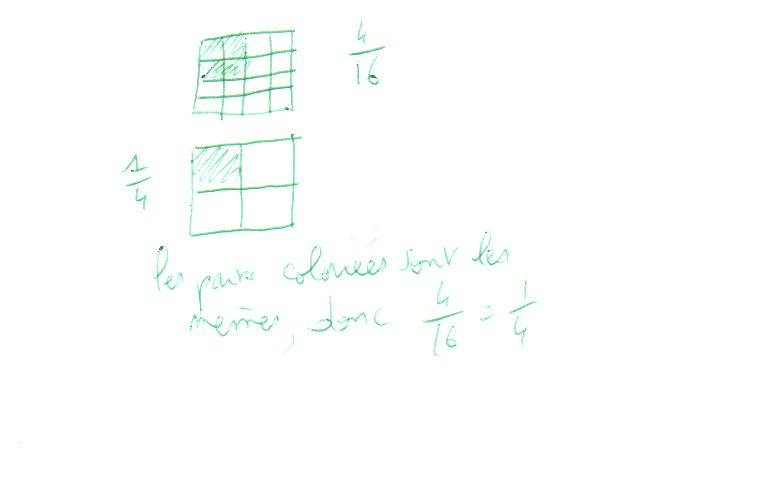
Mon mari a dessiné un petit croquis pas très joli mais qui explique le phénomène, vois-tu ce qu'il veut dire ?
 InvitéInvité
InvitéInvité
J'avais déjà vu ce type de dessin. C'est très pratique pour des fractions comme 1/4 mais je trouve que ça se complique pour des fractions à dénominateur impair, à cause de la forme géométrique obtenue en coloriant. Et j'ai l'impression que le choix de la découpe en carrés (le nombre et la disposition) n'est pas dû au hasard... mais suppose de connaître déjà les diviseurs du numérateur de la fraction à simplifier. Un prof de maths pour nous expliquer tout ça?
 V.MarchaisEmpereur
V.MarchaisEmpereur
Al a écrit:J'avais déjà vu ce type de dessin. C'est très pratique pour des fractions comme 1/4 mais je trouve que ça se complique pour des fractions à dénominateur impair, à cause de la forme géométrique obtenue en coloriant.
C'est bien ça le problème. J'essaierai de prendre le temps de scanner la feuille d'exos de Junior, cet aprèm. Quand on a, sur le quadrillage, non plus 1/4 bien localisé mais une colonne et quelques carreaux de l'autre colonne grisés, il n'y a plus rien de visible, justement. Je ne vois pas comment on peut appliquer ce système avec des nombres un peu complexes.

 V.MarchaisEmpereur
V.MarchaisEmpereur
Frimousette, merci à toi et ton mari. Jusque là, je comprends, mais quand c'est plus complexe, comme rapport ?
Il faut vraiment que je vous scanne la feuille.
Il faut vraiment que je vous scanne la feuille.
 Pierre_au_carréGuide spirituel
Pierre_au_carréGuide spirituel
V.Marchais a écrit:Frimousette, merci à toi et ton mari. Jusque là, je comprends, mais quand c'est plus complexe, comme rapport ?
Il faut vraiment que je vous scanne la feuille.
Il attend la 6ième ou la 5ième...

Dans ce que tu décris, peut-être qu'il faut imaginer les dimensions du rectangle.
 frimoussette77Guide spirituel
frimoussette77Guide spirituel
Mais on ne peut faire que des partages pairs.Provence a écrit:Essaie avec un gâteau: "Préfères-tu 2/8 ou 1/4"?
 V.MarchaisEmpereur
V.MarchaisEmpereur
Je crois qu'il a compris le principe des fractions. En classe, les élèves ont manipulé des rapports variés : parts de "camemberts" (ou de gâteau si tu préfères - moi, je suis plutôt un bec salé :lol: ), cases d'une grille ou d'un tableau. C'est bien, c'est assez éloquent, je crois, pour montrer qu'on parle bien d'un rapport.
Là où ça se complique, c'est pour les équivalences, ou réductions de fraction.
L'exercice consiste en une série de tableaux de 10 cases par 10 cases, soit cent au total, dont une partie est grisée, partie qu'il faut traduire sous forme de fraction, d'abord sur 100, puis sous forme simplifiée.
Les premiers, c'est facile, puisque qu'on a
- la moitié gauche du tableau grisée : 50/100 = 1/2, ça, ça se voit facilement.
- idem pour le deuxième tableau, toutes les cases grisées : 100/100 = 1/1.
- Le troisième, deux colonnes grisées, ça marche toujours : 20/100 = 1/5.
Mais après, ça se complique.
3 colonnes et demi grisées : 35/100. Moi, je sais bien que ça fait 7/20. Mais là, ça ne se "voit" pas. Alors je ne vois pas comment je peux amener Fiston à simplifier l'écriture, sauf en décomposant les nombres. C'est sur cet exemple que je cale.


Je fais comment, sans décomposer ?
Là où ça se complique, c'est pour les équivalences, ou réductions de fraction.
L'exercice consiste en une série de tableaux de 10 cases par 10 cases, soit cent au total, dont une partie est grisée, partie qu'il faut traduire sous forme de fraction, d'abord sur 100, puis sous forme simplifiée.
Les premiers, c'est facile, puisque qu'on a
- la moitié gauche du tableau grisée : 50/100 = 1/2, ça, ça se voit facilement.
- idem pour le deuxième tableau, toutes les cases grisées : 100/100 = 1/1.
- Le troisième, deux colonnes grisées, ça marche toujours : 20/100 = 1/5.
Mais après, ça se complique.
3 colonnes et demi grisées : 35/100. Moi, je sais bien que ça fait 7/20. Mais là, ça ne se "voit" pas. Alors je ne vois pas comment je peux amener Fiston à simplifier l'écriture, sauf en décomposant les nombres. C'est sur cet exemple que je cale.


Je fais comment, sans décomposer ?
 V.MarchaisEmpereur
V.MarchaisEmpereur
Pierre_au_carré a écrit:V.Marchais a écrit:Frimousette, merci à toi et ton mari. Jusque là, je comprends, mais quand c'est plus complexe, comme rapport ?
Il faut vraiment que je vous scanne la feuille.
Il attend la 6ième ou la 5ième...
Ben moi je veux bien mais son exercice est pour demain, pas pour dans trois ans...
 frimoussette77Guide spirituel
frimoussette77Guide spirituel
Il faut faire 7 demi colonnes, et des demi-colonnes il y en a 20 en tout, d'où la fraction 7/20.
ça doit reposer uniquement sur "un jeu géométrique".
ça doit reposer uniquement sur "un jeu géométrique".
 V.MarchaisEmpereur
V.MarchaisEmpereur
Voilà le tableau en question.
On compte les colonnes, et on voit que c'est 35/100, OK, jusque là, pani pwoblem.
Mais comment on passe de l'observation de ce même tableau à 7/20 ?
| | | | | | | | | | |
| | | | | | | | | | |
| | | | | | | | | | |
| | | | | | | | | | |
| | | | | | | | | | |
| | | | | | | | | | |
| | | | | | | | | | |
| | | | | | | | | | |
| | | | | | | | | | |
| | | | | | | | | | |
On compte les colonnes, et on voit que c'est 35/100, OK, jusque là, pani pwoblem.
Mais comment on passe de l'observation de ce même tableau à 7/20 ?
 V.MarchaisEmpereur
V.MarchaisEmpereur
Pétard ! J'aurais pas pensé à changer d'unité.
Merci Frimousette. Je vais dire ça à Junior.
Merci Frimousette. Je vais dire ça à Junior.
- Spoiler:
- Mais je trouve plus simple de faire des divisions...
 InvitéInvité
InvitéInvité
V.Marchais a écrit:Pétard ! J'aurais pas pensé à changer d'unité.
???
Je viens de comprendre l' "unité": une unité ici = une moitié de colonne... Dur dur de faire des maths le dimanche
 frimoussette77Guide spirituel
frimoussette77Guide spirituel
J'ai répondu en même temps :lol!:Al a écrit:V.Marchais a écrit:Pétard ! J'aurais pas pensé à changer d'unité.
???
Je viens de comprendre l' "unité": une unité ici = une moitié de colonne... Dur dur de faire des maths le dimanche
 V.MarchaisEmpereur
V.MarchaisEmpereur
Frimoussette est d'autant plus forte que je me rends compte que j'ai oublié de griser une colonne dans mon tableau. :lol:
 InvitéInvité
InvitéInvité
Comment est choisi le tableau de base (nombre de lignes et de colonnes) pour simplifier une fraction quelconque?
 V.MarchaisEmpereur
V.MarchaisEmpereur
Je pense que c'est à l'élève d'observer et de trouver l'unité pertinente. Parfois, ça saute aux yeux (les moitiés, les quarts...). Là, il a fallu un peu plus d'astuce et, bon, la famille n'a pas brillé par sa pertinence, justement... 
 InvitéInvité
InvitéInvité
V.Marchais a écrit:Je pense que c'est à l'élève d'observer et de trouver l'unité pertinente.
C'est marrant, ça me fait penser aux méthodes "globales" d'apprentissage de la lecture!

 V.MarchaisEmpereur
V.MarchaisEmpereur
Je me sens totalement incompétente pour juger des méthodes employées en maths. Jusque là, ça a bien marché : Fiston comprend, non seulement il réussit mais il adore les maths.
Mais là, il ne voyait pas comment faire et si lui n'est pas capable de ré-expliquer comment la maîtresse a dit de faire, je ne vois pas comment l'aider.
Mais là, il ne voyait pas comment faire et si lui n'est pas capable de ré-expliquer comment la maîtresse a dit de faire, je ne vois pas comment l'aider.
 JPhMMDemi-dieu
JPhMMDemi-dieu
V.Marchais a écrit:Voilà le tableau en question.
On compte les colonnes, et on voit que c'est 35/100, OK, jusque là, pani pwoblem.
Mais comment on passe de l'observation de ce même tableau à 7/20 ?
En fait, il y en a 25 sur ton tableau.
Donc il s'agit de 25/100.
Question : combien y a-t-il de paquets de 5 grisés (j'ai mis un paquet de 5 en jaune grisé) ? J'en compte 5 paquets de 5 grisés sur 20 paquets de 5.
Donc 25/100 = 5 / 20
| | | | | | | | | | |
| | | | | | | | | | |
| | | | | | | | | | |
| | | | | | | | | | |
| | | | | | | | | | |
| | | | | | | | | | |
| | | | | | | | | | |
| | | | | | | | | | |
| | | | | | | | | | |
| | | | | | | | | | |
_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
 frimoussette77Guide spirituel
frimoussette77Guide spirituel
Véronique avait oublié de griser une colonne du tableau, la réponse attendue était bien 7/20.JPhMM a écrit:V.Marchais a écrit:Voilà le tableau en question.
On compte les colonnes, et on voit que c'est 35/100, OK, jusque là, pani pwoblem.
Mais comment on passe de l'observation de ce même tableau à 7/20 ?
En fait, il y en a 25 sur ton tableau.
Donc il s'agit de 25/100.
Question : combien y a-t-il de paquets de 5 grisés (j'ai mis un paquet de 5 en jaune grisé) ? J'en compte 5 paquets de 5 grisés sur 20 paquets de 5.
Donc 25/100 = 5 / 20
Page 1 sur 4 • 1, 2, 3, 4 

Permission de ce forum:
Vous ne pouvez pas répondre aux sujets dans ce forum



