 KihyaNiveau 6
KihyaNiveau 6
Bonsoir,
Je suis en train de lire des études, et je cherche une âme charitable pour m'aider à comprendre des statistiques ...
Dans cette étude, on cherche à étudier les bénéfices d'une méthode d'enseignement. J'ai deux tableaux, l'un pour le groupe témoin, l’autre pour le groupe expérimental. Dans chaque groupe, on a testé le niveau des élèves en "6th grade", puis un an plus tard en "7th grade" dans différentes matières : Tamil (un dialecte local : Inde), Anglais, Maths, Sciences, Sciences sociales.
Mean : c'est la note moyenne obtenue par les étudiants ? Un bon score = une bonne performance ?
N : le nombre d'étudiants dans l'échantillon (au moins un truc que j'ai capté )
)
Déviation standard : ok ça me rappelle des souvenirs lointains, une histoire de dispersion, tout ça ... mais est-ce pertinent pour l'analyse ?
Standard error mean : ??? Je ne vois pas
t : alors là je n'ai aucune idée de ce que cela signifie
En fait, dans l'article, l'auteur trouve que les bénéfices sont très significatifs, mais moi j'ai l'impression que la différence n'est pas énorme, et j'aimerais bien comprendre si j'ai raison ou non.
Groupe témoin :

Groupe expérimental :

Merciiii pour votre aide !
Je suis en train de lire des études, et je cherche une âme charitable pour m'aider à comprendre des statistiques ...

Dans cette étude, on cherche à étudier les bénéfices d'une méthode d'enseignement. J'ai deux tableaux, l'un pour le groupe témoin, l’autre pour le groupe expérimental. Dans chaque groupe, on a testé le niveau des élèves en "6th grade", puis un an plus tard en "7th grade" dans différentes matières : Tamil (un dialecte local : Inde), Anglais, Maths, Sciences, Sciences sociales.
Mean : c'est la note moyenne obtenue par les étudiants ? Un bon score = une bonne performance ?
N : le nombre d'étudiants dans l'échantillon (au moins un truc que j'ai capté
Déviation standard : ok ça me rappelle des souvenirs lointains, une histoire de dispersion, tout ça ... mais est-ce pertinent pour l'analyse ?
Standard error mean : ??? Je ne vois pas
t : alors là je n'ai aucune idée de ce que cela signifie
En fait, dans l'article, l'auteur trouve que les bénéfices sont très significatifs, mais moi j'ai l'impression que la différence n'est pas énorme, et j'aimerais bien comprendre si j'ai raison ou non.
Groupe témoin :

Groupe expérimental :

Merciiii pour votre aide !
 MathadorEmpereur
MathadorEmpereur
Standard deviation = écart-type, qui donne une estimation des écarts à la moyenne (avec une formule un peu tordu mais qui a ses justifications).
Standard error mean = écart-type divisé par racine de N: cela estime les fluctuations attendues de la moyenne si l'on reproduisait l'expérience avec les mêmes paramètres.
t = statistique de Student: on l'utilise dans le cadre d'un test statistique.
Un test repose sur une hypothèse nulle et une hypothèse alternative; je ne sais pas ici quelle est précisément l'hypothèse nulle (le fait que la méthode testée soit inutile ? que les élèves n'aient rien appris pendant un an ?).
Dans le cadre de l'hypothèse nulle, t est une variable aléatoire qui suit une loi de Student à environ N degrés de liberté (quand N est grand, ça se rapproche d'une loi normale centrée réduite); si la valeur est particulièrement éloignée de 0, c'est quelque chose de peu probable sous l'hypothèse nulle, et donc on en déduit que l'hypothèse nulle est fausse avec peu de chance de se tromper.
Pour les statistiques en **, on a p<0,01, ce qui veut dire qu'une telle valeur (supérieure ou égale à celle observée) aurait moins d'une chance sur 100 d'être observée si l'hypothèse nulle était vérifiée.
Standard error mean = écart-type divisé par racine de N: cela estime les fluctuations attendues de la moyenne si l'on reproduisait l'expérience avec les mêmes paramètres.
t = statistique de Student: on l'utilise dans le cadre d'un test statistique.
Un test repose sur une hypothèse nulle et une hypothèse alternative; je ne sais pas ici quelle est précisément l'hypothèse nulle (le fait que la méthode testée soit inutile ? que les élèves n'aient rien appris pendant un an ?).
Dans le cadre de l'hypothèse nulle, t est une variable aléatoire qui suit une loi de Student à environ N degrés de liberté (quand N est grand, ça se rapproche d'une loi normale centrée réduite); si la valeur est particulièrement éloignée de 0, c'est quelque chose de peu probable sous l'hypothèse nulle, et donc on en déduit que l'hypothèse nulle est fausse avec peu de chance de se tromper.
Pour les statistiques en **, on a p<0,01, ce qui veut dire qu'une telle valeur (supérieure ou égale à celle observée) aurait moins d'une chance sur 100 d'être observée si l'hypothèse nulle était vérifiée.
_________________
"There are three kinds of lies: lies, damned lies, and statistics." (cité par Mark Twain)
« Vulnerasti cor meum, soror mea, sponsa; vulnerasti cor meum in uno oculorum tuorum, et in uno crine colli tui.
Quam pulchrae sunt mammae tuae, soror mea sponsa! pulchriora sunt ubera tua vino, et odor unguentorum tuorum super omnia aromata. » (Canticum Canticorum 4:9-10)
 ben2510Expert spécialisé
ben2510Expert spécialisé
Il s'agit de statistiques inférentielles, plus précisément d'un test de comparaison de moyennes sur échantillons indépendants, appelé communément "t de Student" car la statistique calculée suit une loi de probabilité appelée loi de Student.
Standard deviation c'est l'écart type, qui effectivement mesure la dispersion des notes à l'intérieur de chaque condition.
Standard error mean c'est l'erreur type, définie comme l'écart type divisé par la racine carrée de l'effectif.
Si la valeur de t est "loin de zéro" alors on conclut qu'il y a une différence significative entre les deux groupes, le nombre d'étoiles à côté de la valeur de t donne la "significativité", une étoile signifie que la probabilité d'être aussi loin de zéro seulement à cause du hasard est inférieure à une chance sur 20 (p<0,05), et deux étoiles inférieure à une chance sur 100 (p<0,01).
Cherche un cours de stats inférentielles en ligne, de niveau L1/L2 en médecine, biologie ou psychologie (ou MIASHS).
Tu peux aussi chercher un collègue qui enseigne les maths en BTS, ce chapitre est présent dans de nombreuses séries de BTS.
Ceci dit je suis plutôt d'accord avec toi, pour chaque paire de moyennes comparées de la 6e à la 7e année, les différences de moyennes semblent très proches pour la condition témoin et pour la condition expérimentale. Il me semble qu'ici des t de Student sont peu appropriés, une ANOVA à deux facteurs serait plus adaptée je pense (Mathador tu en dis quoi ?)
Standard deviation c'est l'écart type, qui effectivement mesure la dispersion des notes à l'intérieur de chaque condition.
Standard error mean c'est l'erreur type, définie comme l'écart type divisé par la racine carrée de l'effectif.
Si la valeur de t est "loin de zéro" alors on conclut qu'il y a une différence significative entre les deux groupes, le nombre d'étoiles à côté de la valeur de t donne la "significativité", une étoile signifie que la probabilité d'être aussi loin de zéro seulement à cause du hasard est inférieure à une chance sur 20 (p<0,05), et deux étoiles inférieure à une chance sur 100 (p<0,01).
Cherche un cours de stats inférentielles en ligne, de niveau L1/L2 en médecine, biologie ou psychologie (ou MIASHS).
Tu peux aussi chercher un collègue qui enseigne les maths en BTS, ce chapitre est présent dans de nombreuses séries de BTS.
Ceci dit je suis plutôt d'accord avec toi, pour chaque paire de moyennes comparées de la 6e à la 7e année, les différences de moyennes semblent très proches pour la condition témoin et pour la condition expérimentale. Il me semble qu'ici des t de Student sont peu appropriés, une ANOVA à deux facteurs serait plus adaptée je pense (Mathador tu en dis quoi ?)
_________________
On fait la science avec des faits, comme on fait une maison avec des pierres : mais une accumulation de faits n'est pas plus une science qu'un tas de pierres n'est une maison. Henri Poincaré La notion d'équation différentielle est le pivot de la conception scientifique du monde. Vladimir Arnold
 MathadorEmpereur
MathadorEmpereur
C'est ce que j'ai cru aussi au début, mais la légende du tableau indique "Paired samples t-test" ce qui désigne, si j'en crois Wikipédia, un test où l'on fait un appariement entre les deux échantillons: https://en.wikipedia.org/wiki/Paired_difference_testben2510 a écrit:Il s'agit de statistiques inférentielles, plus précisément d'un test de comparaison de moyennes sur échantillons indépendants, appelé communément "t de Student" car la statistique calculée suit une loi de probabilité appelée loi de Student.
Ce ne sera pas évident de le trouver dans une école primaireben2510 a écrit:Tu peux aussi chercher un collègue qui enseigne les maths en BTS, ce chapitre est présent dans de nombreuses séries de BTS.

_________________
"There are three kinds of lies: lies, damned lies, and statistics." (cité par Mark Twain)
« Vulnerasti cor meum, soror mea, sponsa; vulnerasti cor meum in uno oculorum tuorum, et in uno crine colli tui.
Quam pulchrae sunt mammae tuae, soror mea sponsa! pulchriora sunt ubera tua vino, et odor unguentorum tuorum super omnia aromata. » (Canticum Canticorum 4:9-10)
 ben2510Expert spécialisé
ben2510Expert spécialisé
Oui tu as raison Mathador, les échantillons sont appariés, ce sont les mêmes élèves qui sont suivis de la 6e à la 7e année.
_________________
On fait la science avec des faits, comme on fait une maison avec des pierres : mais une accumulation de faits n'est pas plus une science qu'un tas de pierres n'est une maison. Henri Poincaré La notion d'équation différentielle est le pivot de la conception scientifique du monde. Vladimir Arnold
 beaverforeverNeoprof expérimenté
beaverforeverNeoprof expérimenté
Peut-être que l'hypothèse nulle est infirmée mais que taille d'effet est très faible. Est-ce que les auteurs ont calculé un d de Cohen dans la suite de l'article ?
 KihyaNiveau 6
KihyaNiveau 6
Merci pour vos explications !
Non, la suite de l'article c'est "Voila voila grâce à mon expérimentation on observe des énoooorme progrès dans toutes les matières, sauf le Tamil" puis une brève discussion des résultats (questionnement sur la composition des groupes), et c'est tout.
Je trouve son interprétation un peu légère, et je n'étais pas d'accord sur les sciences par exemple : entre le 6th grade et le 7th grade, les élèves du groupe témoin ont vu leurs résultats augmenter en moyenne de 4.27 points, mais ceux du groupe expérimental que de 3.9 points. Les élèves du groupe témoin ont donc eu une meilleure progression que ceux du groupe expérimental
Les élèves du groupe témoin ont donc eu une meilleure progression que ceux du groupe expérimental
Et l'énooorme progression me semble exagérée : si les moyennes ("Mean") sont sur 100 points, l'écart des progrès entre le groupe témoin et le groupe expérimental n'est pas phénoménal, environ 1% de différence (de plus ou de moins selon les matières). Ça ne me semble pas significatif
Surtout que cette année je retombe en grande section Je peux vous donner des conseils concernant la fabrication d'objets de Noël ou sur la marque de pâte à modeler qui-ne-colle-pas-trop-aux-doigts-mais-qui-est-quand-même-malléable, mais niveau statistiques, c'est le désert absolu
Je peux vous donner des conseils concernant la fabrication d'objets de Noël ou sur la marque de pâte à modeler qui-ne-colle-pas-trop-aux-doigts-mais-qui-est-quand-même-malléable, mais niveau statistiques, c'est le désert absolu 


Peut-être que l'hypothèse nulle est infirmée mais que taille d'effet est très faible. Est-ce que les auteurs ont calculé un d de Cohen dans la suite de l'article ?
Non, la suite de l'article c'est "Voila voila grâce à mon expérimentation on observe des énoooorme progrès dans toutes les matières, sauf le Tamil" puis une brève discussion des résultats (questionnement sur la composition des groupes), et c'est tout.
Je trouve son interprétation un peu légère, et je n'étais pas d'accord sur les sciences par exemple : entre le 6th grade et le 7th grade, les élèves du groupe témoin ont vu leurs résultats augmenter en moyenne de 4.27 points, mais ceux du groupe expérimental que de 3.9 points.
 Les élèves du groupe témoin ont donc eu une meilleure progression que ceux du groupe expérimental
Les élèves du groupe témoin ont donc eu une meilleure progression que ceux du groupe expérimentalEt l'énooorme progression me semble exagérée : si les moyennes ("Mean") sont sur 100 points, l'écart des progrès entre le groupe témoin et le groupe expérimental n'est pas phénoménal, environ 1% de différence (de plus ou de moins selon les matières). Ça ne me semble pas significatif

Tu peux aussi chercher un collègue qui enseigne les maths en BTS, ce chapitre est présent dans de nombreuses séries de BTS.
Ce ne sera pas évident de le trouver dans une école primaire Wink
Surtout que cette année je retombe en grande section
 Je peux vous donner des conseils concernant la fabrication d'objets de Noël ou sur la marque de pâte à modeler qui-ne-colle-pas-trop-aux-doigts-mais-qui-est-quand-même-malléable, mais niveau statistiques, c'est le désert absolu
Je peux vous donner des conseils concernant la fabrication d'objets de Noël ou sur la marque de pâte à modeler qui-ne-colle-pas-trop-aux-doigts-mais-qui-est-quand-même-malléable, mais niveau statistiques, c'est le désert absolu  MathadorEmpereur
MathadorEmpereur
Mais du coup, en maths et en sciences sociales, les élèves régressent ?Kihya a écrit:Je trouve son interprétation un peu légère, et je n'étais pas d'accord sur les sciences par exemple : entre le 6th grade et le 7th grade, les élèves du groupe témoin ont vu leurs résultats augmenter en moyenne de 4.27 points, mais ceux du groupe expérimental que de 3.9 points.Les élèves du groupe témoin ont donc eu une meilleure progression que ceux du groupe expérimental
Surtout quand on rapporte cela aux écart-types d'environ 15, ce qui correspond (si je ne fais pas de gros contre-sens) à des tailles d'effet autour de 0,07. Si je compare à cela: https://visible-learning.org/hattie-ranking-influences-effect-sizes-learning-achievement/ c'est que dalle.Kihya a écrit:Et l'énooorme progression me semble exagérée : si les moyennes ("Mean") sont sur 100 points, l'écart des progrès entre le groupe témoin et le groupe expérimental n'est pas phénoménal, environ 1% de différence (de plus ou de moins selon les matières). Ça ne me semble pas significatif
_________________
"There are three kinds of lies: lies, damned lies, and statistics." (cité par Mark Twain)
« Vulnerasti cor meum, soror mea, sponsa; vulnerasti cor meum in uno oculorum tuorum, et in uno crine colli tui.
Quam pulchrae sunt mammae tuae, soror mea sponsa! pulchriora sunt ubera tua vino, et odor unguentorum tuorum super omnia aromata. » (Canticum Canticorum 4:9-10)
 beaverforeverNeoprof expérimenté
beaverforeverNeoprof expérimenté
Dans la plupart des publications, on ne fait pas la comparaison ainsi. En effet, un moyenne est dépendante des valeurs extrêmes qui la compose, ce qui peut fausser l'information à extraire des données : peut-être qu'un seul élève a beaucoup progressé ou beaucoup régressé et qu’il fausse l’essentielle de l’information qui concerne l’ensemble des élèves qui ont pu stagner ou un peu progresser par exemple.Kihya a écrit:Je trouve son interprétation un peu légère, et je n'étais pas d'accord sur les sciences par exemple : entre le 6th grade et le 7th grade, les élèves du groupe témoin ont vu leurs résultats augmenter en moyenne de 4.27 points, mais ceux du groupe expérimental que de 3.9 points.Les élèves du groupe témoin ont donc eu une meilleure progression que ceux du groupe expérimental
C’est pourquoi on divise la progression par l’écart type, pour rendre les progressions plus comparable quand on cherche à évaluer la taille d’effet.
Ici on a :
D (de Cohen) = (59,99 – 55,72)/19,4 = 4.27/19,4 = 0,22
(J’ai pris le plus grand écart type pour être le plus conservateur possible, si on prend le plus petit on obtient 0,27 ce qui ne change pas l’ordre de grandeur.)
0,22 de taille d’effet, ce n’est pas foufou, c’est plutôt une taille d’effet faible et cela traduit plutôt une intervention médiocrement efficace. On parle d’une taille d’effet moyenne autour de 0,4 et de taille d’effet forte entre 0,6 et 1,5.
Il faut faire attention à la formulation « statistiquement significatif », car, intuitivement, on pense qu’il s’agit d’une information importante et utile, alors qu’une petite valeur p signifie seulement que la différence observée n’est sans doute pas due au hasard. Ici, on a un cas de différence statistiquement significative, mais dont la taille d’effet (sous réserver d’avoir compris la méthodologie de l’article) est semble-t-il médiocre.Et l'énooorme progression me semble exagérée : si les moyennes ("Mean") sont sur 100 points, l'écart des progrès entre le groupe témoin et le groupe expérimental n'est pas phénoménal, environ 1% de différence (de plus ou de moins selon les matières). Ça ne me semble pas significatif
- Comment calculer une taille d'effet:
- Rendre visible la progression de vos élève par la taille d’effet
ou
Comment calculer si vos élèves progressent lentement ou rapidement ?
(ou)
(Comment savoir si vos pratiques professionnelles sont médiocres, moyennes ou excellentes ?) (Gasp !)
Vos élèves progressent, mais :
comment savoir s’ils progressent plus ou moins que les autres ?
comment mesurer l’efficacité de vos méthodes pédagogiques ?
La taille d’effet compare statistiquement les progressions. Popularisée par John Hattie dans son livre Visible learning, publié en 2009, elle mesure la progression d’une classe et la compare à d’autres classes. L’enseignant a une information fondamentale : il sait si ses pratiques font progresser rapidement ses élèves. Il a une boussole pour orienter ses choix et améliorer sa pratique.
Qu’est-ce qu’une taille d’effet ?
La taille d’effet calcule, en écart type, la progression entre deux évaluations successives et similaires. Si vous avez évalué vos élèves en cartographie, vous avez une série de notes pour cette évaluation 1. Après un nouveau cours, vous faites une évaluation 2. Les deux évaluations sont très proches, voire identiques.
Alors, vous pouvez calculer la taille d’effet selon cette formule :
Taille d'effet=(Moyenne (évaluation 2)- Moyenne (évaluation 1))/(Écart type)
L’écart type peut être soit celui de l’évaluation 1, de l’évaluation 2, de l’ensemble des deux séries de notes, voire (si vous utilisez une évaluation standardisée qui a été réalisée sur un grand nombre d’élèves) celui d’une très grande série de notes obtenues par d’autres élèves à la même évaluation. Mon conseil est de prendre la valeur la plus élevée, pour être le plus prudent possible.
Si la différence entre les deux moyennes n’était pas divisée par l’écart type, l’enseignant n’aurait qu’un écart en points propre aux deux évaluations données. Peut-être que les moyennes en cartographie sont plus élevées qu’en analyse de document. Si les élèves progressent de deux points en cartographie et de un point en analyse, comment comparer ces écarts ? En supposant que les notes de chaque évaluation ont une distribution normale, la division par l’écart type mesure le déplacement, en nombre d’écart type, entre les deux distributions. La progression est alors exprimée en écart type, ce qui permet de les comparer dans une unité commune. Si les élèves progressent de 0.2 écart type en cartographie et de 0.8 en analyse de document, je peux être plus confiant pour dire qu’ils progressent plus vite dans le second exercice.
Pour calculer une taille d’effet crédible, il faut au minimum une trentaine de notes et si possible soixante-dix ou plus.
Comment interpréter une taille d’effet ?
Les études portant sur de nombreux élèves et les méta-analyses montrent que la progression moyenne d’un élève sur une année correspond à une taille d’effet de 0,40.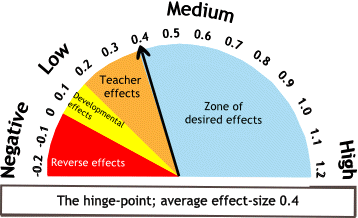
Une taille d’effet négative de la classe est un signal fort et rare qu’un enseignement a échoué. Elle doit être un signal d’alerte pour l’enseignant. Une taille d’effet entre 0 et 0,15, indique une progression médiocre, ce qui doit faire l’objet d’une analyse de l’enseignant car son apport a été faible. Une progression entre 0,15 et 0.4 indique un effet moyen d’un enseignant sur les résultats de ses élèves. Au-dessus, la progression peut être considérée comme rapide et éventuellement comme le résultat d’une meilleure pratique professionnelle. Les progressions sont souvent plus rapides dans le primaire que dans le secondaire.
Comment calculer une taille d’effet individuelle ?
On peut aussi calculer une taille d’effet individuelle :
Taille d'effet=(Note (évaluation 2)-Note(évaluation 1))/(Écart type de la classe)
Cette taille d’effet mesure l’évolution de l’élève. Cette information est moins pertinente que la taille d’effet du groupe et ne doit pas être surinterprétée.
Que faire de ces données ?
La taille d’effet est une échelle d’efficacité professionnelle plus objective que les estimations utilisées dans l’Éducation nationale, comme une augmentation de moyenne trimestrielle. Ces données questionnent les pratiques de l’enseignant et l’oriente dans son amélioration.
Cette méthode est peu compatible avec les pratiques habituelles dans l’Éducation nationale, où les élèves sont souvent évalués une seule fois, de façon sommative, à la fin de leur apprentissage, ce qui empêche de mesurer une progression. Toutefois, il est possible d’intégrer ce type de mesure en mettant en œuvre des évaluations diagnostiques et formatives, et en réduisant et espaçant les évaluations sommatives. L’enseignant peut alors calculer la progression de ses élèves.
La taille d’effet rend visible la progression des élèves. L’enseignant ne voit plus Stanislas comme un élève en échec, mais comme un élève qui a beaucoup progressé, en augmentant ses résultats de 1.2 écart type, même si sa moyenne trimestrielle reste de 7,6/20. La classe de seconde C a peut-être une moyenne de 10.06/20 en histoire géographie, mais elle a progressé de 0,7 écart type en analyse de document, elle s’est donc améliorée deux fois plus vite que la moyenne des élèves français. Mesurer la taille d’effet focalise l’attention de l’enseignant sur les élèves aux résultats faibles et à la progression lente. En voyant les progrès des élèves, la vision du métier change.
Sources:
Hattie, John, 2008, Visible Learning: A Synthesis of Over 800 Meta-Analyses Relating to Achievement. NY: Routledge. p. 392
Hattie, John A., 2011, Visible Learning for Teachers: Maximizing Impact on Learning.
Une explication en détail sur la taille d’effet.
http://www.nzcer.org.nz/system/files/16886.pdf
Un calculateur de taille d’effet en ligne
http://www.uccs.edu/~lbecker/
« C’est la taille d’effet, triple buse ! »
http://www.cem.org/attachments/ebe/ESguide.pdf
Permission de ce forum:
Vous ne pouvez pas répondre aux sujets dans ce forum




