Page 1 sur 2 • 1, 2 

 PEGUILLANNiveau 2
PEGUILLANNiveau 2
Expliquer à un élève de CM2 comment intercaler une fraction entre deux entiers successifs autres que 0 et 1 .Quelle peut-être la démarche pédagogique la plus simple s'il n'a pas encore revu les multiples et les diviseurs .Je serais heureux que vous puissiez me conseiller .Je vous en remercie à l'avance .
 ycombeMonarque
ycombeMonarque
Il n'y a pas de voie royale en mathématiques.
Si on doit enseigner, il faut faire les choses correctement: les multiples et diviseurs doivent être maîtrisés avant cette question.
Sinon on donne des "trucs" permettant de répondre à la question, mais il n'en restera pas grand chose sur le long terme.
Si on doit enseigner, il faut faire les choses correctement: les multiples et diviseurs doivent être maîtrisés avant cette question.
Sinon on donne des "trucs" permettant de répondre à la question, mais il n'en restera pas grand chose sur le long terme.
_________________
Assurbanipal: "Passant, mange, bois, divertis-toi ; tout le reste n’est rien".
Franck Ramus : "Les sciences de l'éducation à la française se font fort de produire un discours savant sur l'éducation, mais ce serait visiblement trop leur demander que de mettre leur discours à l'épreuve des faits".
 CeladonDemi-dieu
CeladonDemi-dieu
Ce sont toutes des fractions dont le numérateur est sup au dénominateur, donc.
Tu peux prendre des bandes de papier dont tu dotes les extrémités des chiffres 0; 1; 2; 3; 4; 5
Tu travailles avec les 1/2 pour commencer et tu fais exprimer 1 etc en demis. Je suppose que cette étape ne va pas poser pb.
Puis tu proposes une fraction en demis, comme 5/2. L'enfant situera sa place entre 4/2 et 6/2, donc entre 2 et 3.
Fais lui écrire 2<5/2<3.
Procède de même avec d'autres dénominateurs.
Ceci dit, complètement OK avec Ycombe. Je n'ai jamais abordé les fractions sans avoir vu multiples et diviseurs.
Tu peux prendre des bandes de papier dont tu dotes les extrémités des chiffres 0; 1; 2; 3; 4; 5
Tu travailles avec les 1/2 pour commencer et tu fais exprimer 1 etc en demis. Je suppose que cette étape ne va pas poser pb.
Puis tu proposes une fraction en demis, comme 5/2. L'enfant situera sa place entre 4/2 et 6/2, donc entre 2 et 3.
Fais lui écrire 2<5/2<3.
Procède de même avec d'autres dénominateurs.
Ceci dit, complètement OK avec Ycombe. Je n'ai jamais abordé les fractions sans avoir vu multiples et diviseurs.
 PEGUILLANNiveau 2
PEGUILLANNiveau 2
Tout à fait d'accord avec vous ,j ai procédé de la même manière en transformant les nombres entiers en fractions DONT le dénominateur est 2 ,3 ou même 10 mais c'est loin d'être gagné !! Je pense que plusieurs exercices ou manipulations pourront être très utiles .
Merci pour votre réponse rapide .
Merci pour votre réponse rapide .
 ycombeMonarque
ycombeMonarque
C'est d'autant plus difficile à gagner que les multiples ne sont pas maîtrisés.PEGUILLAN a écrit:Tout à fait d'accord avec vous ,j ai procédé de la même manière en transformant les nombres entiers en fractions DONT le dénominateur est 2 ,3 ou même 10 mais c'est loin d'être gagné !! Je pense que plusieurs exercices ou manipulations pourront être très utiles .
Merci pour votre réponse rapide .
_________________
Assurbanipal: "Passant, mange, bois, divertis-toi ; tout le reste n’est rien".
Franck Ramus : "Les sciences de l'éducation à la française se font fort de produire un discours savant sur l'éducation, mais ce serait visiblement trop leur demander que de mettre leur discours à l'épreuve des faits".
 CeladonDemi-dieu
CeladonDemi-dieu
Qu'est-ce qui t'empêche de voir les multiples et les diviseurs avec lUI comme préalable ? Les tables de x non maîtrisées ?
 ycombeMonarque
ycombeMonarque
Beaucoup de pays (dont Singapour) utilisent pour les fractions supérieure à 1 une écriture en "nombre mixte", comme on dit dans le manuel de Singapour:
5/2 c'est 2+1/2 (écrit 2 1/2) sans le '+' (écrits en fractions).
Mais pour passer une fraction "impropre" (comme chez nous) à un nombre mixte, on a quand même besoin des diviseurs:
5/2 c'est 2+1/2 (écrit 2 1/2) sans le '+' (écrits en fractions).
Mais pour passer une fraction "impropre" (comme chez nous) à un nombre mixte, on a quand même besoin des diviseurs:
_________________
Assurbanipal: "Passant, mange, bois, divertis-toi ; tout le reste n’est rien".
Franck Ramus : "Les sciences de l'éducation à la française se font fort de produire un discours savant sur l'éducation, mais ce serait visiblement trop leur demander que de mettre leur discours à l'épreuve des faits".
 jaybeNiveau 9
jaybeNiveau 9
Celadon a écrit:Qu'est-ce qui te prend, Jonjon ? 5x 2 = 13 ?
jonjon71 ne faisait que réécrire ce qu'il a vu dans la vidéo. Et même réaction :
_________________
Les mathématiciens ne sont pas des gens qui trouvent les mathématiques faciles ; comme tout le monde, ils savent qu'elles sont difficiles, mais ça ne leur fait pas peur !
 CeladonDemi-dieu
CeladonDemi-dieu
oH misère, je n'ai même pas vu la video ! 
Ah oui, quand même... je me demande dans quel état le pauvre élève ressort d'une pareille "leçon" qui s'apparente davantage à une mise bout à bout de trucs et ficelles/pensée magique qu'à un enseignement structuré procédant du b.a ba. :shock:
Ah oui, quand même... je me demande dans quel état le pauvre élève ressort d'une pareille "leçon" qui s'apparente davantage à une mise bout à bout de trucs et ficelles/pensée magique qu'à un enseignement structuré procédant du b.a ba. :shock:
 fullmetalchemistNiveau 6
fullmetalchemistNiveau 6
jonjon71 a écrit:5 x 2 = 10 + ? = 13
C'est le genre de trucs que je vois assez souvent sur des copies: des signes "=" de partout utilisés n'importe comment -_-" Cette citation en est un exemple...
 CeladonDemi-dieu
CeladonDemi-dieu
Oui, moi non plus, en CM2 je n'ai jamais réussi à faire comprendre les impossibilités d'emploi du signe =.fullmetalchemist a écrit:jonjon71 a écrit:5 x 2 = 10 + ? = 13
C'est le genre de trucs que je vois assez souvent sur des copies: des signes "=" de partout utilisés n'importe comment -_-" Cette citation en est un exemple...
 VinZTDoyen
VinZTDoyen
Celadon a écrit:Oui, moi non plus, en CM2 je n'ai jamais réussi à faire comprendre les impossibilités d'emploi du signe =.fullmetalchemist a écrit:jonjon71 a écrit:5 x 2 = 10 + ? = 13
C'est le genre de trucs que je vois assez souvent sur des copies: des signes "=" de partout utilisés n'importe comment -_-" Cette citation en est un exemple...
Si ça peut te rassurer, ce n'est pas rare en terminale.
Euh, en fait cela n'a rien de rassurant …
_________________
« Il ne faut pas croire tout ce qu'on voit sur Internet » Victor Hugo.
« Le con ne perd jamais son temps. Il perd celui des autres. » Frédéric Dard
« Ne jamais faire le jour même ce que tu peux faire faire le lendemain par quelqu'un d'autre » Pierre Dac
« Je n'ai jamais lâché prise !» Claude François
« Un économiste est un expert qui saura demain pourquoi ce qu'il avait prédit hier ne s'est pas produit aujourd'hui. » Laurence J. Peter
 pistorNiveau 5
pistorNiveau 5
Euh, ne serait ce pas une bonne idée d'abandonner les fractions impropres et de se rallier aux nombres mixtes comme dit plus haut?
Pour se raccrocher au sens des fractions , des pourcentages, des proportions.........
@ycombe c'est le cas à Singapour , en Chine aussi et dans quels autres pays selon vous ?
Pour se raccrocher au sens des fractions , des pourcentages, des proportions.........
@ycombe c'est le cas à Singapour , en Chine aussi et dans quels autres pays selon vous ?
 jaybeNiveau 9
jaybeNiveau 9
pistor a écrit:Euh, ne serait ce pas une bonne idée d'abandonner les fractions impropres
Euh, non.
_________________
Les mathématiciens ne sont pas des gens qui trouvent les mathématiques faciles ; comme tout le monde, ils savent qu'elles sont difficiles, mais ça ne leur fait pas peur !
 ycombeMonarque
ycombeMonarque
Québec (c.f. la vidéo).pistor a écrit:Euh, ne serait ce pas une bonne idée d'abandonner les fractions impropres et de se rallier aux nombres mixtes comme dit plus haut?
Pour se raccrocher au sens des fractions , des pourcentages, des proportions.........
@ycombe c'est le cas à Singapour , en Chine aussi et dans quels autres pays selon vous ?
Les US puisqu'il y en a dans la khan academy
https://www.khanacademy.org/math/arithmetic-home/arith-review-fractions/mixed-number/v/changing-an-improper-fraction-to-a-mixed-number
Après je ne sais pas.
_________________
Assurbanipal: "Passant, mange, bois, divertis-toi ; tout le reste n’est rien".
Franck Ramus : "Les sciences de l'éducation à la française se font fort de produire un discours savant sur l'éducation, mais ce serait visiblement trop leur demander que de mettre leur discours à l'épreuve des faits".
 jaybeNiveau 9
jaybeNiveau 9
1 3/5 fois 2 1/3 fois 4 1/2 fois 3 1/3 = ?
\frac{8}{5} \times \frac{7}{3} \times \frac{9}{2} \times \frac{10}{3} = ?
(désolé pour cette grosse flemme de délatexifier... si je trouve comment faire joli, j'édite, promis !)
\frac{8}{5} \times \frac{7}{3} \times \frac{9}{2} \times \frac{10}{3} = ?
(désolé pour cette grosse flemme de délatexifier... si je trouve comment faire joli, j'édite, promis !)
_________________
Les mathématiciens ne sont pas des gens qui trouvent les mathématiques faciles ; comme tout le monde, ils savent qu'elles sont difficiles, mais ça ne leur fait pas peur !
 pistorNiveau 5
pistorNiveau 5
argument recevable .
mais comment font les Singapouriens ?
y-a-t-il une transition entre les deux écritures? école-collège- lycée?
mais comment font les Singapouriens ?
y-a-t-il une transition entre les deux écritures? école-collège- lycée?
 jaybeNiveau 9
jaybeNiveau 9
D'après une rapide recherche sur le net, on trouve beaucoup d'exercices de conversion dans les deux sens pour les élèves de 5è et 6è grade, donc je suppose que le lien entre les deux écritures arrive relativement vite et que les élèves continuent par la suite à manipuler les deux formes. Peut-être quelqu'un pourra apporter davantage de précisions ?
_________________
Les mathématiciens ne sont pas des gens qui trouvent les mathématiques faciles ; comme tout le monde, ils savent qu'elles sont difficiles, mais ça ne leur fait pas peur !
 pistorNiveau 5
pistorNiveau 5
Ok merci, il n'empêche qu'en effet les fractions impropres peuvent être perturbantes pour les petites classes (selon moi)
 FlorettebataveNiveau 5
FlorettebataveNiveau 5
Les fractions mixtes sont utilisées aussi au Royaume-Uni (programme abacus en primaire) et dans les écoles internationales.
Il y a des chances que cela concerne tout le monde anglo-saxon.
Ils commencent les fractions dès la grande section (Year1), de manière très visuelle avec des parts de pizzas, pour atteindre les fractions mixtes en Year5 (CM1).
Voici un exemple des exercices faits en primaire sur plusieurs niveaux
http://www.pearsonschoolsandfecolleges.co.uk/Primary/Mathematics/AllMathematicsresources/Abacus/Samples/WorkbooksandTextbooks/AbacusTextbookandWorkbookSampleBooklet.pdf
Ils arrivent assez facilement à comprendre la logique du truc avec beaucoup d'exercices de ce type (niveau CM1)
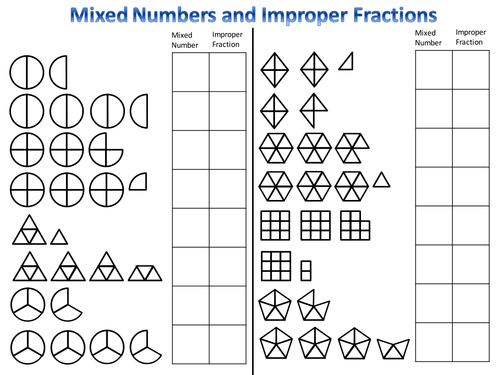
Et assez rapidement ils peuvent dire que 19/7= 2 5/7 est donc plus grand que 21/11= 1 10/11
Il y a des chances que cela concerne tout le monde anglo-saxon.
Ils commencent les fractions dès la grande section (Year1), de manière très visuelle avec des parts de pizzas, pour atteindre les fractions mixtes en Year5 (CM1).
Voici un exemple des exercices faits en primaire sur plusieurs niveaux
http://www.pearsonschoolsandfecolleges.co.uk/Primary/Mathematics/AllMathematicsresources/Abacus/Samples/WorkbooksandTextbooks/AbacusTextbookandWorkbookSampleBooklet.pdf
Ils arrivent assez facilement à comprendre la logique du truc avec beaucoup d'exercices de ce type (niveau CM1)

Et assez rapidement ils peuvent dire que 19/7= 2 5/7 est donc plus grand que 21/11= 1 10/11
 ben2510Expert spécialisé
ben2510Expert spécialisé
jaybe a écrit:1 3/5 fois 2 1/3 fois 4 1/2 fois 3 1/3 = ?
\frac{8}{5} \times \frac{7}{3} \times \frac{9}{2} \times \frac{10}{3} = ?
(désolé pour cette grosse flemme de délatexifier... si je trouve comment faire joli, j'édite, promis !)
Avec http://www.astronet.ru/db/latex2gif/ tu récupères ce gif :

En ce qui concerne les fractions mixtes, une simple référence à la voie 93/4 d'une certain gare londonienne aide beaucoup les élèves, surtout quand il est 11h3/4 et qu'ils ont faim ;-)
Il faut juste leur dire qu'ici 93/4 désigne 9+3/4 et pas 9*3/4 puisqu'habituellement l'absence de symbole opératoire dénote une multiplication.
D'ailleurs avant l'utilisation de la virgule comme séparateur décimal, 3,14 s'écrivait
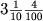
_________________
On fait la science avec des faits, comme on fait une maison avec des pierres : mais une accumulation de faits n'est pas plus une science qu'un tas de pierres n'est une maison. Henri Poincaré La notion d'équation différentielle est le pivot de la conception scientifique du monde. Vladimir Arnold
Page 1 sur 2 • 1, 2 

- [espagnol] eTwinning : des "étudiants sans frontières"
- Les enfants autistes, « oubliés de la rentrée » dénonce Austistes sans frontières
- (LV) travailler sans videoproj, sans connexion et sans audio
- Comment lutter contre des classes sans note imposées sans concertation/formation ?
- expliquer les fractions
Permission de ce forum:
Vous ne pouvez pas répondre aux sujets dans ce forum



