 gmsl65.Niveau 2
gmsl65.Niveau 2
Bonjour,
J'ai une classe de quatrième pour la première fois.
Je me pose donc des questions didactiques.
J'ai vu des progressions qui commençaient par le produit de nombres relatifs (en rappelant en amont l'addition et la soustraction vues en 5ème). Or pour justifier la règle de signes, on a besoin de la simple distributivité. Mais en 5ème on ne parle pas de distributivité.
Je me demandais donc comment certains d'entre vous faisiez si vous enseignez la règle des signes d'un produit avant la distributivité.
Merci.
J'ai une classe de quatrième pour la première fois.
Je me pose donc des questions didactiques.
J'ai vu des progressions qui commençaient par le produit de nombres relatifs (en rappelant en amont l'addition et la soustraction vues en 5ème). Or pour justifier la règle de signes, on a besoin de la simple distributivité. Mais en 5ème on ne parle pas de distributivité.
Je me demandais donc comment certains d'entre vous faisiez si vous enseignez la règle des signes d'un produit avant la distributivité.
Merci.
 chmarmottineGuide spirituel
chmarmottineGuide spirituel
On fait la distributivité en 5e.
 X.Y.U.Niveau 7
X.Y.U.Niveau 7
Je trouve la démo avec la distribution assez lourde, je procède autrement (et je le fais en classe dialoguée, avant c'était activité de découverte en individuel mais certains sont largués dès le début, alors je préfère ne pas perdre de temps, faire une découverte rapide sans forcément qu'ils notent de trace écrite, mais je sollicite bien l'attention de tout le monde si je vois que ça décroche, ça me fait gagner du temps que je consacre ensuite à vérifier rapidement que c'est compris en interrogeant un max d'élèves sur plein de ptits calculs de bases).
Au tableau, je leur demande comment ils ont appris à faire 5x3 quand ils étaient petits (ça les fait sourire de fouiller dans leurs souvenirs). Ils vont me dire par exemple 5+5+5, et le résultat. Je note les calculs en même temps.
Sur une autre ligne, je leur dis "eh bien on va s'en servir pour essayer de deviner le résultat de (-5)x3". (si jamais ils avaient proposé 3+3+3+3+3, je leur demande plutôt 5x(-3), du coup). On écrit donc (-5)x3 = (-5)+(-5)+(-5) = -15.
Et si c'était 4x(-3) ? Ils proposent assez spontanément de faire une somme de facteurs (-3).
Mais alors si on a (-4)x(-8) ? Certains vont proposer -32, d'autres 32, d'autres on ne peut pas savoir... Comme ils ne sont pas d'accord, je leur propose d'écrire la table du (-8) et de la poursuivre :
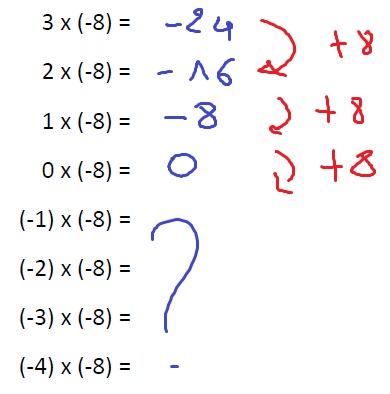
on trouve les résultats en bleu facilement puisqu'on vient de comprendre comment ça marchait quand on multipliait un positif par un négatif. Puis je leur demande de trouver une logique pour passer d'un résultat au suivant, on me dit qu'on enlève 8 (y en a toujours pour se planter), mais on remarque assez vite qu'en fait on ajoute 8 (par exemple -24 + 8 = -16), et donc j'ajoute les opérateurs en rouge sur le côté. Et on prolonge le raisonnement du côté des facteurs négatifs, et ooooh, ils sont tout contents de remarquer que le résultat est en fait tout simple à trouver. On résume tout de suite schématiquement au tableau avec :
(+)x(+) -> +
(-)x(-) -> +
(+)x(-) -> -
(-)x(+) -> -
et là il y en a toujours un pour avoir un éclair de lucidité et me lancer spontanément "oh mais c'est la même règle des signes que quand on retire les parenthèses !!" (ou sinon je leur tends un peu la perche ), et là je leur dis "mais oui, c'est encore plus facile qu'on ne croit puisqu'on la connaît déjà un peu, cette règle !", tout en concluant par "concernant les relatifs, vous avez fait le plus dur avec les additions et soustractions, vous allez voir que le reste est plus simple".
), et là je leur dis "mais oui, c'est encore plus facile qu'on ne croit puisqu'on la connaît déjà un peu, cette règle !", tout en concluant par "concernant les relatifs, vous avez fait le plus dur avec les additions et soustractions, vous allez voir que le reste est plus simple".
J'interroge ensuite pas mal d'élèves (surtout ceux qui se faisaient oublier ou regardaient plus mes pieds que le tableau ) sur des calculs ultra basique genre 6x(-2), (-9)x(-10) etc... pour les forcer à cogiter dès le début à bien appliquer la règle (pourtant ultra simple, mais j'ai des paresseux qui ont besoin qu'on aille les chercher)... Et hop on note la règle dans la leçon (avec encore des exemples et encore des élèves interrogés) puis exos d'applications à la pelle.
) sur des calculs ultra basique genre 6x(-2), (-9)x(-10) etc... pour les forcer à cogiter dès le début à bien appliquer la règle (pourtant ultra simple, mais j'ai des paresseux qui ont besoin qu'on aille les chercher)... Et hop on note la règle dans la leçon (avec encore des exemples et encore des élèves interrogés) puis exos d'applications à la pelle. 
Au tableau, je leur demande comment ils ont appris à faire 5x3 quand ils étaient petits (ça les fait sourire de fouiller dans leurs souvenirs). Ils vont me dire par exemple 5+5+5, et le résultat. Je note les calculs en même temps.
Sur une autre ligne, je leur dis "eh bien on va s'en servir pour essayer de deviner le résultat de (-5)x3". (si jamais ils avaient proposé 3+3+3+3+3, je leur demande plutôt 5x(-3), du coup). On écrit donc (-5)x3 = (-5)+(-5)+(-5) = -15.
Et si c'était 4x(-3) ? Ils proposent assez spontanément de faire une somme de facteurs (-3).
Mais alors si on a (-4)x(-8) ? Certains vont proposer -32, d'autres 32, d'autres on ne peut pas savoir... Comme ils ne sont pas d'accord, je leur propose d'écrire la table du (-8) et de la poursuivre :
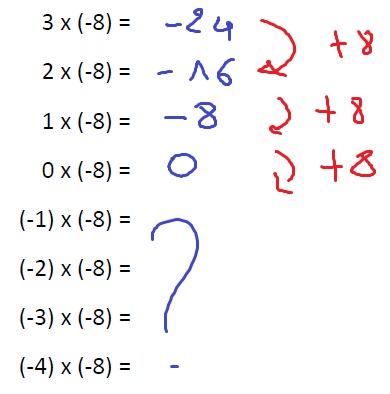
on trouve les résultats en bleu facilement puisqu'on vient de comprendre comment ça marchait quand on multipliait un positif par un négatif. Puis je leur demande de trouver une logique pour passer d'un résultat au suivant, on me dit qu'on enlève 8 (y en a toujours pour se planter), mais on remarque assez vite qu'en fait on ajoute 8 (par exemple -24 + 8 = -16), et donc j'ajoute les opérateurs en rouge sur le côté. Et on prolonge le raisonnement du côté des facteurs négatifs, et ooooh, ils sont tout contents de remarquer que le résultat est en fait tout simple à trouver. On résume tout de suite schématiquement au tableau avec :
(+)x(+) -> +
(-)x(-) -> +
(+)x(-) -> -
(-)x(+) -> -
et là il y en a toujours un pour avoir un éclair de lucidité et me lancer spontanément "oh mais c'est la même règle des signes que quand on retire les parenthèses !!" (ou sinon je leur tends un peu la perche
 ), et là je leur dis "mais oui, c'est encore plus facile qu'on ne croit puisqu'on la connaît déjà un peu, cette règle !", tout en concluant par "concernant les relatifs, vous avez fait le plus dur avec les additions et soustractions, vous allez voir que le reste est plus simple".
), et là je leur dis "mais oui, c'est encore plus facile qu'on ne croit puisqu'on la connaît déjà un peu, cette règle !", tout en concluant par "concernant les relatifs, vous avez fait le plus dur avec les additions et soustractions, vous allez voir que le reste est plus simple".J'interroge ensuite pas mal d'élèves (surtout ceux qui se faisaient oublier ou regardaient plus mes pieds que le tableau

 gmsl65.Niveau 2
gmsl65.Niveau 2
Bonjour,
Merci beaucoup X.Y.U. pour ce partage, votre façon de procéder est simple et pertinente !
Je pense que c'est plus adapté à des collégiens que de passer par la simple distributivité.
C'est bien plus simple et je pense que ça les accrochera davantage.
Merci beaucoup X.Y.U. pour ce partage, votre façon de procéder est simple et pertinente !
Je pense que c'est plus adapté à des collégiens que de passer par la simple distributivité.
C'est bien plus simple et je pense que ça les accrochera davantage.
 Manu7Expert spécialisé
Manu7Expert spécialisé
Cette découverte est intéressante, mais je ne suis pas certain que cela soit une preuve. J'ai l'impression que pour justifier cet ordre il faut déjà savoir que (-1) x (-8) est inférieur à 0 x (-8) et je me demande comment on le prouve ? Il faudrait pour cela définir la multiplication par (-1) et c'est justement le but de cette démonstration. Après tout comme les signes changent on pourrait bien dire que la logique serait de faire -8 maintenant. Je vois bien la logique tant qu'on multiplie par un facteur positif mais une quantité négative de facteurs on ne sait pas trop ce que cela signifie, donc pour moi c'est davantage une conjecture qu'une preuve.
Après cette présentation est intéressante, mais nous ne sommes pas obligés de tout démontrer, c'est vrai que j'aime bien passer par la distributivité car c'est l'occasion de la retravailler mais au final nous sommes d'accord que cette preuve n'est pas essentielle pour aider à retenir. A la limite, on peut se souvenir que c'est prouvé et on oublie très vite cette démonstration. J'aime bien rapidement passer à une grille de multiplication où on retrouve ce même phénomène d'ordre et on découvre aussi les 4 quadrants qui illustre très bien les règles des signes.
Après cette présentation est intéressante, mais nous ne sommes pas obligés de tout démontrer, c'est vrai que j'aime bien passer par la distributivité car c'est l'occasion de la retravailler mais au final nous sommes d'accord que cette preuve n'est pas essentielle pour aider à retenir. A la limite, on peut se souvenir que c'est prouvé et on oublie très vite cette démonstration. J'aime bien rapidement passer à une grille de multiplication où on retrouve ce même phénomène d'ordre et on découvre aussi les 4 quadrants qui illustre très bien les règles des signes.
 MathadorEmpereur
MathadorEmpereur
Comment voudrais-tu « prouver » que -1×(-8)=8 alors que la multiplication n'est pas encore définie sur Z² ?Manu7 a écrit:Cette découverte est intéressante, mais je ne suis pas certain que cela soit une preuve. J'ai l'impression que pour justifier cet ordre il faut déjà savoir que (-1) x (-8) est inférieur à 0 x (-8) et je me demande comment on le prouve ? Il faudrait pour cela définir la multiplication par (-1) et c'est justement le but de cette démonstration. Après tout comme les signes changent on pourrait bien dire que la logique serait de faire -8 maintenant. Je vois bien la logique tant qu'on multiplie par un facteur positif mais une quantité négative de facteurs on ne sait pas trop ce que cela signifie, donc pour moi c'est davantage une conjecture qu'une preuve.
On pourrait tout à fait la prolonger en décidant que -1×(-8)=-8, c'est juste qu'on perdrait beaucoup des sympathiques propriétés opératoires auxquelles on est habitués.
Parfois on l'accepte (pour les quaternions et la commutativité par exemple) mais en général on l'évite.
La seule chose qu'on pourrait démontrer est donc un énoncé du type « Tout anneau (commutatif, pour simplifier la démonstration) vérifie la règle des signes. », sachant que Z et Q sont justement les premiers anneaux qu'ils rencontrent…
_________________
"There are three kinds of lies: lies, damned lies, and statistics." (cité par Mark Twain)
« Vulnerasti cor meum, soror mea, sponsa; vulnerasti cor meum in uno oculorum tuorum, et in uno crine colli tui.
Quam pulchrae sunt mammae tuae, soror mea sponsa! pulchriora sunt ubera tua vino, et odor unguentorum tuorum super omnia aromata. » (Canticum Canticorum 4:9-10)
 Manu7Expert spécialisé
Manu7Expert spécialisé
Je suis d'accord, on ne peut pas vraiment démontrer cette règle c'est plutôt une définition qui nous arrange bien au niveau des propriétés opératoires.
 X.Y.U.Niveau 7
X.Y.U.Niveau 7
Vu ce que les programmes sont devenus, j'avoue que j'ai beaucoup baissé mon niveau d'exigence quant aux démonstrations des propriétés vues en classe, et le but n'est plus pour moi d'être exhaustive mais plutôt convaincante et assez rapide, je préfère qu'ils consacrent du temps aux applications, j'ai d'ailleurs laissé tomber beaucoup d' "activités de découvertes" où l'élève construit son savoir tout seul (en théorie...). Le temps manque et les élèves sont de plus en plus lents globalement...
@gmsl65. : de rien , contente d'avoir pu t'aider.
, contente d'avoir pu t'aider.
@gmsl65. : de rien
 , contente d'avoir pu t'aider.
, contente d'avoir pu t'aider.Permission de ce forum:
Vous ne pouvez pas répondre aux sujets dans ce forum




