 gmsl65.Niveau 2
gmsl65.Niveau 2
Bonjour,
En quatrième, dans le chapitre "Proportionnalité", on donne la propriété des produits en croix.
Je sais qu'au collège, on ne donne quasiment aucune "preuve formelle" dans un cours.
Je me pose la question de la justification en amont de cette propriété.
Je me disais que je pourrais leur donner un tableau de proportionnalité; par exemple 3 et 6 en ligne et 5,4 et 12,6 en colonne.
Puis leur demander de justifier que c'est un tableau de proportionnalité. Une des méthodes vues en 6ème et 5ème est le coefficient de proportionnalité. On arriverait donc à 5,4/3=12,6/7. A partir de là, j'utiliserai l'idée "on ne change pas une égalité en multipliant chaque membre par un même nombre" même si cette propriété n'a pas été formalisée dans un cours et j'écrirai donc 5,4/3*3*7=12,6/7*7*3.
J'utiliserai ensuite la formule a/b*b=a qu'ils connaissent normalement depuis la 6ème... Pour avoir 5,4*7=12,6*3 (puisque 5,4/3*3=5,4 et
12,6/7*7=12,6). J'obtiendrais alors l'égalité des produits en croix. Je ferais ça dans une activité d'introduction. Dans le cours, j'énoncerai la propriété sans la démontrer, en l'appliquant simplement sur un exemple.
Comment faîtes-vous dans vos cours ?
Autre chose qui me dérange. J'ai pu voir écrit ceci "Dans un tableau de proportionnalité ..., on a l'égalité a*d=b*c". Il manque la réciproque... Je rajouterai (Réciproquement, si a*d=b*c alors le tableau ... est un tableau de proportionnalité".
Je trouve que c'est important que soit écrit la réciproque car en pratique on peut être amené à utiliser cette propriété dans les deux sens.
Merci par avance pour vos remarques et commentaires.
En quatrième, dans le chapitre "Proportionnalité", on donne la propriété des produits en croix.
Je sais qu'au collège, on ne donne quasiment aucune "preuve formelle" dans un cours.
Je me pose la question de la justification en amont de cette propriété.
Je me disais que je pourrais leur donner un tableau de proportionnalité; par exemple 3 et 6 en ligne et 5,4 et 12,6 en colonne.
Puis leur demander de justifier que c'est un tableau de proportionnalité. Une des méthodes vues en 6ème et 5ème est le coefficient de proportionnalité. On arriverait donc à 5,4/3=12,6/7. A partir de là, j'utiliserai l'idée "on ne change pas une égalité en multipliant chaque membre par un même nombre" même si cette propriété n'a pas été formalisée dans un cours et j'écrirai donc 5,4/3*3*7=12,6/7*7*3.
J'utiliserai ensuite la formule a/b*b=a qu'ils connaissent normalement depuis la 6ème... Pour avoir 5,4*7=12,6*3 (puisque 5,4/3*3=5,4 et
12,6/7*7=12,6). J'obtiendrais alors l'égalité des produits en croix. Je ferais ça dans une activité d'introduction. Dans le cours, j'énoncerai la propriété sans la démontrer, en l'appliquant simplement sur un exemple.
Comment faîtes-vous dans vos cours ?
Autre chose qui me dérange. J'ai pu voir écrit ceci "Dans un tableau de proportionnalité ..., on a l'égalité a*d=b*c". Il manque la réciproque... Je rajouterai (Réciproquement, si a*d=b*c alors le tableau ... est un tableau de proportionnalité".
Je trouve que c'est important que soit écrit la réciproque car en pratique on peut être amené à utiliser cette propriété dans les deux sens.
Merci par avance pour vos remarques et commentaires.
 X.Y.U.Niveau 7
X.Y.U.Niveau 7
Bonjour,
Concernant la preuve du produit en croix (dans le sens direct, donc), je le fais chaque année avec mes 4ème, rapidement au tableau (ils ne notent pas, je préfère qu'ils soient bien attentifs), mais je trouve dommage de le faire sur un cas particulier avec des nombres, autant le faire directement avec les lettres. Grosso modo je procède ainsi : on imagine un tableau 2x2 de proportionnalité, et on en déduit que les quotients de chaque colonne sont égaux (puisqu'il s'agit du coef de proportionnalité). [je ne mets pas de "flèche" d'implication, et je vais à la ligne à chaque fois. Puis on multiplie chaque membre de l'égalité par le même nombre c (bon, là, je perds déjà quelques élèves), et on "simplifie" (le chapitre des fractions est déjà passé plus tôt dans l'année) (je perds encore qq élèves qui ne voient pas trop pourquoi on fait ça). Enfin on multiplie par un même nombre d et on simplifie (j'en perds encore qq uns). On obtient l'égalité des produits en croix. Et je rajoute ensuite les doubles flèches dans le tableau pour bien voir les produits "en diagonale". Et je rassure tout ce petit monde qu'ils n'ont pas à retenir cette démonstration mais simplement les données et la conclusion.
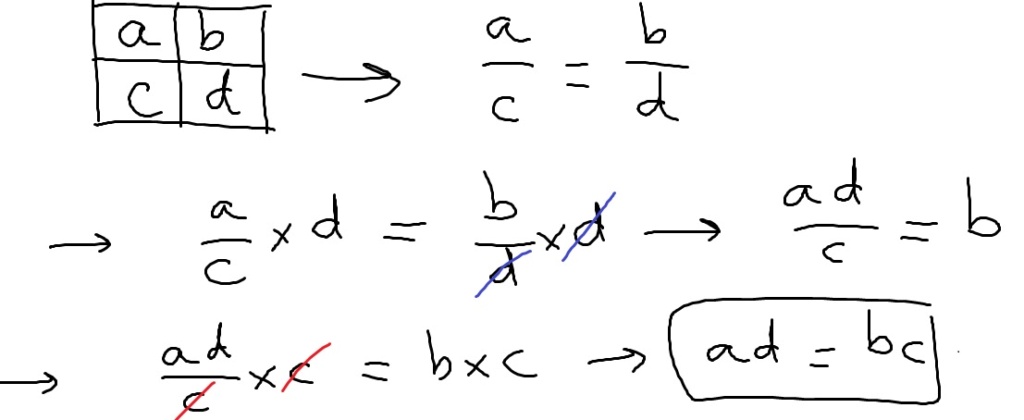
Comme toi, on écrit dans la leçon les deux propriétés (directe et réciproque) même si on utilise beaucoup plus la directe...
Concernant la preuve du produit en croix (dans le sens direct, donc), je le fais chaque année avec mes 4ème, rapidement au tableau (ils ne notent pas, je préfère qu'ils soient bien attentifs), mais je trouve dommage de le faire sur un cas particulier avec des nombres, autant le faire directement avec les lettres. Grosso modo je procède ainsi : on imagine un tableau 2x2 de proportionnalité, et on en déduit que les quotients de chaque colonne sont égaux (puisqu'il s'agit du coef de proportionnalité). [je ne mets pas de "flèche" d'implication, et je vais à la ligne à chaque fois. Puis on multiplie chaque membre de l'égalité par le même nombre c (bon, là, je perds déjà quelques élèves), et on "simplifie" (le chapitre des fractions est déjà passé plus tôt dans l'année) (je perds encore qq élèves qui ne voient pas trop pourquoi on fait ça). Enfin on multiplie par un même nombre d et on simplifie (j'en perds encore qq uns). On obtient l'égalité des produits en croix. Et je rajoute ensuite les doubles flèches dans le tableau pour bien voir les produits "en diagonale". Et je rassure tout ce petit monde qu'ils n'ont pas à retenir cette démonstration mais simplement les données et la conclusion.
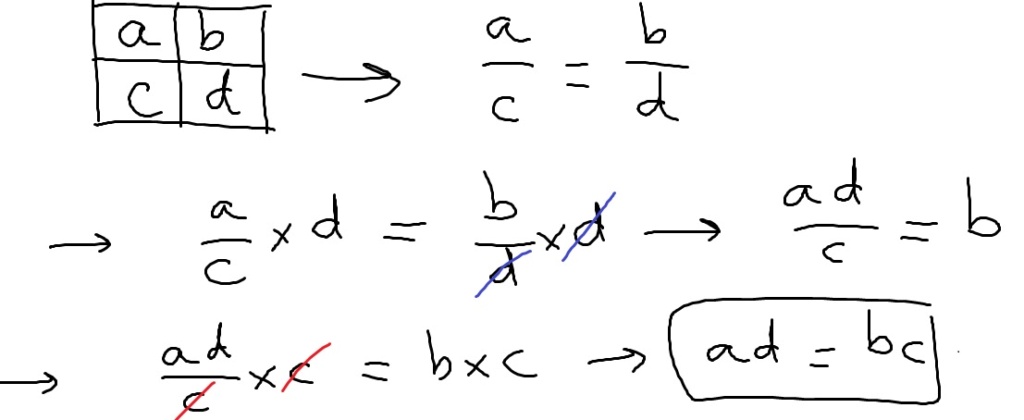
Comme toi, on écrit dans la leçon les deux propriétés (directe et réciproque) même si on utilise beaucoup plus la directe...
 ProtonExpert
ProtonExpert
Pourquoi ne pas les mettre sur dc au dénominateur pour avoir l’égalité des produits en croix ?
Réciproquement tu fais la différence entre les deux fractions.
Réciproquement tu fais la différence entre les deux fractions.
 X.Y.U.Niveau 7
X.Y.U.Niveau 7
Ah mais oui, en plus je crois que j'avais plutôt fait comme ça l'an dernier, tu as raison !  Surtout qu'on avait fait les transformations au même dénominateur assez récemment... ;-) Merci pour ta remarque !
Surtout qu'on avait fait les transformations au même dénominateur assez récemment... ;-) Merci pour ta remarque !
 Surtout qu'on avait fait les transformations au même dénominateur assez récemment... ;-) Merci pour ta remarque !
Surtout qu'on avait fait les transformations au même dénominateur assez récemment... ;-) Merci pour ta remarque !Permission de ce forum:
Vous ne pouvez pas répondre aux sujets dans ce forum




