passer une porte d'un couloir à un autre : sujet de géométrie d'un triangle rectangle

Deux couloirs de largeur a et b sont à angles droits. Quelle la longueur maximum d'une porte peut-on faire passer d'un couloir à un autre ?
C'est un sujet donné il y a 30 ans en bac technique.
Cela peut se traduire ainsi :Soient 2 demi-droites orthogonales d et d' et un point A situé dans leur quart de plan. Quelle est la longueur minimale de l'hypoténuse d'un triangle passant par A, B et C  où A est sur l'hypoténuse, B est sur d et C est sur d' ?  
Je l'ai résolu de manière analytique et on trouve une jolie formule avec des racines carrées et des racines cubiques.
Mais y a t-il une manière géométrique ?

S'il y a des racines cubiques dans la formule, cela veut dire que le nombre n'est probablement pas constructible à la règle et au compas à partir des données de départ.
Je penche donc plutôt vers un non.

Si l'on paramètre le triangle ABC à partir des coordonnées de A =(x,0), en prenant B=(0,0) et C=(0,..), et que l'on regarde AC^2, on obtient la fonction f(x)= x^2+(ax/(x-b))^2 dont la dérivée s'annule en c=(a^2b)^(1/3)+b.

Cette quantité est en général impossible à construire à la règle et au compas en effet.

Après simplification on a AC^2= (a^(2/3)+b^(2/3))^3.

En prenant a=1, on a (1+b^(2/3))^3.

Ce nombre n'est pas non plus constructible à la règle et au compas en général.
Pour b=2, en posant y=2^(2/3), construire AC^2 revient à construire y+y^2.
On trouve que y+y^2 est une racine du polynôme X^3-12X-20 (on élève au cube et on remarque que y^3=4).
Ce polynôme n'a pas de racines rationnelles, donc il est irréductible de degré 3 sur Q. Ce qui montre que AC^2 n'est pas constructible à la règle et au compas.

Tina08 a écrit:Deux couloirs de largeur a et b sont à angles droits. Quelle la longueur maximum d'une porte peut-on faire passer d'un couloir à un autre ?
C'est un sujet donné il y a 30 ans en bac technique.

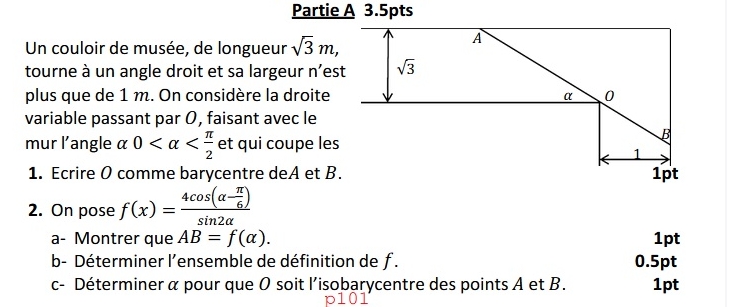
J'ai en tête cette figure ( effectivement bac F dans les années 80-mes débuts dans l'enseignement ) avec un énoncé légèrement différent : Un tableau pas une porte et une étude de fonction.

On m'a dit en effet que c'était le sujet du bac F1  construction mécanique de 1984 pour l'académie de Nancy-Metz. C'est un ancien élève frustré de n'avoir pas pu faire cet exercice à l'époque qui me l'a donné oralement. J'ai pu enfin le soulager après toutes ces années ! Toutefois, je ne pense pas que le sujet à l'époque était donné comme je l'ai écrit. Il devait être plus guidé comme le tien mais les souvenirs s'estompent...
Je pense que la suite de ton sujet consistait à chercher le minimum de la fonction f.

lisa81 a écrit:
J'ai en tête cette figure ( effectivement bac F dans les années 80-mes débuts dans l'enseignement ) avec un énoncé légèrement différent : Un tableau pas une porte et une étude de fonction.

Bac F dans les années 80. Imaginez les dégats si on posait ça au CAPES aujourd'hui.

(Bon, les programmes ont évolué et les élèves sont moins entraînés à ce genre de problème, c'est sûr. Cela dit, si le changement revient à mettre de la pseudo-algorithmique ou des probas nunuches à la place...)

Je suis d'accord avec toi, Prezbo. Je suis nostalgique des maths qui permettaient d'entrer dans un magnifique univers.. Quand je dis que je cherchais une autre manière de faire, je cherchais comment éviter de passer par la dérivée. Bien sûr, une racine cubique n'est pas constructible à la règle et au compas

Un article du Mathematics Magazine à ce sujet, traitant notamment de l'apparition de l'équation de l'astroïde dans ce problème.

Solving the Ladder Problem on the Back of an Envelope
Dan Kalman
Mathematics Magazine
Vol. 80, No. 3 (Jun., 2007)

Lien : dankalman POINT net SLASH preprints SLASH ladder_paper_MM.pdf (je n'ai pas encore le droit de poster de lien)

J'ai essayé de résoudre ce problème concrètement au cours d'un déménagement avec une table ... heureusement j'ai pu démontrer l'impossibilité mathématique de l'introduction de le table dans la pièce au bout du couloir ...

J'aime beaucoup l'approche de Dan Kalman qui est très belle ! Merci mnmnm !
Voltaire, en pratique, on peut quelquefois mettre la table debout ! ou prendre un mètre. Ce problème n'a de sens que pour s'amuser.