Page 4 sur 4 •  1, 2, 3, 4
1, 2, 3, 4
 1, 2, 3, 4
1, 2, 3, 4- LaverdureEmpereur
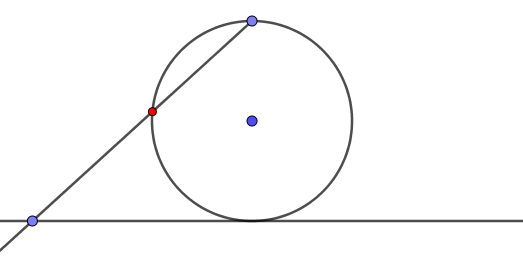
JPhMM a écrit:Tu as oublié le point à l'infini.William Foster a écrit:Tu prends un cercle, une droite qui lui est tangente en B, et le point A (en haut sur le dessin) du cercle diamétralement opposé à B.AndréC a écrit:Je ne connais pas cette démonstration.
Si maintenant tu prends un point M sur la droite et que tu traces [AM), cette demi-droite coupe le cercle en un seul point N (en rouge sur le dessin). A tout point M correspond un et un seul point N.
Inversement, pour tout point N du cercle, la demi-droite [AN) coupe la droite en un seul point M.
Tout point M est pote avec un seul point N. Tout point N est pote avec un seul point M. Il y a donc autant de points sur la droite que sur le cercle...
...
...
Oui mais non : le point A est le seul à ne pas avoir d'ami sur la droite. Le cercle possède donc un point (le A) de plus que la droite !
Edit : merci de ne pas éreinter la forme de mon explication que j'ai tentée de faire compréhensible aux profanes

Je viens de regarder ça sur internet et justement je me demande, si on considère le point à l'infini (si j'ai bien compris, ça revient à faire bouger le point M vers la gauche donc rendre les droite (AM) et la tangente progressivement "parallèles") est-ce qu'on peut dire que "A sera pote avec M" (
 JPhMMDemi-dieu
JPhMMDemi-dieu
Et une droite compactifiée, une !William Foster a écrit:Bouge pas, je vais le chercher...JPhMM a écrit:
Tu as oublié le point à l'infini.

_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
 JPhMMDemi-dieu
JPhMMDemi-dieu
Voilà.Laverdure a écrit:JPhMM a écrit:Tu as oublié le point à l'infini.William Foster a écrit:Tu prends un cercle, une droite qui lui est tangente en B, et le point A (en haut sur le dessin) du cercle diamétralement opposé à B.AndréC a écrit:Je ne connais pas cette démonstration.
Si maintenant tu prends un point M sur la droite et que tu traces [AM), cette demi-droite coupe le cercle en un seul point N (en rouge sur le dessin). A tout point M correspond un et un seul point N.
Inversement, pour tout point N du cercle, la demi-droite [AN) coupe la droite en un seul point M.
Tout point M est pote avec un seul point N. Tout point N est pote avec un seul point M. Il y a donc autant de points sur la droite que sur le cercle...
...
...
Oui mais non : le point A est le seul à ne pas avoir d'ami sur la droite. Le cercle possède donc un point (le A) de plus que la droite !
Edit : merci de ne pas éreinter la forme de mon explication que j'ai tentée de faire compréhensible aux profanes

Je viens de regarder ça sur internet et justement je me demande, si on considère le point à l'infini (si j'ai bien compris, ça revient à faire bouger le point M vers la gauche donc rendre les droite (AM) et la tangente progressivement "parallèles") est-ce qu'on peut dire que "A sera pote avec M" () ? J'ai l'impression qu'alors, A et N se confondraient.
Le compactifié d'Alexandrov de IR (c'est-à-dire la droite IR plus le point à l'infini) est homéomorphe à un cercle.
La question qui tue : pourquoi le point à l'infini, et pas les 2 points à l'infini ? vous avez 2 heures.
- Spoiler:
- Précisément par que la droite compactifiée est homéomorphe à un cercle, donc elle se "referme" à l'infini, comme un cercle.

_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
 William FosterExpert
William FosterExpert
Mais si tu vas chercher le point à l'infini à gauche, tu vas oublier celui de droite...Laverdure a écrit:Je viens de regarder ça sur internet et justement je me demande, si on considère le point à l'infini (si j'ai bien compris, ça revient à faire bouger le point M vers la gauche donc rendre les droite (AM) et la tangente progressivement "parallèles") est-ce qu'on peut dire que "A sera pote avec M" () ? J'ai l'impression qu'alors, A et N se confondraient.
Ou alors ça voudrait dire que A qui est au sommet correspond à "infiniment à gauche" ET "infiniment à droite", ce qui impliquerait de faire passer le fil en restreint car trop proche de la politique jupitérienne.
_________________
Tout le monde me dit que je ne peux pas faire l'unanimité.
"Opinions are like orgasms : mine matters most and I really don't care if you have one." Sylvia Plath
Vérificateur de miroir est un métier que je me verrais bien faire, un jour.
 JPhMMDemi-dieu
JPhMMDemi-dieu
Pour vous détendre, un petit film.
Aller à partir de 7 min pour rejoindre ce qui nous concerne.
Aller à partir de 7 min pour rejoindre ce qui nous concerne.
_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
 BrindIfFidèle du forum
BrindIfFidèle du forum
Je regarde les chapitres sur les complexes avec mes élèves de 1re.
 LaverdureEmpereur
LaverdureEmpereur
William Foster a écrit:Mais si tu vas chercher le point à l'infini à gauche, tu vas oublier celui de droite...Laverdure a écrit:Je viens de regarder ça sur internet et justement je me demande, si on considère le point à l'infini (si j'ai bien compris, ça revient à faire bouger le point M vers la gauche donc rendre les droite (AM) et la tangente progressivement "parallèles") est-ce qu'on peut dire que "A sera pote avec M" () ? J'ai l'impression qu'alors, A et N se confondraient.
Ou alors ça voudrait dire que A qui est au sommet correspond à "infiniment à gauche" ET "infiniment à droite", ce qui impliquerait de faire passer le fil en restreint car trop proche de la politique jupitérienne.
:lol:
Du coup, j'ai une autre question : quand on prend le point M qui se trouve "à l'endroit" du point B, est-ce qu'on peut pas dire, alors, que "A a un pote" en quelque sorte ? Dans ce cas, on aurait [AN) qui couperait la droite tangente en un seul point, B qui se confondrait avec le point M et avec le point N, non ?
EDIT : c'est plus clair avec ta remarque sur le point infini de droite oublié (le pauvre) mais le cas du point B me pose encore problème.
_________________

 JPhMMDemi-dieu
JPhMMDemi-dieu
Sauf à considérer la droite comme un cercle de rayon infini.William Foster a écrit:Mais si tu vas chercher le point à l'infini à gauche, tu vas oublier celui de droite...Laverdure a écrit:Je viens de regarder ça sur internet et justement je me demande, si on considère le point à l'infini (si j'ai bien compris, ça revient à faire bouger le point M vers la gauche donc rendre les droite (AM) et la tangente progressivement "parallèles") est-ce qu'on peut dire que "A sera pote avec M" () ? J'ai l'impression qu'alors, A et N se confondraient.
Ou alors ça voudrait dire que A qui est au sommet correspond à "infiniment à gauche" ET "infiniment à droite", ce qui impliquerait de faire passer le fil en restreint car trop proche de la politique jupitérienne.

_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
 William FosterExpert
William FosterExpert
Oué bah bon courage pour trouver un compas aussi grand !JPhMM a écrit:Sauf à considérer la droite comme un cercle de rayon infini.William Foster a écrit:Mais si tu vas chercher le point à l'infini à gauche, tu vas oublier celui de droite...Laverdure a écrit:Je viens de regarder ça sur internet et justement je me demande, si on considère le point à l'infini (si j'ai bien compris, ça revient à faire bouger le point M vers la gauche donc rendre les droite (AM) et la tangente progressivement "parallèles") est-ce qu'on peut dire que "A sera pote avec M" () ? J'ai l'impression qu'alors, A et N se confondraient.
Ou alors ça voudrait dire que A qui est au sommet correspond à "infiniment à gauche" ET "infiniment à droite", ce qui impliquerait de faire passer le fil en restreint car trop proche de la politique jupitérienne.

_________________
Tout le monde me dit que je ne peux pas faire l'unanimité.
"Opinions are like orgasms : mine matters most and I really don't care if you have one." Sylvia Plath
Vérificateur de miroir est un métier que je me verrais bien faire, un jour.
 JPhMMDemi-dieu
JPhMMDemi-dieu
La droite est tangente au cercle en B. Donc le pote de B est B.Laverdure a écrit:William Foster a écrit:Mais si tu vas chercher le point à l'infini à gauche, tu vas oublier celui de droite...Laverdure a écrit:Je viens de regarder ça sur internet et justement je me demande, si on considère le point à l'infini (si j'ai bien compris, ça revient à faire bouger le point M vers la gauche donc rendre les droite (AM) et la tangente progressivement "parallèles") est-ce qu'on peut dire que "A sera pote avec M" () ? J'ai l'impression qu'alors, A et N se confondraient.
Ou alors ça voudrait dire que A qui est au sommet correspond à "infiniment à gauche" ET "infiniment à droite", ce qui impliquerait de faire passer le fil en restreint car trop proche de la politique jupitérienne.
:lol:
Du coup, j'ai une autre question : quand on prend le point M qui se trouve "à l'endroit" du point B, est-ce qu'on peut pas dire, alors, que "A a un pote" en quelque sorte ? Dans ce cas, on aurait [AN) qui couperait la droite tangente en un seul point, B qui se confondrait avec le point M et avec le point N, non ?
EDIT : c'est plus clair avec ta remarque sur le point infini de droite oublié (le pauvre) mais le cas du point B me pose encore problème.
_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
 LaverdureEmpereur
LaverdureEmpereur
Ah ben oui, bien sûr : en reprenant mon schéma, c'est clair 
_________________

 JPhMMDemi-dieu
JPhMMDemi-dieu
Y'a moyen de s'amuser à transformer les cercles en droites sous Geogebra.William Foster a écrit:Oué bah bon courage pour trouver un compas aussi grand !JPhMM a écrit:Sauf à considérer la droite comme un cercle de rayon infini.William Foster a écrit:Mais si tu vas chercher le point à l'infini à gauche, tu vas oublier celui de droite...Laverdure a écrit:Je viens de regarder ça sur internet et justement je me demande, si on considère le point à l'infini (si j'ai bien compris, ça revient à faire bouger le point M vers la gauche donc rendre les droite (AM) et la tangente progressivement "parallèles") est-ce qu'on peut dire que "A sera pote avec M" () ? J'ai l'impression qu'alors, A et N se confondraient.
Ou alors ça voudrait dire que A qui est au sommet correspond à "infiniment à gauche" ET "infiniment à droite", ce qui impliquerait de faire passer le fil en restreint car trop proche de la politique jupitérienne.

Il suffit de tracer le cercle circonscrit à un triangle et de dégénérer le triangle.
Enjoy !
Z'ont des jeux cons ces profs de maths !

_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
Page 4 sur 4 •  1, 2, 3, 4
1, 2, 3, 4
 1, 2, 3, 4
1, 2, 3, 4- E. Lévinas, Totalité et Infini (notes de lecture)
- 31.01 / 01.02 2012 : Grand Colloque lettres classiques "Refonder l'enseignement du latin et du grec" (lycée Louis le Grand)
- Agota Kristof, Le Grand Cahier, Grand-Mère
- science étonnante #24 - l'infini
- Désir d'infini : des chiffres, des univers et des hommes
Permission de ce forum:
Vous ne pouvez pas répondre aux sujets dans ce forum