Page 3 sur 4 •  1, 2, 3, 4
1, 2, 3, 4 
 1, 2, 3, 4
1, 2, 3, 4 
- JPhMMDemi-dieu
Fort naïvement : si l'infini (ici l'ensemble N donc) n'existait pas, les paradoxes de Zénon ne nous poseraient-ils pas un très sérieux problème ?
 William FosterExpert
William FosterExpert
Bah même avec l'infini ils me posent encore problème, personnellement...JPhMM a écrit:Fort naïvement : si l'infini (ici l'ensemble N donc) n'existait pas, les paradoxes de Zénon ne nous poseraient-ils pas un très sérieux problème ?
Que d'un seul trait continu on puisse atteindre l'infini me laisse encore coi de temps à autres. Un peu comme la fonction de Peano évoquée plus haut dans le fil. C'est le genre de raisonnement que je trouve hypnotique et sur lequel je peux rester éberlué des heures.
_________________
Tout le monde me dit que je ne peux pas faire l'unanimité.
"Opinions are like orgasms : mine matters most and I really don't care if you have one." Sylvia Plath
Vérificateur de miroir est un métier que je me verrais bien faire, un jour.
 JPhMMDemi-dieu
JPhMMDemi-dieu
Je le comprends aisément, puisque je partage cette impression. 
(Je bloque un peu sur l'idée qu'Achille arrive à rattraper la tortue. Cette histoire selon laquelle 1/2 + 1/4 + 1/8 + ... atteindrait 1, extrémité de l'intervalle fermé [0;1] me gratouillera toujours un peu aux entournures. Topologiquement, ça a un côté urtiquant, je trouve.)

(Je bloque un peu sur l'idée qu'Achille arrive à rattraper la tortue. Cette histoire selon laquelle 1/2 + 1/4 + 1/8 + ... atteindrait 1, extrémité de l'intervalle fermé [0;1] me gratouillera toujours un peu aux entournures. Topologiquement, ça a un côté urtiquant, je trouve.)
_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
 SirgabNiveau 4
SirgabNiveau 4
Les paradoxes de Zénon sont liés à la confusion entre l'infini en puissance et l'infini en acte. En suivant Aristote, on peut dire que l'infini n'existe pas en acte, mais seulement en puissance. Le continu est divisible à l'infini, mais pour autant il n'est pas divisé à l'infini. En traçant une ligne, je ne trace pas une infinité de points, mais je fais apparaître une divisibilité infinie dans le continu.
 User17706Bon génie
User17706Bon génie
Le problème étant de savoir s'il est possible de suivre Aristote, justement. Tiens, au nombre des heureuses (et heureusement nombreuses) exceptions dont je parlais tout à l'heure, il y a, de Jean-Louis Gardies, Pascal entre Eudoxe et Cantor chez Vrin.
 SirgabNiveau 4
SirgabNiveau 4
Je vais commencer par l'ouvrage recommandé plus haut. Mais celui-ci a l'air aussi rudement intéressant.
Je me demande si Husserl ne s'est pas intéressé aussi de près à ces questions, étant mathématicien de formation.
Je me demande si Husserl ne s'est pas intéressé aussi de près à ces questions, étant mathématicien de formation.
 BalthazaardVénérable
BalthazaardVénérable
JPhMM a écrit:Je le comprends aisément, puisque je partage cette impression.
(Je bloque un peu sur l'idée qu'Achille arrive à rattraper la tortue. Cette histoire selon laquelle 1/2 + 1/4 + 1/8 + ... atteindrait 1, extrémité de l'intervalle fermé [0;1] me gratouillera toujours un peu aux entournures. Topologiquement, ça a un côté urtiquant, je trouve.)
Moi aussi, l'argument à base de convergence a du mal à me convaincre entièrement.
 jaybeNiveau 9
jaybeNiveau 9
Un joli paradoxe qui semble difficile à trouver en français, en voici une version probablement un peu différente de celle originelle : paradoxe de Benardete (certains auteurs l'ont qualifié de "new Zeno paradox").
Un homme veut se rendre d'une ville A à une ville B.
Sur sa route, une infinité dénombrable de démons veut l'empêcher d'atteindre la ville B.
Pour tout n entier naturel, le démon n décide que lorsque l'homme aura parcouru 1/2^(n+1) du chemin, il dressera aussitôt devant lui un mur infranchissable (le démon 0 décide que lorsque l'homme aura parcouru la moitié du chemin, il dressera aussitôt devant lui un mur infranchissable ; le démon 1 décide que lorsque l'homme aura parcouru le quart du chemin, il dressera aussitôt devant lui un mur infranchissable, etc.).
Si le démon n fabrique le mur qui bloque l'homme, cela implique que le démon n+1 n'a pas fait son boulot, donc aucun démon ne construit de mur et l'homme atteint la ville B.
Un homme veut se rendre d'une ville A à une ville B.
Sur sa route, une infinité dénombrable de démons veut l'empêcher d'atteindre la ville B.
Pour tout n entier naturel, le démon n décide que lorsque l'homme aura parcouru 1/2^(n+1) du chemin, il dressera aussitôt devant lui un mur infranchissable (le démon 0 décide que lorsque l'homme aura parcouru la moitié du chemin, il dressera aussitôt devant lui un mur infranchissable ; le démon 1 décide que lorsque l'homme aura parcouru le quart du chemin, il dressera aussitôt devant lui un mur infranchissable, etc.).
Si le démon n fabrique le mur qui bloque l'homme, cela implique que le démon n+1 n'a pas fait son boulot, donc aucun démon ne construit de mur et l'homme atteint la ville B.
_________________
Les mathématiciens ne sont pas des gens qui trouvent les mathématiques faciles ; comme tout le monde, ils savent qu'elles sont difficiles, mais ça ne leur fait pas peur !
 William FosterExpert
William FosterExpert
On dirait un peu le paradoxe du prisonnier en version "infini".
_________________
Tout le monde me dit que je ne peux pas faire l'unanimité.
"Opinions are like orgasms : mine matters most and I really don't care if you have one." Sylvia Plath
Vérificateur de miroir est un métier que je me verrais bien faire, un jour.
 PrezboGrand Maître
PrezboGrand Maître
PauvreYorick a écrit:C'est peut-être moi qui comprends mal l'axiome de l'infini. Mais très grossièrement j'y vois une façon de postuler que N, ou un ensemble similaire, existe.
Ah oui, l'existence de N est bien une conséquence de l'axiome de l'infini. C'est amusant, effectivement, puisqu'on à une infinité de cardinaux infinis...A condition d'admettre qu'on en a au moins un.
En fait, je suis comme la plupart des matheux : je me suis intéressé un jour aux fondements des mathématiques, puis une fois que j'ai eu le sentiment que tout était réglé, je me suis mis à travailler au quotidien sans forcément me demander dans quelle axiomatique je me place. Et je ne connais même pas par cœur les axiomes de ZF.
La logique était une passion de jeunesse, au point d'avoir validé le DEA (à l'époque) "Logiques et fondement de l'informatique" de Paris VII, et commencé une thèse de théorie des modèles. Puis je je me suis rendu compte que c'était très technique quand même, et j'ai bifurqué.
Ce fil me fait rajeunir de vingt ans.
Sirgab a écrit:Les paradoxes de Zénon sont liés à la confusion entre l'infini en puissance et l'infini en acte. En suivant Aristote, on peut dire que l'infini n'existe pas en acte, mais seulement en puissance. Le continu est divisible à l'infini, mais pour autant il n'est pas divisé à l'infini. En traçant une ligne, je ne trace pas une infinité de points, mais je fais apparaître une divisibilité infinie dans le continu.
Le vocabulaire n'est plus celui qui nous serait familier aujourd'hui, mais franchement, je suis soufflé par l'intuition d'Aristote, si c'est bien sa présentation.
jaybe a écrit:Un joli paradoxe qui semble difficile à trouver en français, en voici une version probablement un peu différente de celle originelle : paradoxe de Benardete (certains auteurs l'ont qualifié de "new Zeno paradox").
Un homme veut se rendre d'une ville A à une ville B.
Sur sa route, une infinité dénombrable de démons veut l'empêcher d'atteindre la ville B.
Pour tout n entier naturel, le démon n décide que lorsque l'homme aura parcouru 1/2^(n+1) du chemin, il dressera aussitôt devant lui un mur infranchissable (le démon 0 décide que lorsque l'homme aura parcouru la moitié du chemin, il dressera aussitôt devant lui un mur infranchissable ; le démon 1 décide que lorsque l'homme aura parcouru le quart du chemin, il dressera aussitôt devant lui un mur infranchissable, etc.).
Si le démon n fabrique le mur qui bloque l'homme, cela implique que le démon n+1 n'a pas fait son boulot, donc aucun démon ne construit de mur et l'homme atteint la ville B.



 JPhMMDemi-dieu
JPhMMDemi-dieu
Comme quoi, on ne peut pas compter jusqu'à l'infini dans les deux sens.

_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
 User17706Bon génie
User17706Bon génie
C'est une présentation très fidèle à ce que dit Aristote. (On suppose qu'Euclide et lui pourraient avoir profité d'un enseignement semblable, je le rappelle: c'est chez Platon qu'on apprenait les meilleures mathématiques de l'époque  )
)
 AndréCNiveau 9
AndréCNiveau 9
Bijection est un bien grand mot pour dire rapidement ce que tout le monde fait sans le savoir lorsqu'il compte :laMiss a écrit:J'ai cliqué par curiosité sur ce topic, sachant pertinemment que je serai larguée et en effet, je me suis arrêtée à "bijection" p.1 !
Je repasserai peut-être poser des questions quand mes neurones se montreront plus tenaces que ce soir !
Par exemple, lorsque vous comptez le nombre d'allumettes (représentés par la lettre i majuscule ci-dessous : I)
I -> 1
II -> 2
III -> 3
IIII -> 4
IIIII -> 5
etc
A chaque paquet d'allumettes correspond un seul nombre et vice versa, à chaque nombre correspond un seul paquet d'allumette. Il y a une bijection entre les paquets d'allumettes et les nombres entiers.
Cette façon de compter qui est la façon de compter « naturelle » pose problème.
Il existe une histoire d'un dialogue de deux mathématiciens Grecs (j'ai oublié lesquels, si quelqu'un sait ?) dans lequel le premier dit au second :
- dans les vingt premiers nombres entiers (1; 2; 3; ...; 20) [le zéro n'existait pas à l'époque] combien y a t-il de nombres pair ?
- assurément la moitié (soit 10) répond le second : 2; 4; 6; 8;10;12;14;16; 18; 20
- le premier lui dit alors « Considère l'ensemble de tous les nombres entiers, combien y-a t-il de nombres pair ? »
- assurément la moitié lui répond le second.
Et le premier lui montre qu'il se trompe, il y en a autant !
Pour ce faire, il considère l'ensemble des nombres entiers 1; 2; 3; 4; 5; 6; etc
puis il multiple par 2 chacun de ceux-ci.
Il obtient :
1 -> 2
2 -> 4
3 -> 6
4 -> 8
5 ->10
6 -> 12
Etc jusqu'à l'infini.
Il y a autant d'entier que de « flèches », et autant de « flèches » que de pairs, donc il y a autant de nombres entiers que de nombres pairs. On vient de créer une bijection, les bijections permettent de compter, de dénombrer.
 William FosterExpert
William FosterExpert
Je ne suis pas certain que tu l'ais désembrouillée 
Tu aurais dû faire la démonstration qu'un cercle contient un point de plus qu'une droite, c'eut été plus intuitif
Tu aurais dû faire la démonstration qu'un cercle contient un point de plus qu'une droite, c'eut été plus intuitif
_________________
Tout le monde me dit que je ne peux pas faire l'unanimité.
"Opinions are like orgasms : mine matters most and I really don't care if you have one." Sylvia Plath
Vérificateur de miroir est un métier que je me verrais bien faire, un jour.
 User17706Bon génie
User17706Bon génie
C'est probablement une attribution factice. Mais je ne sais pas quand au juste ça a été remarqué.AndréC a écrit: Il existe une histoire d'un dialogue de deux mathématiciens Grecs (j'ai oublié lesquels, si quelqu'un sait ?)
Cela dit, l'infinité des nombres premiers est dans Euclide (IX 20), alors bon. Mais cet argument bijectif-là, je suis aussi curieux d'en savoir l'origine (connue) si quelqu'un l'a.
 LaverdureEmpereur
LaverdureEmpereur
William Foster a écrit:Je ne suis pas certain que tu l'ais désembrouillée
Tu aurais dû faire la démonstration qu'un cercle contient un point de plus qu'une droite, c'eut été plus intuitif
J'ai trouvé cela très clair... Par contre je sèche encore sur le cercle contenant un point de plus qu'une droite
_________________

 AndréCNiveau 9
AndréCNiveau 9
J'aurai essayé !William Foster a écrit:Je ne suis pas certain que tu l'ais désembrouillée
Je ne connais pas cette démonstration.William Foster a écrit:
Tu aurais dû faire la démonstration qu'un cercle contient un point de plus qu'une droite, c'eut été plus intuitif
 William FosterExpert
William FosterExpert
Tu prends un cercle, une droite qui lui est tangente en B, et le point A (en haut sur le dessin) du cercle diamétralement opposé à B.AndréC a écrit:Je ne connais pas cette démonstration.
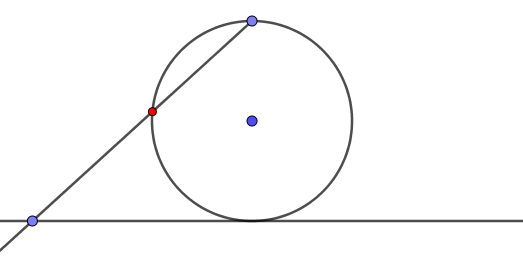
Si maintenant tu prends un point M sur la droite et que tu traces [AM), cette demi-droite coupe le cercle en un seul point N (en rouge sur le dessin). A tout point M correspond un et un seul point N.
Inversement, pour tout point N du cercle, la demi-droite [AN) coupe la droite en un seul point M.
Tout point M est pote avec un seul point N. Tout point N est pote avec un seul point M. Il y a donc autant de points sur la droite que sur le cercle...
...
...
Oui mais non : le point A est le seul à ne pas avoir d'ami sur la droite. Le cercle possède donc un point (le A) de plus que la droite !
Edit : merci de ne pas éreinter la forme de mon explication que j'ai tentée de faire compréhensible aux profanes
_________________
Tout le monde me dit que je ne peux pas faire l'unanimité.
"Opinions are like orgasms : mine matters most and I really don't care if you have one." Sylvia Plath
Vérificateur de miroir est un métier que je me verrais bien faire, un jour.
 LaverdureEmpereur
LaverdureEmpereur
Ah oui, tiens... C'est très clair (ça me laisse rêveur, j'aime bien  ). Du coup, il n'y a pas de bijection entre l'ensemble représenté par le cercle et celui représenté par la droite, c'est ça ?
). Du coup, il n'y a pas de bijection entre l'ensemble représenté par le cercle et celui représenté par la droite, c'est ça ?
_________________

 BrindIfFidèle du forum
BrindIfFidèle du forum
Si tu fais la même chose en partant du centre, tu trouves qu'il a deux points de plus que deux droites 
 JPhMMDemi-dieu
JPhMMDemi-dieu
Tu as oublié le point à l'infini.William Foster a écrit:Tu prends un cercle, une droite qui lui est tangente en B, et le point A (en haut sur le dessin) du cercle diamétralement opposé à B.AndréC a écrit:Je ne connais pas cette démonstration.
Si maintenant tu prends un point M sur la droite et que tu traces [AM), cette demi-droite coupe le cercle en un seul point N (en rouge sur le dessin). A tout point M correspond un et un seul point N.
Inversement, pour tout point N du cercle, la demi-droite [AN) coupe la droite en un seul point M.
Tout point M est pote avec un seul point N. Tout point N est pote avec un seul point M. Il y a donc autant de points sur la droite que sur le cercle...
...
...
Oui mais non : le point A est le seul à ne pas avoir d'ami sur la droite. Le cercle possède donc un point (le A) de plus que la droite !
Edit : merci de ne pas éreinter la forme de mon explication que j'ai tentée de faire compréhensible aux profanes

_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
 William FosterExpert
William FosterExpert
Effectivement.Laverdure a écrit:Ah oui, tiens... C'est très clair. Du coup, il n'y a pas de bijection entre l'ensemble représenté par le cercle et celui représenté par la droite, c'est ça ?
Il y aurait bijection entre la droite et le cercle dans lequel tu aurais enlevé le point A

_________________
Tout le monde me dit que je ne peux pas faire l'unanimité.
"Opinions are like orgasms : mine matters most and I really don't care if you have one." Sylvia Plath
Vérificateur de miroir est un métier que je me verrais bien faire, un jour.
 LaverdureEmpereur
LaverdureEmpereur
BrindIf a écrit:Si tu fais la même chose en partant du centre, tu trouves qu'il a deux points de plus que deux droites
C'est valable aussi si on prend la tangente au point A, non ?
_________________

 William FosterExpert
William FosterExpert
Bouge pas, je vais le chercher...JPhMM a écrit:
Tu as oublié le point à l'infini.

_________________
Tout le monde me dit que je ne peux pas faire l'unanimité.
"Opinions are like orgasms : mine matters most and I really don't care if you have one." Sylvia Plath
Vérificateur de miroir est un métier que je me verrais bien faire, un jour.
 LaverdureEmpereur
LaverdureEmpereur
JPhMM a écrit:Tu as oublié le point à l'infini.William Foster a écrit:Tu prends un cercle, une droite qui lui est tangente en B, et le point A (en haut sur le dessin) du cercle diamétralement opposé à B.AndréC a écrit:Je ne connais pas cette démonstration.
Si maintenant tu prends un point M sur la droite et que tu traces [AM), cette demi-droite coupe le cercle en un seul point N (en rouge sur le dessin). A tout point M correspond un et un seul point N.
Inversement, pour tout point N du cercle, la demi-droite [AN) coupe la droite en un seul point M.
Tout point M est pote avec un seul point N. Tout point N est pote avec un seul point M. Il y a donc autant de points sur la droite que sur le cercle...
...
...
Oui mais non : le point A est le seul à ne pas avoir d'ami sur la droite. Le cercle possède donc un point (le A) de plus que la droite !
Edit : merci de ne pas éreinter la forme de mon explication que j'ai tentée de faire compréhensible aux profanes

Je viens de regarder ça sur internet et justement je me demande, si on considère le point à l'infini (si j'ai bien compris, ça revient à faire bouger le point M vers la gauche donc rendre les droite (AM) et la tangente progressivement "parallèles") est-ce qu'on peut dire que "A sera pote avec M" (
_________________

Page 3 sur 4 •  1, 2, 3, 4
1, 2, 3, 4 
 1, 2, 3, 4
1, 2, 3, 4 
- E. Lévinas, Totalité et Infini (notes de lecture)
- 31.01 / 01.02 2012 : Grand Colloque lettres classiques "Refonder l'enseignement du latin et du grec" (lycée Louis le Grand)
- Agota Kristof, Le Grand Cahier, Grand-Mère
- science étonnante #24 - l'infini
- Désir d'infini : des chiffres, des univers et des hommes
Permission de ce forum:
Vous ne pouvez pas répondre aux sujets dans ce forum


