Page 1 sur 3 • 1, 2, 3 

 cjpNiveau 2
cjpNiveau 2
Salut à tous,
Je m'intéresse au calcul littéral en seconde et je souhaite avoir le point de vue d'autres enseignants, également en sciences physiques ou SI, sur le sujet. Sentez vous libre de répondre à une ou plusieurs ou toutes les questions ! Ou même de converser librement sur le sujet ! Merci beaucoup !
1) difficultés des élèves à l'entrée et en cours de seconde
2) les erreurs types ou réseaux d'erreurs que vous constatez
3) vos outils diagnostiques
4) vos outils de remédiation (efficaces ou inefficaces)
5) la place des TICE dans tout ça
6) en quoi la différenciation vous aide à aider les élèves dans ce cadre ?
A très bientôt
Je m'intéresse au calcul littéral en seconde et je souhaite avoir le point de vue d'autres enseignants, également en sciences physiques ou SI, sur le sujet. Sentez vous libre de répondre à une ou plusieurs ou toutes les questions ! Ou même de converser librement sur le sujet ! Merci beaucoup !
1) difficultés des élèves à l'entrée et en cours de seconde
2) les erreurs types ou réseaux d'erreurs que vous constatez
3) vos outils diagnostiques
4) vos outils de remédiation (efficaces ou inefficaces)
5) la place des TICE dans tout ça
6) en quoi la différenciation vous aide à aider les élèves dans ce cadre ?
A très bientôt
 ycombeMonarque
ycombeMonarque
Bah, c'est facile.
1) ils ne savent rien faire, ne développer ni factoriser, et n'ont rien compris aux fonctions.
2) réseau d'erreur? Les sciences de l'éduc ont encore inventé une nouvelle notion?
3) On fait une interro avec des exos de base. Ils se plantent.
4) Des exos, des exos, des exos. De base. Et des interros. plein.
5) La responsabilité des TICE est énorme. Les élèves confondent allègrement addition et soustraction, tout ça ne sont que touches de la calculatrice.
6) J'attends toujours une différenciation qui permette de réduire l'écart. Pour l'instant, cela ne fonctionne pas.
(Et je n'enseigne pas au lycée).
1) ils ne savent rien faire, ne développer ni factoriser, et n'ont rien compris aux fonctions.
2) réseau d'erreur? Les sciences de l'éduc ont encore inventé une nouvelle notion?
3) On fait une interro avec des exos de base. Ils se plantent.
4) Des exos, des exos, des exos. De base. Et des interros. plein.
5) La responsabilité des TICE est énorme. Les élèves confondent allègrement addition et soustraction, tout ça ne sont que touches de la calculatrice.
6) J'attends toujours une différenciation qui permette de réduire l'écart. Pour l'instant, cela ne fonctionne pas.
(Et je n'enseigne pas au lycée).
_________________
Assurbanipal: "Passant, mange, bois, divertis-toi ; tout le reste n’est rien".
Franck Ramus : "Les sciences de l'éducation à la française se font fort de produire un discours savant sur l'éducation, mais ce serait visiblement trop leur demander que de mettre leur discours à l'épreuve des faits".
 BalthazaardVénérable
BalthazaardVénérable
ycombe a écrit:Bah, c'est facile.
1) ils ne savent rien faire, ne développer ni factoriser, et n'ont rien compris aux fonctions.
2) réseau d'erreur? Les sciences de l'éduc ont encore inventé une nouvelle notion?
3) On fait une interro avec des exos de base. Ils se plantent.
4) Des exos, des exos, des exos. De base. Et des interros. plein.
5) La responsabilité des TICE est énorme. Les élèves confondent allègrement addition et soustraction, tout ça ne sont que touches de la calculatrice.
6) J'attends toujours une différenciation qui permette de réduire l'écart. Pour l'instant, cela ne fonctionne pas.
(Et je n'enseigne pas au lycée).
j'enseigne au lycée et je plussoie ycombe sur tous les points en soulignant le premier qui est une évidence pour n'importe qui à des yeux (mais pas à l'
 cjpNiveau 2
cjpNiveau 2
Merci pour ton retour 
Ah tu enseignes les math ! A quel niveau ?
Pour toi la raison est donc la surutilisation de la calculatrice ?
reseau d erreur : non pas encore du vocabulaire iufm-uesque (ou espeïen), mais lu dans un article sur le sujet. Peut être bientôt, parmi le référentiel bondissant aléatoire, la rupture épistémologique et autres appellations
J'ai mis volontairement 2 sujets pour avoir un retour des profs de SP aussi.
Ah tu enseignes les math ! A quel niveau ?
Pour toi la raison est donc la surutilisation de la calculatrice ?
reseau d erreur : non pas encore du vocabulaire iufm-uesque (ou espeïen), mais lu dans un article sur le sujet. Peut être bientôt, parmi le référentiel bondissant aléatoire, la rupture épistémologique et autres appellations

J'ai mis volontairement 2 sujets pour avoir un retour des profs de SP aussi.
 cjpNiveau 2
cjpNiveau 2
Balthazaard a écrit:ycombe a écrit:Bah, c'est facile.
1) ils ne savent rien faire, ne développer ni factoriser, et n'ont rien compris aux fonctions.
2) réseau d'erreur? Les sciences de l'éduc ont encore inventé une nouvelle notion?
3) On fait une interro avec des exos de base. Ils se plantent.
4) Des exos, des exos, des exos. De base. Et des interros. plein.
5) La responsabilité des TICE est énorme. Les élèves confondent allègrement addition et soustraction, tout ça ne sont que touches de la calculatrice.
6) J'attends toujours une différenciation qui permette de réduire l'écart. Pour l'instant, cela ne fonctionne pas.
(Et je n'enseigne pas au lycée).
j'enseigne au lycée et je plussoie ycombe sur tous les points en soulignant le premier qui est une évidence pour n'importe qui à des yeux (mais pas à l'iuespe semble t-il)
Ah bah si on constate mais on n a pas le droit de le dire ! Disons que j'essaie de récolter les idées ou retours d expérience, à succès de préférence, mais les échecs aussi. A votre avis pourquoi ils ne savent pas factoriser et développer ? Chgt des programmes ? Moins de travail ? Pb de compréhension ? ...
 InvitéInvité
InvitéInvité
1) difficultés des élèves à l'entrée et en cours de seconde
Diviser par 10 sans calculatrice, utiliser et interpréter correctement une puissance de 10 / une écriture scientifique, faire la différence entre une surface et un volume, calculer le perimètre d'un cercle...
2) les erreurs types ou réseaux d'erreurs que vous constatez
Voir supra
3) vos outils diagnostiques
Eval, exercices d'entrainement...
4) vos outils de remédiation (efficaces ou inefficaces)
L'entrainement
5) la place des TICE dans tout ça
Possibilité d'entrainement à la maison, avec suivi de qui fait quoi, et quand.
6) en quoi la différenciation vous aide à aider les élèves dans ce cadre ?
Je ne comprends pas la question
Diviser par 10 sans calculatrice, utiliser et interpréter correctement une puissance de 10 / une écriture scientifique, faire la différence entre une surface et un volume, calculer le perimètre d'un cercle...
2) les erreurs types ou réseaux d'erreurs que vous constatez
Voir supra
3) vos outils diagnostiques
Eval, exercices d'entrainement...
4) vos outils de remédiation (efficaces ou inefficaces)
L'entrainement
5) la place des TICE dans tout ça
Possibilité d'entrainement à la maison, avec suivi de qui fait quoi, et quand.
6) en quoi la différenciation vous aide à aider les élèves dans ce cadre ?
Je ne comprends pas la question
 BalthazaardVénérable
BalthazaardVénérable
la sur-utilisation de la calculatrice a vidé les opérations de leur sens....je ne veux pas discuter du bien fondé ou pas de son usage mais c'est un fait que tu constateras sans doute un jour. pour ma part parler de calcul littéral quand on ne sait pas le sens (en français) des mots somme, produit, quotient, inverse...etc et plus grave quand on est incapable de relier un calcul à ces mots me semble vain..
quelques constatations en vrac 2x+x+2x=4x...difficile 2x+x=3x limite infaisable 2x+0.5x=2.5x impensable (pour la plupart)
2x=0...x=2...x=1/2 x=0 ou 2=0...etc forcément on ne sait pas ce qu'est une multiplication...(par contre on a appris par coeur..un produit est nul...etc)
quelques constatations en vrac 2x+x+2x=4x...difficile 2x+x=3x limite infaisable 2x+0.5x=2.5x impensable (pour la plupart)
2x=0...x=2...x=1/2 x=0 ou 2=0...etc forcément on ne sait pas ce qu'est une multiplication...(par contre on a appris par coeur..un produit est nul...etc)
 TrinityEsprit éclairé
TrinityEsprit éclairé
En physique (je suis en collège) :
- difficulté principale : les maths. Même de base. Pour certains, s'il y a un calcul à faire, c'est le début de la fin.
- erreurs / problèmes : la plupart semble incapable d'utiliser une formule, ils ne font pas le lien entre la grandeur et sa valeur. Beaucoup ne savent pas convertir.
- outil diagnostique : en électricité (lois des intensités et tensions, loi d'ohm, calculs de puissance et énergie et j'en passe), les résultats sont atterrants même quand ce sont des exercices vus et revus.
- remédiation : je n'ai rien trouvé d'efficace, je passe un temps monstre sur les conversions en 5e, 4e et 3e et, visiblement, ça ne sert à rien dans 90% des cas. On fait, corrige, refait, recorrige des exercices d'application directe des formules et le résultat n'est pas meilleur qu'avec les conversions.
- TICE : je ne les utilise pas (je ne compte pas mon vidéoprojecteur).
- différenciation : j'explique autant de fois que possible, de toutes les manières possibles. Certains semblent percuter sur le moment mais n'en retiennent finalement rien.
- difficulté principale : les maths. Même de base. Pour certains, s'il y a un calcul à faire, c'est le début de la fin.
- erreurs / problèmes : la plupart semble incapable d'utiliser une formule, ils ne font pas le lien entre la grandeur et sa valeur. Beaucoup ne savent pas convertir.
- outil diagnostique : en électricité (lois des intensités et tensions, loi d'ohm, calculs de puissance et énergie et j'en passe), les résultats sont atterrants même quand ce sont des exercices vus et revus.
- remédiation : je n'ai rien trouvé d'efficace, je passe un temps monstre sur les conversions en 5e, 4e et 3e et, visiblement, ça ne sert à rien dans 90% des cas. On fait, corrige, refait, recorrige des exercices d'application directe des formules et le résultat n'est pas meilleur qu'avec les conversions.
- TICE : je ne les utilise pas (je ne compte pas mon vidéoprojecteur).
- différenciation : j'explique autant de fois que possible, de toutes les manières possibles. Certains semblent percuter sur le moment mais n'en retiennent finalement rien.
_________________
"Deux choses sont infinies : l'Univers et la bêtise humaine. Mais en ce qui concerne l'Univers, je n'en ai pas encore acquis la certitude absolue." Albert Einstein

 BoubouleDoyen
BoubouleDoyen
Balthazaard a écrit:la sur-utilisation de la calculatrice a vidé les opérations de leur sens....je ne veux pas discuter du bien fondé ou pas de son usage mais c'est un fait que tu constateras sans doute un jour. pour ma part parler de calcul littéral quand on ne sait pas le sens (en français) des mots somme, produit, quotient, inverse...etc et plus grave quand on est incapable de relier un calcul à ces mots me semble vain..
quelques constatations en vrac 2x+x+2x=4x...difficile 2x+x=3x limite infaisable 2x+0.5x=2.5x impensable (pour la plupart)
2x=0...x=2...x=1/2 x=0 ou 2=0...etc forcément on ne sait pas ce qu'est une multiplication...(par contre on a appris par coeur..un produit est nul...etc)
Oui mais il ne s'agirait pas de faire croire qu'ils maîtrisent les calculs à la calculatrice. Cette sur-utilisation n'amène même pas ça.
 BalthazaardVénérable
BalthazaardVénérable
je ne sais pas trop ce que veut dire maitriser un calcul à la calculatrice...le fait est qu'ignorant le sens ce qu'ils tapent si le calcul nécessite un minimum de mise en forme c'est fini
 BoubouleDoyen
BoubouleDoyen
Balthazaard a écrit:je ne sais pas trop ce que veut dire maitriser un calcul à la calculatrice...le fait est qu'ignorant le sens ce qu'ils tapent si le calcul nécessite un minimum de mise en forme c'est fini
Au niveau du secondaire en physique-chimie, c'est simplement taper correctement les chiffres de l'énoncé, les signes des opérations et savoir
 BalthazaardVénérable
BalthazaardVénérable
Sans doute...même ça en effet...et même post bac si tu veux savoir!!
 TrinityEsprit éclairé
TrinityEsprit éclairé
Bouboule a écrit:Balthazaard a écrit:je ne sais pas trop ce que veut dire maitriser un calcul à la calculatrice...le fait est qu'ignorant le sens ce qu'ils tapent si le calcul nécessite un minimum de mise en forme c'est fini
Au niveau du secondaire en physique-chimie, c'est simplement taper correctement les chiffres de l'énoncé, les signes des opérations et savoirlirerecopier le résultat, non ?
Ben même ça...
Comme ils n'ont pas la moindre idée de ce qu'ils font et qu'ils considèrent que la calculatrice est magique, ils ne réfléchissent pas à ce qu'ils font. Ils tapent 2+3 pour calculer 2x3 et t'écrivent donc sans sourciller que 2x3=5. Sans l'unité. Bien entendu.
Et ils ne savent pas utiliser leur machine. Quand elle leur affiche le résultat en écriture scientifique...
_________________
"Deux choses sont infinies : l'Univers et la bêtise humaine. Mais en ce qui concerne l'Univers, je n'en ai pas encore acquis la certitude absolue." Albert Einstein

 ycombeMonarque
ycombeMonarque
collège. 4e/3e cette annéecjp a écrit:Merci pour ton retour
Ah tu enseignes les math ! A quel niveau ?
C'est une des raisons, mais elle vient en bonne place. Les élèves ne réfléchissent plus aux calculs ni aux relations entre nombres. L'addition et la multiplication n'ont comme seul sens que les touches de la calculatrice, comme la racine ou le cos.
Pour toi la raison est donc la surutilisation de la calculatrice ?
Un article écrit par un universitaire en sciences de l'éduc, peut-être?
reseau d erreur : non pas encore du vocabulaire iufm-uesque (ou espeïen), mais lu dans un article sur le sujet. Peut être bientôt, parmi le référentiel bondissant aléatoire, la rupture épistémologique et autres appellations
J'ai mis volontairement 2 sujets pour avoir un retour des profs de SP aussi.
_________________
Assurbanipal: "Passant, mange, bois, divertis-toi ; tout le reste n’est rien".
Franck Ramus : "Les sciences de l'éducation à la française se font fort de produire un discours savant sur l'éducation, mais ce serait visiblement trop leur demander que de mettre leur discours à l'épreuve des faits".
 BoubouleDoyen
BoubouleDoyen
Balthazaard a écrit:Sans doute...même ça en effet...et même post bac si tu veux savoir!!
Je n'ai aucun doute.
Trinity a écrit:Bouboule a écrit:Balthazaard a écrit:je ne sais pas trop ce que veut dire maitriser un calcul à la calculatrice...le fait est qu'ignorant le sens ce qu'ils tapent si le calcul nécessite un minimum de mise en forme c'est fini
Au niveau du secondaire en physique-chimie, c'est simplement taper correctement les chiffres de l'énoncé, les signes des opérations et savoirlirerecopier le résultat, non ?
Ben même ça...
Comme ils n'ont pas la moindre idée de ce qu'ils font et qu'ils considèrent que la calculatrice est magique, ils ne réfléchissent pas à ce qu'ils font. Ils tapent 2+3 pour calculer 2x3 et t'écrivent donc sans sourciller que 2x3=5. Sans l'unité. Bien entendu.
Et ils ne savent pas utiliser leur machine. Quand elle leur affiche le résultat en écriture scientifique...
C'est bien ce que je veux dire.
(Pour moi c'est très proche de leur incapacité à écrire en français correctement ; il doit y avoir une méta-compétence non acquise derrière tout ça...)
 cjpNiveau 2
cjpNiveau 2
Et vous trouvez que c'est de pire en pire ou pareil tous les ans ?
Comment expliqueriez vous le fait que les élèves ne donnent plus de sens aux calculs qu'ils font ? Ou alors ça a toujours été comme cela, c'est très long à construire ?
Comment expliqueriez vous le fait que les élèves ne donnent plus de sens aux calculs qu'ils font ? Ou alors ça a toujours été comme cela, c'est très long à construire ?
 ptitMarcassinNiveau 2
ptitMarcassinNiveau 2
Je ne suis que stagiaire, je ne peux parler de ce que j'ai vu durant ces quelques mois.
Je vous rejoins sur l'utilisation de la calculatrice, ne maîtrisant pas les parenthèses et ne voyant pas leurs utilités, on arrive à des aberrations et en plus ils ne sont pas capables de se remettre en question.
exemple vécu en seconde:
Calcul de longueur avec les coordonnées de deux points.
le calcul racine((3-5)^2+(1-2)^2) devient une fois tapée à la calculatrice racine(3-5^2+1-2^2) et quand la calculatrice renvoie erreur, on accuse la calculatrice de ne pas fonctionner correctement.
l
Je vous rejoins sur l'utilisation de la calculatrice, ne maîtrisant pas les parenthèses et ne voyant pas leurs utilités, on arrive à des aberrations et en plus ils ne sont pas capables de se remettre en question.
exemple vécu en seconde:
Calcul de longueur avec les coordonnées de deux points.
le calcul racine((3-5)^2+(1-2)^2) devient une fois tapée à la calculatrice racine(3-5^2+1-2^2) et quand la calculatrice renvoie erreur, on accuse la calculatrice de ne pas fonctionner correctement.
l
 cjpNiveau 2
cjpNiveau 2
Ps: j'ai moi aussi constaté les confusions entre multiplication et addition, l'inversion des termes dans la soustraction, les difficultés avec les unités dans des calculs de vitesses pour l EPS, le developpement/factorisation autant avec des nombres qu'avec des lettres, les incompréhensions de l'écriture scientifique sur la calculatrice...
 HélipsProphète
HélipsProphète
Des redites, mais c'est le jeu.
Je suis en math en lycée.
1) difficultés des élèves à l'entrée et en cours de seconde
manipulation des identités remarquables, toute forme de factorisation, la plupart des développements ("madame, je ne me souviens plus si le moins devant la parenthèse ça change tous les signes" et "quand le moins est derrière la parenthèse, ça change aussi ?"). Les calculs sur les fractions.
Forcément, les fonctions, ça ne passe pas.
Confondre somme et produit donne des élèves qui sont incapables (mais réellement, ce n'est pas toujours un manque de volonté) d'apprendre les formules. Les coordonnées du milieu d'un segment par exemple donnent au hasard (x-x')/2, x+x'/2 (oui oui, sans les parenthèses), x^2+x'^2 (sur 2 ou pas).
2) les erreurs types ou réseaux d'erreurs que vous constatez
On mélange somme et produit, on joue à pile ou face pour savoir ce que "passer de l'autre côté" va donner. Les parenthèses sont purement décoratives, elles vont, elles viennent. Non respect des notations, ce qui donne un gloubiboulga dans la tête : (AB) , AB ou le vecteur, tout ça c'est pareil, donc, une fois les vecteurs abordés, on me demande "dans quel sens elle va, la droite ?".
3) vos outils diagnostiques
Les questions qu'ils posent, les interros.
4) vos outils de remédiation (efficaces ou inefficaces)
De jolies fiches de calculs niveau 5ème, mais je nierai tout si mon IPR lit ceci.
Un truc qui marchait pas si mal il y a encore 2 ou 3 ans, c'est la correction "technique" du contrôle. Au lieu de leur rédiger un corrigé rédigé, je n'indique que "puisque la question comporte ceci, il est probable qu'il faille tenter une factorisation/un développement" ou "Attention à l'identité remarquable" sans plus de détail. C'est une façon de faire qui marche bien avec des élèves qui reprennent vraiment le devoir.
5) la place des TICE dans tout ça
Ni bien ni mal. Si au moins ils pouvaient arrêter le "madame, j'obtiens pas le même résultat avec la calculatrice" pour passer à "Madame, je me suis trompé sur ma calculatrice, mais je ne sais pas où".
6) en quoi la différenciation vous aide à aider les élèves dans ce cadre ?
à 35 ? Je fais très peu de différenciation. Si ce n'est pour donner une liste d'exercices un peu plus longue aux meilleurs, mais sans correction du coup.
Je suis en math en lycée.
1) difficultés des élèves à l'entrée et en cours de seconde
manipulation des identités remarquables, toute forme de factorisation, la plupart des développements ("madame, je ne me souviens plus si le moins devant la parenthèse ça change tous les signes" et "quand le moins est derrière la parenthèse, ça change aussi ?"). Les calculs sur les fractions.
Forcément, les fonctions, ça ne passe pas.
Confondre somme et produit donne des élèves qui sont incapables (mais réellement, ce n'est pas toujours un manque de volonté) d'apprendre les formules. Les coordonnées du milieu d'un segment par exemple donnent au hasard (x-x')/2, x+x'/2 (oui oui, sans les parenthèses), x^2+x'^2 (sur 2 ou pas).
2) les erreurs types ou réseaux d'erreurs que vous constatez
On mélange somme et produit, on joue à pile ou face pour savoir ce que "passer de l'autre côté" va donner. Les parenthèses sont purement décoratives, elles vont, elles viennent. Non respect des notations, ce qui donne un gloubiboulga dans la tête : (AB) , AB ou le vecteur, tout ça c'est pareil, donc, une fois les vecteurs abordés, on me demande "dans quel sens elle va, la droite ?".
3) vos outils diagnostiques
Les questions qu'ils posent, les interros.
4) vos outils de remédiation (efficaces ou inefficaces)
De jolies fiches de calculs niveau 5ème, mais je nierai tout si mon IPR lit ceci.
Un truc qui marchait pas si mal il y a encore 2 ou 3 ans, c'est la correction "technique" du contrôle. Au lieu de leur rédiger un corrigé rédigé, je n'indique que "puisque la question comporte ceci, il est probable qu'il faille tenter une factorisation/un développement" ou "Attention à l'identité remarquable" sans plus de détail. C'est une façon de faire qui marche bien avec des élèves qui reprennent vraiment le devoir.
5) la place des TICE dans tout ça
Ni bien ni mal. Si au moins ils pouvaient arrêter le "madame, j'obtiens pas le même résultat avec la calculatrice" pour passer à "Madame, je me suis trompé sur ma calculatrice, mais je ne sais pas où".
6) en quoi la différenciation vous aide à aider les élèves dans ce cadre ?
à 35 ? Je fais très peu de différenciation. Si ce n'est pour donner une liste d'exercices un peu plus longue aux meilleurs, mais sans correction du coup.
_________________
Un jour, je serai prof, comme ça je serai toujours en vacances.
 BrindIfFidèle du forum
BrindIfFidèle du forum
Quelques erreurs fréquentes constatées en 2de, mais en 1re et Tle également : confusion entre antécédent et image (par exemple pour résoudre l'équation f(x)=0, ils calculent f(0)), confusion entre carré et double (très très fréquent  ), incompréhension complète de ce qu'est une fraction (je citais sur un autre fil un élève qui s'était exclamé "Ah bon, c'est un nombre ?" au sujet de 1/2).
), incompréhension complète de ce qu'est une fraction (je citais sur un autre fil un élève qui s'était exclamé "Ah bon, c'est un nombre ?" au sujet de 1/2).
Pas tout à fait dans le sujet, mais un peu trop codé pour être posté dans "Perles de nos élèves", j'ai donné aujourd'hui en Tle un exo où il fallait calculer l'image de 1 par la fonction f: x->2lnx -x. Cela fait trois semaines que l'on étudie la fonction logarithme, on l'a tracée, dérivée, utilisée dans des équations, etc. Un élève écrit "f(1)=2ln -1". Ben oui. Parce que "multiplier par 1, ça fait rien, donc on peut retirer le 1." Plusieurs autres ont opiné de la tête, visiblement c'était clair et logique comme raisonnement.

Pas tout à fait dans le sujet, mais un peu trop codé pour être posté dans "Perles de nos élèves", j'ai donné aujourd'hui en Tle un exo où il fallait calculer l'image de 1 par la fonction f: x->2lnx -x. Cela fait trois semaines que l'on étudie la fonction logarithme, on l'a tracée, dérivée, utilisée dans des équations, etc. Un élève écrit "f(1)=2ln -1". Ben oui. Parce que "multiplier par 1, ça fait rien, donc on peut retirer le 1." Plusieurs autres ont opiné de la tête, visiblement c'était clair et logique comme raisonnement.

 cjpNiveau 2
cjpNiveau 2
Merci.
Une précision sur ma question sur les TICE : je ne demandait pas quelle est la responsabilité des TICE dans les difficultés des élèves (quoique votre avis sur la question m'intéresse aussi) mais quelle place elles pourraient avoir pour les aider éventuellement, ce qui fonctionne ou pas, d'après votre expérience.
Personnellement j'ai expérimenté que l'algorithmique peut parfois décoincer un peu la compréhension de ce qu'est une variable ou une inconnue pour quelques élèves par exemple.
Une précision sur ma question sur les TICE : je ne demandait pas quelle est la responsabilité des TICE dans les difficultés des élèves (quoique votre avis sur la question m'intéresse aussi) mais quelle place elles pourraient avoir pour les aider éventuellement, ce qui fonctionne ou pas, d'après votre expérience.
Personnellement j'ai expérimenté que l'algorithmique peut parfois décoincer un peu la compréhension de ce qu'est une variable ou une inconnue pour quelques élèves par exemple.
 neomathÉrudit
neomathÉrudit
cjp a écrit:Comment expliqueriez vous le fait que les élèves ne donnent plus de sens aux calculs qu'ils font ? Ou alors ça a toujours été comme cela, c'est très long à construire ?

Pour un vieux comme moi, qui a fait toute sa scolarité "avant", la réponse est évidente : mettre dans les mains d'un enfant de CE2 une calculatrice est une monstruosité qui l'empêche, dans presque tous les cas, de jamais construire la notion de multiplication et d'addition.
C'est aussi débile que si l'on décidait de leur donner, au nom du progrès, des scooters en EPS (c'est vrai ça, pourquoi courir, il y a des machines qui nous déplacent tellement plus efficacement).
Bien sûr que ce sont des notions difficiles qui ont toujours été très longues à mettre en place. Sauf qu'autrefois, à force d'en faire, d'en refaire et d'en rerefaire jusqu'au lycée, cela finissait par rentrer. Aujourd'hui, comme comme ces notions ne sont plus comprises, tout ce que l'on essaye de construire par dessus ne sont que châteaux de sable.
 BalthazaardVénérable
BalthazaardVénérable
cjp a écrit:Et vous trouvez que c'est de pire en pire ou pareil tous les ans ?
Comment expliqueriez vous le fait que les élèves ne donnent plus de sens aux calculs qu'ils font ? Ou alors ça a toujours été comme cela, c'est très long à construire ?
Cela vient du fait que nos génies-penseurs de l'éducation considèrent que la maitrise technique est sinon superflue, du moins nocive si elle est travaillée pour elle même....donc la prise de conscience de la difficulté du calcul doit être incluse dans celle de la résolution du problème...
Pour être bref, on ne travaille plus la mécanique du calcul, avec les résultats que l'on voit.....
 HélipsProphète
HélipsProphète
Terminale S, pas plus tard que ce matin :
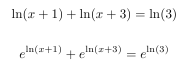
Et il ne comprenait vraiment pas la différence entre sa deuxième ligne et la bonne deuxième ligne.
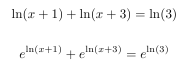
Et il ne comprenait vraiment pas la différence entre sa deuxième ligne et la bonne deuxième ligne.
_________________
Un jour, je serai prof, comme ça je serai toujours en vacances.
 BoubouleDoyen
BoubouleDoyen
BrindIf a écrit:Quelques erreurs fréquentes constatées en 2de, mais en 1re et Tle également : confusion entre antécédent et image (par exemple pour résoudre l'équation f(x)=0, ils calculent f(0)), confusion entre carré et double (très très fréquent), incompréhension complète de ce qu'est une fraction (je citais sur un autre fil un élève qui s'était exclamé "Ah bon, c'est un nombre ?" au sujet de 1/2).
Pas tout à fait dans le sujet, mais un peu trop codé pour être posté dans "Perles de nos élèves", j'ai donné aujourd'hui en Tle un exo où il fallait calculer l'image de 1 par la fonction f: x->2lnx -x. Cela fait trois semaines que l'on étudie la fonction logarithme, on l'a tracée, dérivée, utilisée dans des équations, etc. Un élève écrit "f(1)=2ln -1". Ben oui. Parce que "multiplier par 1, ça fait rien, donc on peut retirer le 1." Plusieurs autres ont opiné de la tête, visiblement c'était clair et logique comme raisonnement.

Des Tles de quelle filière et qui se destinent à quoi ? (C'est juste qu'on remplit APB, là)
Page 1 sur 3 • 1, 2, 3 

Permission de ce forum:
Vous ne pouvez pas répondre aux sujets dans ce forum



