Page 1 sur 2 • 1, 2 

 CeladonDemi-dieu
CeladonDemi-dieu
http://www.agoravox.fr/actualites/societe/article/delires-de-didacticiens-les-127666
 ZorglubHabitué du forum
ZorglubHabitué du forum
cette citation me va très bien ! :
et elle complète agréablement ce que je racontais sur le fil "tâches complexes" :Sous prétexte qu’il existe des aveugles et des borgnes, doit-on crever les yeux à tous les citoyens pour assurer un traitement égal à tous ?
"Je fais remplir un questionnaire par tous les élèves en début d'année scolaire, comme ça je sais repérer très vite ces bâtards de fils de riches blancs hétéros non-divorcés et chrétiens qui risquent de réussir à l'école.
Et je peux prendre toute disposition afin de rétablir plus d'équité en les saquant dès les premiers jours pour les écœurer un peu."
 PatissotDoyen
PatissotDoyen
Celadon a écrit:http://www.agoravox.fr/actualites/societe/article/delires-de-didacticiens-les-127666
 neomathÉrudit
neomathÉrudit
Merci pour le lien. Je vois que je ne suis pas le seul à trouver aberrante la définition officielle du vecteur. Cela me rassure.
 JPhMMDemi-dieu
JPhMMDemi-dieu
La citation la plus marquante est quand même la fameuse définition de la translationZorglub a écrit:cette citation me va très bien ! :
et elle complète agréablement ce que je racontais sur le fil "tâches complexes" :Sous prétexte qu’il existe des aveugles et des borgnes, doit-on crever les yeux à tous les citoyens pour assurer un traitement égal à tous ?
"Je fais remplir un questionnaire par tous les élèves en début d'année scolaire, comme ça je sais repérer très vite ces bâtards de fils de riches blancs hétéros non-divorcés et chrétiens qui risquent de réussir à l'école.
Et je peux prendre toute disposition afin de rétablir plus d'équité en les saquant dès les premiers jours pour les écœurer un peu."
« La translation qui transforme A en B transforme C en D de telle sorte que [AC] et [BD] aient mêmes milieux ».
Au passage, même grammaticalement elle ne veut rien dire, puisque, stricto sensu, ils ont "même milieu" et non "mêmes milieux". :lol:
_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
 PatissotDoyen
PatissotDoyen
Y a t-il seulement des définitions qui ait du sens ? 

_________________
« Déjà, certaines portions de ma vie ressemblent aux salles dégarnies d'un palais trop vaste, qu'un propriétaire appauvri renonce à occuper tout entier. »
 CeladonDemi-dieu
CeladonDemi-dieu
c bo komunkamion.
 ZorglubHabitué du forum
ZorglubHabitué du forum
JPhMM a écrit:La citation la plus marquante est quand même la fameuse définition de la translationZorglub a écrit:cette citation me va très bien ! :
et elle complète agréablement ce que je racontais sur le fil "tâches complexes" :Sous prétexte qu’il existe des aveugles et des borgnes, doit-on crever les yeux à tous les citoyens pour assurer un traitement égal à tous ?
"Je fais remplir un questionnaire par tous les élèves en début d'année scolaire, comme ça je sais repérer très vite ces bâtards de fils de riches blancs hétéros non-divorcés et chrétiens qui risquent de réussir à l'école.
Et je peux prendre toute disposition afin de rétablir plus d'équité en les saquant dès les premiers jours pour les écœurer un peu."
« La translation qui transforme A en B transforme C en D de telle sorte que [AC] et [BD] aient mêmes milieux ».
Au passage, même grammaticalement elle ne veut rien dire, puisque, stricto sensu, ils ont "même milieu" et non "mêmes milieux". :lol:
Me fait souvenir de "un vecteur est la classe d'équivalence des bipoints équipollents à un bipoint donné" (équipollent = même milieu pour les non matheux)
Utilisée en 2nde ou 1ère à l'ancienne (et belle car j'étais jeune) époque !
Le pire c'est que 1/4 des classes comprenait ! Mais 10 % des gosses avaient accès à ces classes donc ...
 JPhMMDemi-dieu
JPhMMDemi-dieu
Oui, enfin celle-là ne veut vraiment rien dire... :lol: :lol: :lol:Patissot a écrit:Y a t-il seulement des définitions qui ait du sens ?
« La translation qui transforme A en B transforme C en D de telle sorte que [AC] et [BD] aient mêmes milieux ».
Si une translation transforme A en B et C en D, alors [AC] et [BD] sont parallèles. Je comprends mal dès lors comment ils pourraient avoir même milieu, sauf à être confondus.
Je dis ça, je dis rien, bien sûr.
PS : mais bon, on dira que la définition veut dire quelque chose aux inversions de lettres près... voilà voilà.
_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
 PatissotDoyen
PatissotDoyen
JPhMM a écrit:Oui, enfin celle-là ne veut vraiment rien dire... :lol: :lol: :lol:Patissot a écrit:Y a t-il seulement des définitions qui ait du sens ?
L'ensemble des nombres réels, une fonction, etc... M'en fout je leur fait quand même recopier, pour faire semblant.
 JPhMMDemi-dieu
JPhMMDemi-dieu
De toute façon, sans théorie des ensembles, peu de définitions subsistent. Reste la cuisine.
_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
 JPhMMDemi-dieu
JPhMMDemi-dieu
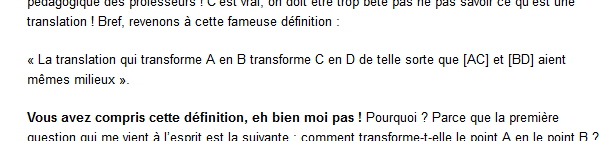
PS pour les non-matheux : en clair, la définition « La translation qui transforme A en B transforme C en D de telle sorte que [AC] et [BD] aient mêmes milieux » de l'article comporte une erreur.
En effet, voyez la figure :
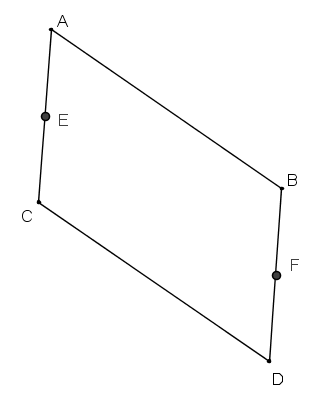
Le translaté de A est B, celui de C est D. Mais E et F, milieux respectifs de [AC] et [BD] ne sont pas confondus.
Vous aurez compris que s'est glissée une inversion de lettres quelque part.
Évidemment, la définition a à voir avec la propriété qui dit que les diagonales d'un parallélogramme se coupent en leur milieu (au singulier, puisqu'il un et un seul milieu commun). Elle est donc : « La translation qui transforme A en B transforme C en D de telle sorte que [AD] et [BC] ont même milieu » (allez savoir pourquoi, je préfère ici l'usage de l'indicatif).
Exemple :
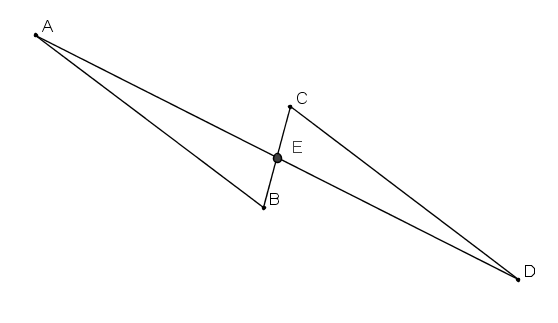
Question subsidiaire : si B et C sont confondus, a-t-on le droit de dire « La translation qui transforme A en B transforme B en D de telle sorte que [AD] et B ont même milieu » ?
_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
 IgniatiusGuide spirituel
IgniatiusGuide spirituel
Cet article est excellent : il confirme ce que je passe mon temps à écrire sur tous les topics de ce forum, à savoir qu'aucun prof de maths de lycée ne peut décemment adhérer à ces nouveaux programmes.
J'ai encore eu une discussion en sdp avec quelques collègues de maths cet après-midi : nous sommes catastrophés par la régression des collégiens qui nous arrivent.
Ils ne savent vraiment plus les choses techniques sur lesquelles nous nous appuyions précédemment, mais le pb, c'est que ce n'est remplacé par rien de nouveau. Il n'y a rien qu'ils sachent mieux faire, c'est dingue d'en arriver à ce constat.
Et l'inspection continue ses délires prétentieux, en annonçant qu'il faut abandonner la technique pour faire "réfléchir les élèves' : mais il est temps de se rendre compte que ce n'est pas possible.
On ne réfléchit pas sur des concepts complexes si l'on n'a pas pratiqué l'aspect technique sérieusement.
Il y a un vrai pb avec les maths : elles ne sont pas une discipline égale aux autres, je suis navré, c'est comme le français.
Il faut rétablir leur prééminence si l'on ne veut pas transformer l'ensemble des autres disciplines en champs de ruines.
PS : concernant les vecteurs, c'est une aberration parmi d'autres. Pour ma part, j'adopte la définition via la construction d'un parallélogramme, mais nous demeurons dans la superficialité, voire la culture générale, car la notion de transformation n'est évidemment pas comprise par nos élèves, et les translations n'ont pas pour but de faire de la géométrie.
Si l'on se conforme scrupuleusement aux programmes, on pourrait se contenter de définir un vecteur comme un couple de coordonnées, quasiment comme un point...
Et dire que certains pensent que ces programmes sont ambitieux...
J'ai encore eu une discussion en sdp avec quelques collègues de maths cet après-midi : nous sommes catastrophés par la régression des collégiens qui nous arrivent.
Ils ne savent vraiment plus les choses techniques sur lesquelles nous nous appuyions précédemment, mais le pb, c'est que ce n'est remplacé par rien de nouveau. Il n'y a rien qu'ils sachent mieux faire, c'est dingue d'en arriver à ce constat.
Et l'inspection continue ses délires prétentieux, en annonçant qu'il faut abandonner la technique pour faire "réfléchir les élèves' : mais il est temps de se rendre compte que ce n'est pas possible.
On ne réfléchit pas sur des concepts complexes si l'on n'a pas pratiqué l'aspect technique sérieusement.
Il y a un vrai pb avec les maths : elles ne sont pas une discipline égale aux autres, je suis navré, c'est comme le français.
Il faut rétablir leur prééminence si l'on ne veut pas transformer l'ensemble des autres disciplines en champs de ruines.
PS : concernant les vecteurs, c'est une aberration parmi d'autres. Pour ma part, j'adopte la définition via la construction d'un parallélogramme, mais nous demeurons dans la superficialité, voire la culture générale, car la notion de transformation n'est évidemment pas comprise par nos élèves, et les translations n'ont pas pour but de faire de la géométrie.
Si l'on se conforme scrupuleusement aux programmes, on pourrait se contenter de définir un vecteur comme un couple de coordonnées, quasiment comme un point...
Et dire que certains pensent que ces programmes sont ambitieux...
_________________
"Celui qui se perd dans sa passion est moins perdu que celui qui perd sa passion."
St Augustin
"God only knows what I'd be without you"
Brian Wilson
 Invité21Fidèle du forum
Invité21Fidèle du forum
Igniatius a écrit:Cet article est excellent : il confirme ce que je passe mon temps à écrire sur tous les topics de ce forum, à savoir qu'aucun prof de maths de lycée ne peut décemment adhérer à ces nouveaux programmes.
J'ai encore eu une discussion en sdp avec quelques collègues de maths cet après-midi : nous sommes catastrophés par la régression des collégiens qui nous arrivent.
Ils ne savent vraiment plus les choses techniques sur lesquelles nous nous appuyions précédemment, mais le pb, c'est que ce n'est remplacé par rien de nouveau. Il n'y a rien qu'ils sachent mieux faire, c'est dingue d'en arriver à ce constat.
Et l'inspection continue ses délires prétentieux, en annonçant qu'il faut abandonner la technique pour faire "réfléchir les élèves' : mais il est temps de se rendre compte que ce n'est pas possible.
On ne réfléchit pas sur des concepts complexes si l'on n'a pas pratiqué l'aspect technique sérieusement.
Il y a un vrai pb avec les maths : elles ne sont pas une discipline égale aux autres, je suis navré, c'est comme le français.
Il faut rétablir leur prééminence si l'on ne veut pas transformer l'ensemble des autres disciplines en champs de ruines.
Voilà, mutatis mutandis, je pourrais écrire la même chose.
 c0c0Niveau 7
c0c0Niveau 7
Effectivement, prof en troisième, j'ai honte des élèves que "je" vais envoyer en seconde !
54 élèves de troisième, un seul qui sait calculer 5x3²-4x3+3 et ils ne comprennent pas pourquoi je crise...
Alors bon courage avec les vecteurs et même les études de fonction (si ça se fait encore!)
54 élèves de troisième, un seul qui sait calculer 5x3²-4x3+3 et ils ne comprennent pas pourquoi je crise...
Alors bon courage avec les vecteurs et même les études de fonction (si ça se fait encore!)
 ZorglubHabitué du forum
ZorglubHabitué du forum
Tout pareil c0c0 ...
Sauf dans une de mes classe : la 4ème CAMIF (machin toutes les options à la con) dans laquelle presque un tiers a un niveau normal !
Sauf dans une de mes classe : la 4ème CAMIF (machin toutes les options à la con) dans laquelle presque un tiers a un niveau normal !
 c0c0Niveau 7
c0c0Niveau 7
Ce qui m'inquiète le plus c'est qu'une de mes deux 3ème est une "3ème camif" avec plus de 20 niveaux A et B+, B, B- sur 29 élèves ! (donc au moins 20 élèves qui vont passer en seconde générale!!)Zorglub a écrit:Tout pareil c0c0 ...
Sauf dans une de mes classe : la 4ème CAMIF (machin toutes les options à la con) dans laquelle presque un tiers a un niveau normal !
 JPhMMDemi-dieu
JPhMMDemi-dieu
Qu'importe, il y a les tâches complexes.c0c0 a écrit:Alors bon courage avec les vecteurs et même les études de fonction (si ça se fait encore!)
_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
 ZorglubHabitué du forum
ZorglubHabitué du forum
Parait même que JeanJau viendra vous seconder.
 c0c0Niveau 7
c0c0Niveau 7
Ah oui mais pour ça c'est moi qui suis nulle 
 IgniatiusGuide spirituel
IgniatiusGuide spirituel
Il y a un commentaire marrant :
"Si t'es un mauvais chercheur, fais de l'enseignement, si t'es un mauvais enseignant, fais de la pédagogie"
La boucle est bouclée aujourd'hui : les "innovateurs" pédagogistes ont la prétention de faire de la recherche...
J'ai autant honte que vous du niveau de mes élèves de TSTI qui vont avoir le bac cette année : j'ai vaguement expérimenté l'an dernier le (non-)esprit des nouveaux programmes avec eux, en tentant de leur faire résoudre des problèmes alors que plus de la moitié s'est arrêtée de progresser en 5è.
Cette année, je reviens aux fondamentaux : activités, cours, méthodes, applications.
C'est dur pour eux, mais ils progressent enfin, à peu près globalement.
Et en sont contents car ils ont enfin le sentiment d'apprendre, pour comprendre après.
"Si t'es un mauvais chercheur, fais de l'enseignement, si t'es un mauvais enseignant, fais de la pédagogie"
La boucle est bouclée aujourd'hui : les "innovateurs" pédagogistes ont la prétention de faire de la recherche...
J'ai autant honte que vous du niveau de mes élèves de TSTI qui vont avoir le bac cette année : j'ai vaguement expérimenté l'an dernier le (non-)esprit des nouveaux programmes avec eux, en tentant de leur faire résoudre des problèmes alors que plus de la moitié s'est arrêtée de progresser en 5è.
Cette année, je reviens aux fondamentaux : activités, cours, méthodes, applications.
C'est dur pour eux, mais ils progressent enfin, à peu près globalement.
Et en sont contents car ils ont enfin le sentiment d'apprendre, pour comprendre après.
_________________
"Celui qui se perd dans sa passion est moins perdu que celui qui perd sa passion."
St Augustin
"God only knows what I'd be without you"
Brian Wilson
 IgniatiusGuide spirituel
IgniatiusGuide spirituel
A lire aussi, sur le même thème à peu près :
http://education.francetv.fr/article/le-role-des-mathematiques-matiere-a-penser-o29222
Une analyse intéressante de l'image des maths, et des pbs qui nous préoccupent aujourd'hui.
http://education.francetv.fr/article/le-role-des-mathematiques-matiere-a-penser-o29222
Une analyse intéressante de l'image des maths, et des pbs qui nous préoccupent aujourd'hui.
_________________
"Celui qui se perd dans sa passion est moins perdu que celui qui perd sa passion."
St Augustin
"God only knows what I'd be without you"
Brian Wilson
 JPhMMDemi-dieu
JPhMMDemi-dieu
Ça donne envie.Zorglub a écrit:Parait même que JeanJau viendra vous seconder.
_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
 User5899Demi-dieu
User5899Demi-dieu
Certes. Mais je ne pige rien, là. [AC] et [BD] sont-ils confondus ? Sinon, ils sont parallèles, non ? Et donc n'ont pas le même milieu... :shock:JPhMM a écrit:La citation la plus marquante est quand même la fameuse définition de la translation
Au passage, même grammaticalement elle ne veut rien dire, puisque, stricto sensu, ils ont "même milieu" et non "mêmes milieux". :lol:« La translation qui transforme A en B transforme C en D de telle sorte que [AC] et [BD] aient mêmes milieux ».
C'est [AD] et [BC] qui vont avoir le même milieu, non ?
 User5899Demi-dieu
User5899Demi-dieu
Bon, je ne sais pas si j'ai tout bien compris dans ce qui précède...Igniatius a écrit:Cet article est excellent : il confirme ce que je passe mon temps à écrire sur tous les topics de ce forum, à savoir qu'aucun prof de maths de lycée ne peut décemment adhérer à ces nouveaux programmes.
J'ai encore eu une discussion en sdp avec quelques collègues de maths cet après-midi : nous sommes catastrophés par la régression des collégiens qui nous arrivent.
Ils ne savent vraiment plus les choses techniques sur lesquelles nous nous appuyions précédemment, mais le pb, c'est que ce n'est remplacé par rien de nouveau. Il n'y a rien qu'ils sachent mieux faire, c'est dingue d'en arriver à ce constat.
Mais Igniatius, c'est exactement ça. Exactement ce qui est en gras.
Page 1 sur 2 • 1, 2 

- [Maths] EDT déséquilibré pour les élèves : comment faire au mieux ?
- [maths] Recruter ou non des professeurs de maths qui n'ont pas un BAC+5 en maths ?
- Anne Coffinier nous salue : l'enseignement privé hors contrat se porte de mieux en mieux.
- Quelles annales de maths (maths expertes en terminale) conseilleriez vous ?
- "Mieux rémunérées, mieux accompagnées, les nouvelles carrières enseignantes"
Permission de ce forum:
Vous ne pouvez pas répondre aux sujets dans ce forum



