Petite question sur la résolution de problèmes additifs

Bonjour

Trouvez-vous plus cohérent de modéliser un problème additif (et donc soustractif) en termes :
- de partie + partie = tout;
- de transformation d'une situation initiale.

Veuillez m'excuser par avance pour la naïveté éventuelle de ma question...

Bonne question !

Faudrait peut-être des exemples : 1) de problèmes 2) de modélisation.

En tout cas, j'en ai de très bonnes sur la multiplication et la division. (affiche extraite de "Le calcul au cours élémentaire" in Chatelet et Bompard dir., L'enseignement de l'arithmétique, 1959.



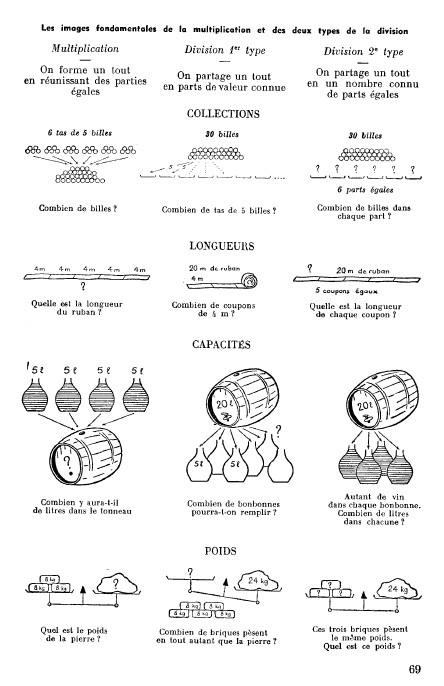
Pour l'addition et la soustraction, cherche dans le même article : "Le calcul au cours élémentaire" qui est magistral. http://michel.delord.free.fr/chatelet/chatelet-arithm.html

Singapour propose des trucs intéressants. Regarde aussi dans les manuels anciens (voir ma signature) ce qu'ils proposent.

Julinette a écrit:Bonjour

Trouvez-vous plus cohérent de modéliser un problème additif (et donc soustractif) en termes :
- de partie + partie = tout;
- de transformation d'une situation initiale.

Veuillez m'excuser par avance pour la naïveté éventuelle de ma question...

Bonjour,
- partie + partie = tout

Non, je ne pense pas que ca puisse modeliser un probleme additif.
Un probleme de division, eventuellement: tout / n = partie. Je dis eventuellement puisqu une partie est elle meme divisible.
Mais partie + partie = tout me semble etre un dogme. Une part de gateau + une part de gateau = 2 parts de gateau, non pas (forcement) un gateau.

Transformation d une situation initiale? je ne comprends pas du tout.

Oui, justement, Singapour modélise par parties et tout.
Et les manuels plus courants préfèrent la transformation.
Voilà pourquoi je m'interrogeais...

Je vais lire l'article de Monsieur Delord.
Merci à vous, Spinoza.

Julinette a écrit:Oui, justement, Singapour modélise par parties et tout.
Et les manuels plus courants préfèrent la transformation.
Voilà pourquoi je m'interrogeais...

Je vais lire l'article de Monsieur Delord.
Merci à vous, Spinoza.

Julinette, qu appelles tu Transformation?

Bonsoir Suecia,

Soit le problème suivant, d'une infinie complexité :
Il n'y a plus dans le plat que 3 parts de pizza Paysanne (lardons, crème fraîche... ma préférée, mais déconseillée dans les régimes hypocaloriques). Maman en donne 2 à mon goinfre de frangin.
Combien m'en reste-t-il ?

- soit je fais partie + partie = tout (soit 2+ ? = 3)
- soit je me fonde sur une sorte de chronologie événementielle :
1) au départ : 3
2) transformation : on enlève 2
3) situation finale : 3 - 2

Il me semble que ces 2 raisonnements n'entraînent pas le même type de modélisation par un schéma, mais peut-être me trompé-je.

Julinette a écrit:Oui, justement, Singapour modélise par parties et tout.
Et les manuels plus courants préfèrent la transformation.
Voilà pourquoi je m'interrogeais...

Je vais lire l'article de Monsieur Delord Bompard.
Merci à vous toi, Spinoza.

Ok, je comprends mieux ta question, mais essaie de mettre si tu peux quelques images des choses proposées par des manuels plus courants et de Singapour. Ca sera plus facile que de parler sans exemples.

Tu peux et tu dois me tutoyer, sans vouloir t'offenser, Julinette.

Je recopie la table des matières que j'avais aussi reproduit sur le fil Re: Remarques pour enseigner la multiplication et la division par Spinoza1670 le Lun 18 Juin 2012, 5:25 pm


Ce texte est un chapitre d'un livre consacré à l'enseignement de l'arithmétique au primaire : ENSEIGNEMENT DE L'ARITHMÉTIQUE,
Cahier
rédigé sous la direction de A. CHATELET, professeur à la Sorbonne, M.
BOMPARD, professeur à l'Ecole Normale d'Instituteurs de la Seine.
Par M. ADAM, G. BEY, M. BOMPARD, R. et S. BRANDICOURT, A. CHATELET, M. FABIANI, A. GODIER, Ch. MAILLARY.
CAHIERS DE PEDAGOGIE MODERNE, EDITIONS BOURRELIER,
1^er trimestre 1959

- AVANT-PROPOS par A. CHATELET, Professeur à la Sorbonne, et M. BOMPARD, Professeur à l'École Normale d'Instituteurs de la Seine : Page 3.
- PROGRAMMES ET INSTRUCTIONS OFFICIELS 1945 : Page 5.
- LE CALCUL AU COURS PRÉPARATOIRE par R. BRANDICOURT, Instituteur d'École d'Application; S. BRANDICOURT, Directrice d'École à Paris, et A. CHATELET : Page 24
- LE CALCUL AU COURS ÉLÉMENTAIRE par M. BOMPARD : Page 42.
- LE CALCUL AU COURS MOYEN, par M. BOMPARD et A. CHATELET : Page 80
- L'ENSEIGNEMENT DU SYSTÈME MÉTRIQUE, par A. GODIER, Inspecteur de l'Enseignement primaire de la Seine : Page 130.
- L'ENSEIGNEMENT DE LA GÉOMÉTRIE A L'ÉCOLE PRIMAIRE, par M. ADAM, Inspecteur de l'Enseignement primaire de la Seine. Note de A. CHATELET : Page 145.
- LE CALCUL MENTAL, par M. FABIANI, Directeur de l'École Annexe de l'École Normale d'Instituteurs de la Seine, et M. BOMPARD : Page 166.
- LE CALCUL EN CLASSE DE FIN D'ÉTUDES (Arithmétique - Système métrique -`Géométrie), par A. GODIER : Page 177.
- REMARQUES SUR L'ENSEIGNEMENT DE LA MULTIPLICATION ET DE LA DIVISION, par G. BEY, Directeur d'École Normale du Jura, et Ch. MAILLARY, Directeur de l'École Annexe : Page 191.
- PROBLÈMES d'après des notes de M. BOMPARD et MM. GRENOUILLET et EVERAERE, Instituteurs à l'Ecole annexe de l'EN : Page 200.
- Table détaillée des articles: Page 205

Julinette a écrit:Bonsoir Suecia,

Soit le problème suivant, d'une infinie complexité :
Il n'y a plus dans le plat que 3 parts de pizza Paysanne (lardons, crème fraîche... ma préférée, mais déconseillée dans les régimes hypocaloriques). Maman en donne 2 à mon goinfre de frangin.
Combien m'en reste-t-il ?

- soit je fais partie + partie = tout (soit 2+ ? = 3)
- soit je me fonde sur une sorte de chronologie événementielle :
1) au départ : 3
2) transformation : on enlève 2
3) situation finale : 3 - 2

Il me semble que ces 2 raisonnements n'entraînent pas le même type de modélisation par un schéma, mais peut-être me trompé-je.

ok, je comprends.
Alors je vais surement dire n importe quoi, mais ce qui me gene dans l histoire de la transformation, c est la temporalite qui me semble exterieure a la modelisation arithmetique, et ce qui me gene dans l histoire de partie+partie est que le resultat n est pas un tout, comme le montre ton exemple.

Le tutoiement va m'être difficile, mais je vais y tâcher.
Tout comme je vais tâcher de lire tout cela.
Mais demain !

Bonne nuit à vous !

Merci ! Alors, à demain !
en attendant, je poste ce petit schéma qui me semble correspondre à ton problème :



Je verrais bien le problème comme ça :

J'ai trois parts de pizza (les trois triangles), on en mange deux (les deux encadrés en rouge), il en reste une.
3 pp - 2 pp = 1 pp.
(pp c'est part de pizza en abrégé, unité de mesure du système gastronomique international)

vérification : 1 part restante plus 2 parts dévorées et on retrouve les 3 parts du départ. 1 pp + 2 pp = 3 pp

Donc pour moi c'est dans un premier temps (calcul) : tout - partie a = partie b

Dans un deuxième temps (vérification) : partie a + partie b = tout.

Ce système de cache transparent (plastique transparent rouge) est pas mal du tout pour les problèmes soustractifs. Je ne l'ai jamais utilisé, mais je suis sûr que ça marcherait bien. L'avantage, c'est que ce qu'on enlève et le tout reste toujours visible.

P.68 de l'ouvrage cité, Spinoza, la multiplication avec 0 intercalaire au multiplicateur est envisagée en 2 lignes. C'est dommage, j'aurais aimé voir comment il la traite : ligne de 0 autorisée ou décalage d'un rang ? Perso, j'interdis la ligne de 0 qui ne prouve pas que l'enfant a compris dans quel ordre il travaille à chaque fois qu'il multiplie 2 chiffres.

suecia a écrit:ce qui me gene dans l histoire de la transformation, c est la temporalite qui me semble exterieure a la modelisation arithmétique

Oui, je n'avais pas bien compris la question mais c'est une histoire de représentation du temps.
On peut :
- représenter les deux situations : situation de départ et situation d'arrivée, et modéliser ainsi ce qui se passe de chaque côté du signe =
- modéliser la situation de départ et la modifier en ajoutant ou retirant des éléments à l'aide de caches ou de cadres transparents pour obtenir la situation d'arrivée.
- représenter uniquement la situation d'arrivée en symbolisant par des flèches, des cadres, des croix ... l'ajout ou le retrait effectués.

C'est variable selon les problèmes mais, de manière générale, je pense qu'il faut passer par les trois stades, au moins au début.