Additions de fractions en 5ème

Bonjour,

Je me prends la tête tous les ans avec l'addition de fractions en 5ème, parce que je trouve que les repères de progression nous obligent à faire quelque chose que je trouve totalement absurde, à savoir traiter le cas particulier où les dénominateurs sont multiples l'un de l'autre avant le cas général. De plus quand je le (re)fais en 4ème, je vois bien que le cas général est beaucoup plus simple à appliquer pour les élèves.
Donc je perds du temps à leur expliquer le cas particulier, que 95% des élèves ont oublié en arrivant en 4ème , pour devoir refaire les deux en 4ème... (du moins dans mon collège honnêtement je ne pense pas avoir vu un seul élève qui s'en souvenait, alors que j'ai passé du temps dessus en 5ème)
Le seul petit avantage que je vois à le faire en 5ème est d'utiliser les égalités de fractions, mais bon... si on fait le cas général on peut travailler les simplifications.

En en parlant dans ma famille, on m'a dit : "mais pourquoi tu ne fais pas comme tu veux ?"
Du coup, je m'interroge : qu'en pensez-vous?
Dites-moi si je risque de faire une grosse bêtise (je vois pas l'inspecteur avant des années normalement, ce n'est pas ça qui m'inquiète mais vraiment le fait que les élèves y arrivent).

Spoiler:

C'est le problème des programmes qui sont conçus pour comprendre avant d'appliquer… tout ça pour que beaucoup d'élèves préfèrent appliquer bêtement la solution générale et sous-optimale comme tu l'évoques; sans doute les mêmes qui quelques années après « feront delta » pour résoudre x²-9=0 ou x²+3x=0.

Même problème au lycée...
Ce que je raconte aux élèves, c'est :
- si les dénominateurs sont premiers entre eux, c'est simple : on calcule (ad+bc)/(bd). C'est visuel, en plus.
- sinon, on cherche le ppcm des dénominateurs.

Je vous rassure, ça ne marche pas...

C'est normal, vu que le PPCM n'est plus enseigné en collège (aucune mention dans les programmes ni les repères de progressivité).

Il me semblait donc plus logique de faire :
1) on apprend à caculer (ad+bc)/(bd) ( à tout le monde )
2) on leur montre que si un dénominateur est multiple de l'autre, il y a une méthode plus simple pour obtenir un résultat simplifié :  u/ka + v/a =(u + kv) / ka . (et là on est content si 1/3 des élèves y arrive, mais au moins les autres savent appliquer une méthode qui fonctionne, même si sous-optimale)

Qu'en pensez-vous?

Flo44 a écrit:C'est normal, vu que le PPCM n'est plus enseigné en collège (aucune mention dans les programmes ni les repères de progressivité).

Il me semblait donc plus logique de faire :
1) on apprend à caculer (ad+bc)/(bd)   ( à tout le monde )
2) on leur montre que si un dénominateur est multiple de l'autre, il y a une méthode plus simple pour obtenir un résultat simplifié :   u/ka + v/a =(u + kv) / ka .  (et là on est content si 1/3 des élèves y arrive, mais au moins les autres savent appliquer une méthode qui fonctionne, même si sous-optimale)

Qu'en pensez-vous?

Cela me paraît le bon sens même. Et c'est valable pour tout. D'abord la méthode bourrin qui a l'avantage de toujours marcher. Ensuite seulement les raffinements.

Je suis d'accord pour enseigner directement la méthode générale. Le cas où il y a un multiple commun... je pense qu'il faut juste les décourager avec des nombres un peu grand au dénominateur (mais numérateur petit). Cela devrait quand même les décourager de multiplier bêtement les dénominateurs. On peut utiliser une dpfp pour trouver le ppcm puis le dénominateur commun par exemple  ...  

Comme pour les produits de fractions, je mettais 5 fractions à multiplier entre elles avec plein de simplifications possibles... pour les obliger à réfléchir un peu.

Bon j'ai toujours vu des gros bourrins.

Idem pour les dpfp souvent je demandais de la faire pour deux nombres simples puis d'en déduire celle du produit, ou du cube du produit des deux nombres ...

Bah il y en avait toujours pour recalculer le produit (voire le cube) puis refaire la dpfp.

C'est quoi "dpfp" ??

J'ai toujours fait les cas simples (3/8 + 1/8, puis 5/12 + 2/3, et 3 + 1/6...) avant le cas général où rien ne s'arrange spécialement (2/7 + 5/4, puis 7/6+ 5/4 : et y en a toujours un pour remarquer qu'on aurait pu mettre sur 12 au lieu de 24, puis 8/15 + 9/40). Et toujours de manière ultra-progressive, avec énormément d'entraînements avec des cas variés... Depuis plus de 20 ans, et je n'ai jamais constaté le problème que tu évoques, bizarre...
Rassurez-moi : vous ne mettez pas les formules avec les lettres [(ad+bc)/(bd)], si ???

Idem pour introduire les divisions de fractions en 4ème : on part de ce qu'on sait et/ou de ce qu'on peut trouver, pour ensuite cogiter à une méthode plus générale (je leur demande de "deviner" le résultat de 15/8 : 3/2, leur intuition est généralement bonne, ils divisent "en haut et en bas", on vérifie en remultipliant puisqu'ils viennent de voir la règle de la multiplication, on constate que ça marche, puis je leur montre que la méthode est vite limitée avec 13/10 : 2/3, et je leur ressors la règle déjà vue sur des décimaux "diviser par un nombre revient à multiplier par son inverse" : on teste sur l'exemple, on vérifie que c'est juste en refaisant la multiplication, on note la règle et on traite les exemples).
Je trouve ça au contraire plus "bourrin" de faire faire une méthode générale sur des cas qui pourraient se traiter plus simplement (quel intérêt de transformer 3/8 + 5/24 pour mettre les fractions sur 192 ?! ) et trouver seulement après qu'en fait non, y en avait pas besoin...
Après, pour répondre à ta question, je pense que oui, on a encore une liberté pédagogique alors il FAUT en user et en abuser ! Si toi ça te convient mieux de traiter dans l'ordre que tu évoques, je pense qu'il vaut mieux faire ainsi... Je trouve qu'il n'y a rien de pire que d'enseigner un truc d'une manière qui ne nous convient pas, qui ne nous "parle" pas.

dpfp : décomposition en produit de facteurs premiers

Moi je donnais une règle en français et une en "langage" mathématique, du style pour tous nombres a, b, a' et b' avec b et b' non nuls a/b + a'/b' = (ab' + a'b) / bb'

Pour division, a/b = (a/b) * 1 = (a/b) * b * (1/b) = a * 1/b ...

"uel intérêt de transformer 3/8 + 5/24 pour mettre les fractions sur 192 " => pour le coup je pense qu'ils mettront sur 24 dans cet exemple. Avec 12 et 16 je pense qu'on a plus de chance de trouver des bourrins.

Je suis tout à fait d'accord avec le point de vue de X.Y.U ci-dessus.

Proton a écrit:Moi je donnais une règle en français et une en "langage" mathématique, du style pour tous nombres a, b, a' et b' avec b et b' non nuls a/b + a'/b' = (ab' + a'b) / bb'

Pour division, a/b = (a/b) * 1 = (a/b) * b * (1/b) = a * 1/b ...

euh oui bien sûr, moi je la comprends totalement, mais quel intérêt de formaliser ça ainsi pour les élèves ? (ou alors juste vite fait pour ceux qui ont une sacrée capacité d'abstraction, ce qui ne court pas les classes... :-/ )

Je n'ai jamais entendu parler de cette méthode générale ??? Elle est vraiment dans les programmes ?

Pour moi, au niveau collège, c'est toujours une seule méthode, il faut réduire au même dénominateur avant d'additionner. Donc je ne comprends pas cette histoire de cas particulier et général, en partant de cette règle, il y a plein de cas différents, il ne faut oublier les cas où on peut simplifier : 1/3 + 8/12 .


Vous apprenez vraiment une formule au collège pour additionner deux fractions, et une autre pour soustraire et une autre pour 3 fractions, et encore une autre pour l'addition d'un eniter et d'une fraction, c'est sans fin...

C'est quoi la méthode bourrin pour 3/2 + 5/6 - 2/3 ?  Ce serait : (3*6*3 + 5*3*2 - 2*2*3)/2*6*3 ?


De mon côté, malheureusement depuis la réforme du collège, j'avais respecté les programmes qui nous imposait de voir l'addition en 4ème, et depuis que c'est revenu en 5ème comme avant avec les dénominateurs multiples et bien nous n'avons pas le temps de le faire en 5ème donc on le fait en 4ème.

Il me semble que l'important c'est surtout de comprendre qu'il faut d'abord réduire au même dénominateur, donc bien maîtriser les fractions égales dans les exercices de simplifications ou de comparaisons.
Je ne me souviens pas avoir vu un jour un manuel de collège aborder cette formule générale ? Qui me semble très limitée pour être nommée générale. Dans les problèmes basique où on additionner deux parts d'un tout pour trouver le reste on termine souvent par 1 - a/b va-t-on donner une formule générale du style 1 - a/b  = (b-a)/b ?
A mon avis aborder cette notion avec des formules générales, n'apporte rien d'intéressant. Le but réel n'est pas d'avoir des techniques de calculs fractionnaires apprises par coeur, mais une maîtrise de la notion de fractions et du sens des quatre opérations sur les fractions.

Une formule générale n'apporte rien pour différencier la somme de deux fractions et le produit de deux fractions. La seule formule qui donne du sens c'est : a/d + b/d = (a+b) / d

Si on pense que c'est utile pour les élèves d'avoir une méthode pour calculer 14/15 + 8/45 en passant par (14*45 + 8*15) / 15*45 alors là j'avoue que sans calculatrice je ne demanderais jamais un calcul aussi pénible à des 5ème pour arriver au résultat simplifié et avec calculatrice et bien elle donne directement le résultat...

Parfois c'est pratique de suivre des formules ou des algorithmes sans bien les comprendre comme pour la multiplication (en calcul posé), mais si au final un élève doit poser 5 * 100 pour trouver le résultat c'est pour moi un échec.

Je pense qu'avant c'était très bien de travailler les additions en 5ème, car cela marchait bien mieux sur deux ans que sur une seule année. Tout comme le cosinus ou Thalès que l'on voyait sur 2 ans.

Pour les formules générales on pourrait très bien aussi apprendre Pythagore généralisé directement au lieu de passer du temps sur le cas particulier.

Sinon, pour les additions de fractions, il y a un truc qui me dérange beaucoup c'est quand on demande à des sixièmes d'écrire 4,27 = 4 + 2/10 + 7/100 ou bien que 2/10 + 7/100 = 27/100 alors qu'on n'a pas encore vu l'addition de fractions ?
Et on voit ce genre d'écriture dès le CM2, et souvent on fait comme si les élèves savaient que 2/10 = 20/100 alors qu'ils ne connaissent pas la règle. Bref, cela apporte beaucoup de confusion dans la tête des élèves, même chose pour 20/100 + 7/100 = 27/100, on considère que c'est une évidence sauf que c'est évident uniquement pour ceux qui connaissent la règle.

De la même manière que les élèves savent que 20 unités et 7 unités font 27 unités, ils conçoivent très bien que 20 centièmes et 7 centièmes font 27 centièmes.
De plus les élèves ont construit l'égalité entre 1 dixième et 10 centièmes notamment en manipulant des outils pédagogiques adaptés. Donc ils savent que 2 dixièmes et 7 centièmes font 27 centièmes.
Tout ça sans connaître la règle d'addition de fractions et ils n'en ont pas besoin à ce moment là de l'apprentissage.

Oui, pour les fractions décimales cela provient de la notion-même de nombre décimal, de ce que représente un dixième, puis un centième (10 fois plus petit qu'un dixième, d'où 10/100 = 1/10), etc, et donc les choses du genre 2/10 + 7/100 = 27/100 ne se conçoivent pas en utilisant une règle d'addition des fractions, mais simplement en se rapportant au sens que représentent les 7 centièmes par exemple...
Pour tout le reste, je suis bien d'accord, ces formules m'ont fait bondir, je pensais à tous mes élèves qui ont très bien géré les additions de fractions cette année et qui auraient été largués avec une formule qui leur fait perdre le sens de tout ça... (bon, malgré tout, j'en ai quand même quelques uns qui n'y arrivaient pas, hein, on ne fait pas de miracles non plus avec certains élèves ayant des lacunes bien ancrées ! )

En tant qu'ancien très très mauvais élève en mathématiques, la mise au même dénominateur est une des choses que j'ai comprise et appliquée sans problème au milieu des années 1980 au collège. C'est l'avis d'un élève devenu professeur. J'avais bien compris qu'il fallait/ qu'on pouvait simplifier si possible. Mais ce n'était pas aussi "simple" dans ma tête. Je n'arrivais pas à apprendre/comprendre les critères de divisibilité et les PPCM/PGCD c'était trop abstrait pour ma petite tête de 6ème ou 5ème.

Manu7 a écrit:Je n'ai jamais entendu parler de cette méthode générale ??? Elle est vraiment dans les programmes ?

Pour moi, au niveau collège, c'est toujours une seule méthode, il faut réduire au même dénominateur avant d'additionner. Donc je ne comprends pas cette histoire de cas particulier et général, en partant de cette règle, il y a plein de cas différents, il ne faut oublier les cas où on peut simplifier : 1/3 + 8/12 .


Vous apprenez vraiment une formule au collège pour additionner deux fractions, et une autre pour soustraire et une autre pour 3 fractions, et encore une autre pour l'addition d'un eniter et d'une fraction, c'est sans fin...

C'est quoi la méthode bourrin pour 3/2 + 5/6 - 2/3 ?  Ce serait : (3*6*3 + 5*3*2 - 2*2*3)/2*6*3 ?


De mon côté, malheureusement depuis la réforme du collège, j'avais respecté les programmes qui nous imposait de voir l'addition en 4ème, et depuis que c'est revenu en 5ème comme avant avec les dénominateurs multiples et bien nous n'avons pas le temps de le faire en 5ème donc on le fait en 4ème.

Il me semble que l'important c'est surtout de comprendre qu'il faut d'abord réduire au même dénominateur, donc bien maîtriser les fractions égales dans les exercices de simplifications ou de comparaisons.
Je ne me souviens pas avoir vu un jour un manuel de collège aborder cette formule générale ? Qui me semble très limitée pour être nommée générale. Dans les problèmes basique où on additionner deux parts d'un tout pour trouver le reste on termine souvent par 1 - a/b va-t-on donner une formule générale du style 1 - a/b  = (b-a)/b ?
A mon avis aborder cette notion avec des formules générales, n'apporte rien d'intéressant. Le but réel n'est pas d'avoir des techniques de calculs fractionnaires apprises par coeur, mais une maîtrise de la notion de fractions et du sens des quatre opérations sur les fractions.

Une formule générale n'apporte rien pour différencier la somme de deux fractions et le produit de deux fractions. La seule formule qui donne du sens c'est : a/d + b/d = (a+b) / d

Si on pense que c'est utile pour les élèves d'avoir une méthode pour calculer 14/15 + 8/45 en passant par (14*45 + 8*15) / 15*45 alors là j'avoue que sans calculatrice je ne demanderais jamais un calcul aussi pénible à des 5ème pour arriver au résultat simplifié et avec calculatrice et bien elle donne directement le résultat...

Parfois c'est pratique de suivre des formules ou des algorithmes sans bien les comprendre comme pour la multiplication (en calcul posé), mais si au final un élève doit poser 5 * 100 pour trouver le résultat c'est pour moi un échec.

Je pense qu'avant c'était très bien de travailler les additions en 5ème, car cela marchait bien mieux sur deux ans que sur une seule année. Tout comme le cosinus ou Thalès que l'on voyait sur 2 ans.

Pour les formules générales on pourrait très bien aussi apprendre Pythagore généralisé directement au lieu de passer du temps sur le cas particulier.

Sinon, pour les additions de fractions, il y a un truc qui me dérange beaucoup c'est quand on demande à des sixièmes d'écrire 4,27 = 4 + 2/10 + 7/100 ou bien que 2/10 + 7/100 = 27/100 alors qu'on n'a pas encore vu l'addition de fractions ?
Et on voit ce genre d'écriture dès le CM2, et souvent on fait comme si les élèves savaient que 2/10 = 20/100 alors qu'ils ne connaissent pas la règle. Bref, cela apporte beaucoup de confusion dans la tête des élèves, même chose pour 20/100 + 7/100 = 27/100, on considère que c'est une évidence sauf que c'est évident uniquement pour ceux qui connaissent la règle.

Dans cette histoire de fractions décimales, ce n'est pas ce qui me dérange.
Dès le CM, ils sont censés travailler sur les équivalences entre unité, dixièmes, centièmes et je dirais que jusqu'en 6e, il est finalement assez naturel pour eux que 2/10=20/100 et que les égalités du type 2+1/10+3/100 = 2+13/100 sont généralement maîtrisées et relèvent de la définition des nombres décimaux.

Par contre, ce qui me dérange est que, dès qu'on a travaillé l'addition de fractions en 5e, ils ne savent plus faire 2/10+5/100 ....
Certainement parce qu'ils n'y voient plus des dixièmes et des centièmes qu'ils connaissent bien ....
Et personnellement, je n'ai pas le temps de m'attarder sur ça pour leur faire remarquer qu'ils savent déjà puis faire le lien avec la règle d'addition des fractions

Il y a plusieurs façons d'énoncer les règles. Bien sûr que l'on peut se limiter à pour tous entiers relatifs a, b et c avec c non nul, a/c + b/c = (a+b) / c et faire une phrase pour le cas où elles ne sont pas au même dénominateur ...

Je trouve néanmoins utile de donner des règles avec des lettres pour illustrer la phrase en français. Notamment la règle pour multiplier une fraction, pour tous entiers relatifs a, b et c avec c non nul, a * b/c = a/c * b = (a*b) / c.

Je trouve que la question initiale n’était pas très explicite. Je pense qu'elle était en rapport avec les exercices et les types de calcul que l'on donne, pas sur le cours.

C'est quoi la méthode bourrin pour 3/2 + 5/6 - 2/3 ?  Ce serait : (3*6*3 + 5*3*2 - 2*2*3)/2*6*3 ?

Oui, mais là encore, sur ces petits nombres, rares sont les élèves qui ne vont pas mettre sur 6 toutes les  fractions. Avec 12 et 18, ils sont déjà plus nombreux à calculer 12*18.

edit: peut etre plus simple pour la division pour "justifier" la règle de la division : a/b = [ a*(1/b) ] / [b*(1/b) ]= a*(1/b) ... ?

En CPGE maths (donc au tableau sans calculatrice) demander à un élève de calculer 1/256 + 1/512 est un moyen sûr de le mettre en échec.

Pas dans celles que j'ai fréquentées...

Voltaire a écrit:En CPGE maths (donc au tableau sans calculatrice) demander à un élève de calculer 1/256 + 1/512 est un moyen sûr de le mettre en échec.

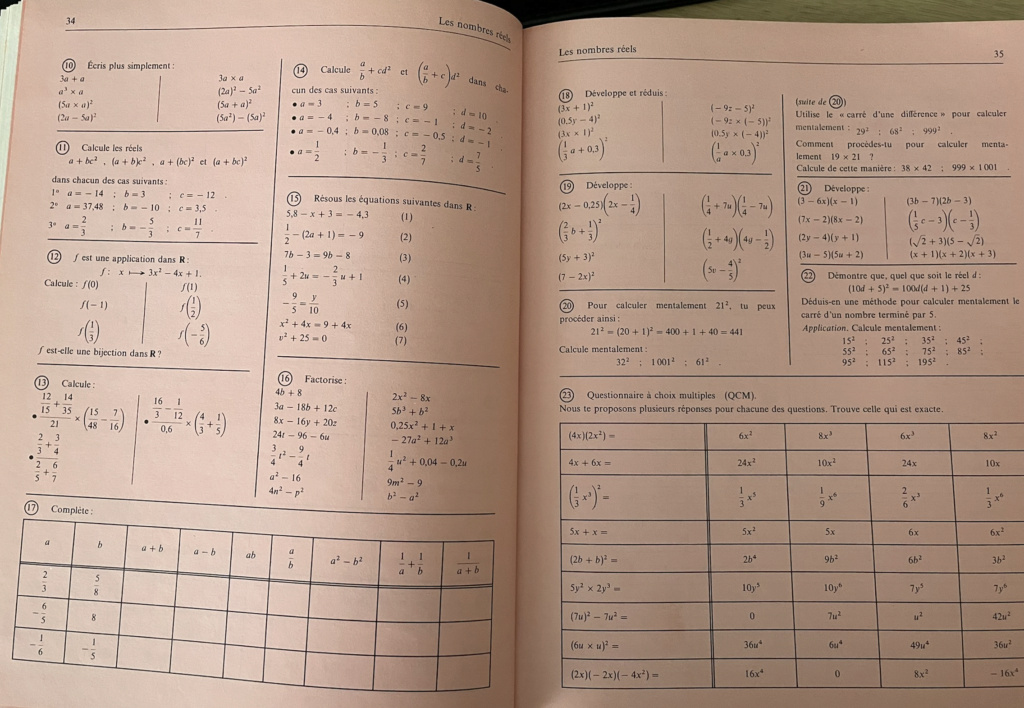
Je viens de retrouver par hasard un livre de 3eme plus âgé que moi ... programme de 1980.

Livre sans fioriture, très clair, bien présenté, sans dessin ridicule, couverture sobre, ... tout le contraire des bouquins d'aujourd'hui.

Quelques extraits ...

Oula c'est vieux oui. Mais je suis surprise de la formule générale pour la somme de fractions. A mon époque (85-89) on nous donnait la formule pour a/d+b/d et on nous disait que pour tous les autres cas on réduit au même dénominateur en cherchant un multiple commun (ppcm recommandé)

Pour illustrer ton propos, PatB, voici cette fois un livre de 4e de 1988 (autre programme ?)

On y traite des additions de fractions comme tu l'évoques

C'est tout à fait comme ça que j'ai appris, puis enseigné.
Je ne crois pas avoir, comme élève, distingué le cas où un dénominateur est multiple de l'autre.
Il faut dire qu'on savait chercher un ppcm (avec la décomposition en produit de facteurs premiers si besoin).

Comme enseignante, j'ai toujours fait chercher un multiple commun (en leur faisant remarquer que le produit des deux n'est pas toujours optimal, notamment quand ils "sont dans la même table " : je leur faisais lister les multiples quand la décomposition en facteurs premiers n'était pas au programme)

chmarmottine a écrit:Dans cette histoire de fractions décimales, ce n'est pas ce qui me dérange.
Dès le CM, ils sont censés travailler sur les équivalences entre unité, dixièmes, centièmes et je dirais que jusqu'en 6e, il est finalement assez naturel pour eux que 2/10=20/100 et que les égalités du type 2+1/10+3/100 = 2+13/100 sont généralement maîtrisées et relèvent de la définition des nombres décimaux.

Par contre, ce qui me dérange est que, dès qu'on a travaillé l'addition de fractions en 5e, ils ne savent plus faire 2/10+5/100 ....
Certainement parce qu'ils n'y voient plus des dixièmes et des centièmes qu'ils connaissent bien ....
Et personnellement, je n'ai pas le temps de m'attarder sur ça pour leur faire remarquer qu'ils savent déjà puis faire le lien avec la règle d'addition des fractions

Oui les élèves savent écrire des décompositions dans le style : 2,13 = 2 + 1/10 + 3/100 = 2 + 13/100 = 213/100

Mais en réalité, je pense sincèrement qu'ils ne maîtrisent pas du tout ce qu'ils écrivent. Il ne faut pas oublier que les programmes passent par ce genre d'écriture pour découvrir l'écriture décimale comme si les élèves devaient maîtriser l'écriture fractionnaire avant de passer à l'écriture décimale, si bien que c'est pour moi totalement abusrde. On a inventé assez tardivement dans l'histoire des maths, l'écriture décimale pour remplacée l'écriture fractionnaire, mais on voudrait que des élèves de CM1 ou CM2 suivent le même chemin. Et on en arrive à des absurdités où on utilise l'écriture décimale pour expliquer 1/10 + 3/100 = 13/100 alors qu'on veut que les élèves maîtrise cette notion pour comprendre que 0,13 est une notation nouvelle pour remplacer 13/100 ou 1/10 + 13/100.

Et au final, je suis totalement d'accord avec toi chmarmottine, les élèves n'ont jamais compris réellement pourquoi 1/10 + 3/100 = 13/100, il faisaient ce genre d'exercice par analogie. Sans rien comprendre aux additions de fractions décimales car les règles des fractions décimales égales ou d'additions de fractions égales ne sont pas vues.
En clair on utilise le + comme un symbole de séparation plutôt d'un symbole de calcul... Et si jamais on veut leur dire qu'ils savent déjà additionner des fractions, je pense qu'on est plutôt dans le domaine de l'illusion.

Et le pire dans cette histoire c'est qu'on trouve normal d'additionner des dixièmes et des centièmes sans jamais parler de dénominateurs égaux. Cela revient quelque part à parler de 0,1 + 0,03 sans jamais avoir expliqué comment on posait correctement de ce genre de calcul.

En sixième on écrit 3/10 = 30/100 = 300/1000 mais finalement ces élèves ne connaissent pas encore la règles des fractions égales et pire ne maîtrisent pas vraiment les multiplications par 10, 100 et 1000 !!! On le voit très vite si on demande 3,7/10 = 37/100.

Et quand on commence à expliquer que 3/10 + 9/100 = 30/100 + 9/100 = 39/100 alors que l'élève ne sait pas qu'il faut le même dénominateur pour additionner les numérateurs, je voudrais bien savoir ce qu'il comprend vraiment dans sa tête ?

Et en 5ème, on risque de reprendre ce genre d'exemple pour justement expliquer qu'il faut le même dénominateur pour additionner. Pour moi c'est le serpent qui se mord la queue. Et pire on pourra même partir de 0,3 + 0,09 = 0,39. Ce qui prouve bien au passage que cela ne pas de sens d'expliquer l'écriture décimale en passant par les fractions décimales alors qu'on ne maîtrise pas du tout la notion de fractions.

Pour moi c'est comme demander à apprendre à labourrer avec des boeufs avant de labourrer avec un tracteur.

Tu ne travailles pas cette notion avec la division en 6e ?

Par exemple, pour partager 26 unités en 8 parts égales, on pose la division de 26 par 8.
Chaque part est de 3 unités et il reste 2 unités. On a 26 = 8*3 + 2.

Ensuite, on pousse la division, les 2 unités restantes sont transformées en 20 dixièmes pour être partagées en 8. Comme ce partage est en dixièmes, on ajoute une virgule.
Comment partager 20 dixième en 8 parts égales ?
Chaque part est de 2 dixièmes et il reste 4 dixièmes. On a 20/10 = 8*2/10 + 4/10. Le dernier reste est 4 dixièmes, on a 26 = 8*3,2 + 0,4.

On continue, et on pousse encore plus loin. 4 dixièmes sont transformés en 40 centièmes pour les partager en 8 ... etc.

Oui mais on tourne en rond, tu peux toujours écrire que 20/10 = 16/10 + 4/10 sauf que les élèves ne connaissent pas la règle d'addition des fractions. Donc ils comprennent quoi ?

Tu dis toi-même qu'on ajoute une virgule donc tu parles de division décimale et d'écriture décimale, je ne vois pas bien l'utilité de parler de fractions pour expliquer la division décimale.  
Pour moi nous sommes plutôt dans 20 dixièmes = 8 * 2 dixièmes + 4 dixièmes 
mais en vrai on dira que 20 = 8*2 + 4 tout cela en dixièmes, 
tout comme dans la division 204 / 8, on prendra d'abord 20 dizaines  et 20 = 8*2 + 4 en dizaines,  
on peut aussi écrire : 2,0 = 8 * 0,2 + 0,4 = 1,6 + 0,4 et si on veut on peut aussi écrire 16/10 + 4/10 
mais pour moi ce n'est pas correct d'utiliser pendant 2 ou 3 ans des additions de fractions à des élèves qui ne savent pas additionner des fractions. 

Et le pire c'est qu'on va leur apprendre 1,6 + 0,4 = 2,0 = 2 bien avant l'addition de fractions et pour justifier cela on va passer par 16/10 + 4/10 = 20/10 et bien plus tard on leur expliquera que l'on additionne les numérateurs quand on a le même dénominateur. 

Alors certains diront que 20/10 = 16/10 + 4/10 c'est exactement pareil que 20 dixièmes = 16 dixièmes + 4 dixièmes sauf que pour moi ce n'est pas du tout la même chose. Dans le premier cas on additionne des fractions et dans le second on additionne des quantités entieres de dixièmes. Et pour dire que c'est équivalent, il faut justement maîtriser l'addition des fractions. Et en sixième justement si on représente cette addition sur une droite graduée, comme on dépasse l'unité, il y a un obstacle à franchir puisque le résultat dépasse 1 c'est à dire 10/10 et de nombreux élèves vont dire que 16/10 + 4/10 = 20/20 uniquement en lisant leur résultat sur la droite graduée car pour eux de 0 à 2 on a partagé en 20 parts donc ce sont des vingtièmes et ils n'ont même pas additionné les deux dénominateurs...

Bref ils ne savent toujours pas additionner des fractions. Et pour eux 16/10 + 4/10 n'a pas du tout le même sens que pour nous.

Et c'est très intéressant car on retrouve finalement le même problème quand les élèves écrivent : 3,8 + 2,7 = 5,15