Calculs d'angles en Spécialité Mathématiques?

Bonjour,

A ceux qui ont des classes de spécialité mathématiques en Terminale: est-ce que vous voyez avec vos élèves la formule pour le calcul d'angles à partir du produit scalaire? En jetant un coup d'œil aux sujets de Bac cette notion ne tombe littéralement jamais, et on utilise l'orthogonalité uniquement pour montrer qu'un vecteur est normal à un plan, ou que deux droites ou qu'une droite et un plan sont orthogonaux.

Je sais que l'examen n'est pas le seul paramètre à prendre en compte, mais le programme en mathématiques est très chargé, et avec l'épreuve qui approche en mars j'avoue qu'avec eux je suis à fond dans l'optique "préparation examen". Je ne veux surtout m'attarder à notions "inutiles" et qui risquent de les perturber (ils risquent de passer du temps à travailler cette notion au détriment d'autres plus importantes).

Bref je suis tenté de passer mon chemin même si officiellement elle est au programme, et j'aimerais connaître votre avis. Cela vous arrive-t-il, faute de temps, et surtout dans des classes à examen, de ne pas aborder certaines notions du programme si vous êtes sur qu'il n'y tomberont pas dessus à l'examen?

xsargou a écrit:Bonjour,

A ceux qui ont des classes de spécialité mathématiques en Terminale: est-ce que vous voyez avec vos élèves la formule pour le calcul d'angles à partir du produit scalaire? En jetant un coup d'œil aux sujets de Bac cette notion ne tombe littéralement jamais, et on utilise l'orthogonalité uniquement pour montrer qu'un vecteur est normal à un plan, ou que deux droites ou qu'une droite et un plan sont orthogonaux.

Je sais que l'examen n'est pas le seul paramètre à prendre en compte, mais le programme en mathématiques est très chargé, et avec l'épreuve qui approche en mars j'avoue qu'avec eux je suis à fond dans l'optique "préparation examen". Je ne veux surtout m'attarder à notions "inutiles" et qui risquent de les perturber (ils risquent de passer du temps à travailler cette notion au détriment d'autres plus importantes).

Bref je suis tenté de passer mon chemin même si officiellement elle est au programme, et j'aimerais connaître votre avis. Cela vous arrive-t-il, faute de temps, et surtout dans des classes à examen, de ne pas aborder certaines notions du programme si vous êtes sur qu'il n'y tomberont pas dessus à l'examen?

Cela arrive forcément de ne pas aborder certaines notions ou certaines applications du programme par manque de temps ou par choix de son approche. L'encyclopédisme n'est pas forcément pertinent en enseignement, du moins à ce niveau.

Les années d'épreuve, c'est encore plus le cas, et avec cette folie d'épreuve en mars, ça sera encore plus le cas qu'avec une épreuve en juin. Le problème étant qu'on favorise alors ce qui va probablement tomber à l'épreuve que ce qui serait plus primordial et élémentaire, au risque de tomber sur l'année où une question va porter sur le point qui est au programme et qui n'était pas tombé depuis quinze ans.

Je n'ai pas encore abordé le produit scalaire dans l'espace, mais vu comme je vais être court (et j'ai eu une absence qui ne va pas améliorer les choses) il est fort possible que je passe sur les calculs d'angles.

Il me semble que le calcul d'angle est une application archi-classique du PS. Si vous ne faites pas ça, vous ne faites que des exos d'application directe de la formule du cours ?

Carrie7 a écrit:Il me semble que le calcul d'angle est une application archi-classique du PS. Si vous ne faites pas ça, vous ne faites que des exos d'application directe de la formule du cours ?

Ce qui tombe surtout à plus de 90%, à l'épreuve du bac, c'est utiliser un vecteur normal pour déterminer une équation de plan, puis éventuellement l'intersection de ce plan avec une droite. Personnellement ça ne réjouit pas de préférer le bachotage de l'épreuve à un travail de fond, mais je ne sais pas si je suis prêt à sacrifier mes élèves à mes convictions.

xsargou a écrit:A ceux qui ont des classes de spécialité mathématiques en Terminale: est-ce que vous voyez avec vos élèves la formule pour le calcul d'angles à partir du produit scalaire? En jetant un coup d'œil aux sujets de Bac cette notion ne tombe littéralement jamais, et on utilise l'orthogonalité uniquement pour montrer qu'un vecteur est normal à un plan, ou que deux droites ou qu'une droite et un plan sont orthogonaux.

Je sais que le programme est dense mais ça peut tomber au bac.

Exemple, sujet de 2019 : https://www.apmep.fr/IMG/pdf/S_N-Caledonie_26_11_2019_DV.pdf

Je ne fais pas l'impasse de mon côté. J'ai retravaillé d'ailleurs toutes les expressions du produit scalaire : cos, projeté, normes, coordoonées, ...

Proton a écrit:

xsargou a écrit:A ceux qui ont des classes de spécialité mathématiques en Terminale: est-ce que vous voyez avec vos élèves la formule pour le calcul d'angles à partir du produit scalaire? En jetant un coup d'œil aux sujets de Bac cette notion ne tombe littéralement jamais, et on utilise l'orthogonalité uniquement pour montrer qu'un vecteur est normal à un plan, ou que deux droites ou qu'une droite et un plan sont orthogonaux.

Je sais que le programme est dense mais ça peut tomber au bac.

Exemple, sujet de 2019 : https://www.apmep.fr/IMG/pdf/S_N-Caledonie_26_11_2019_DV.pdf

Je ne fais pas l'impasse de mon côté. J'ai retravaillé d'ailleurs toutes les expressions du produit scalaire : cos, projeté, normes, coordoonées, ...

Ah oui, c'était donc l'année où ça tombe.

Mine de rien, c'est typique : le sujet n'est pas trop inintéressant et artificiel par rapport à d'autres, mais la question A)4) est déconnectée du reste et ne semble être là que pour vérifier que l'élève connaît l'application du produit scalaire au calcul d'angles.

La partie B est pas exemple plus difficile, mais plus intéressante.

Il y a aussi un sujet de 2021 des candidats libres avec une telle question : https://www.apmep.fr/IMG/pdf/Centres_etrangers_1_spe_11_06_2021_DV_FH.pdf

Donc je conseille vraiment de ne pas faire l'impasse.

Merci à tous pour vos réponses, tout particulièrement à toi Proton pour les sujets, j'en avais regardé pas mal mais apparemment pas ceux-là. Je pense finalement que le risque est trop grand et qu'il vaut mieux aborder cette notion, même s'il y a peu de chances qu'elle tombe et même si c'est le cas, 95% de mes élèves l'auront oubliée... Bref on fera un deux ou trois exercices dessus.

Question supplémentaire pour Proton qui a l'air d'être plus familiarisé que moi sur ce point du programme (c'est la première fois que je fais ce chapitre avec mes Term, l'année dernière on avait pas eu le temps de boucler le programme): tu utilises la formule passant par le arccos? Du coup tu définis rigoureusement la fonction arccos où tu la présentes de manière "ésotérique" comme étant le "contraire" du cosinus?

J'ai sans doute un petit déformement de pensée, travaillant dans un établissement de très bon niveau, mais je ne vois pas pourquoi vous parlez de "notion" pour ce calcul d'angle. Je répète, c'est juste un calcul d'application classique de ce chapitre, sans aucun piège. C'est certain que la proposition de Prezbo tombe quasiment tout le temps, mais on ne va pas faire que ça...

Normalement ils ont déjà vu la formule avec le cosinus (souvent prise comme définition). Donc ce n'est plus qu'à réactiver.

Je ne définis pas arccos, normalement ils ont appris à trouver l'angle connaissant le cosinus en 4e ou 3e, il s'agit donc seulement de pianoter sur la calculatrice ... par contre je rappelle de la mettre en degré.

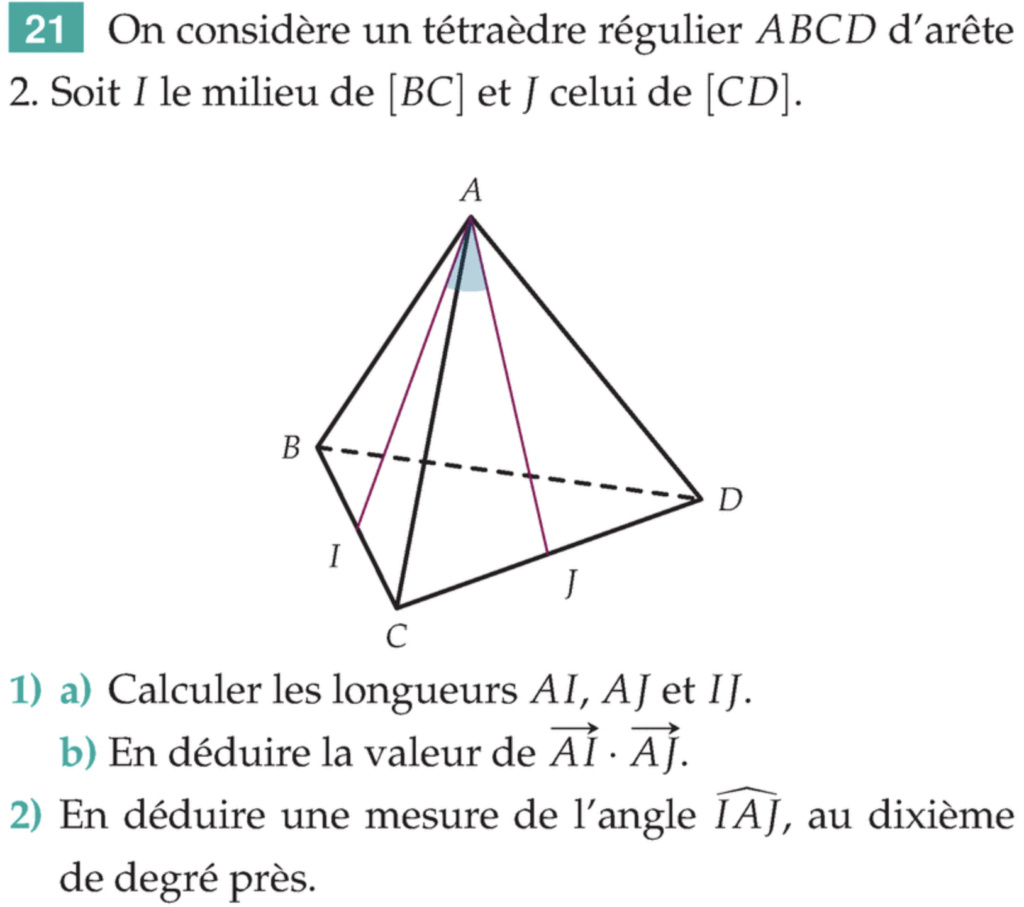
Voilà deux exos de sesamath (l'ancien manuel de TS) que j'ai fait en classe. Il faut calculer une première fois le produit scalaire soit avec les coordonnées (on doit introduire un r.o.n), soit avec la formule des normes.