 thalinaNiveau 3
thalinaNiveau 3
Bonjour,
J'ai un souci avec une de mes classes de sixième.
C'est une classe très hétérogène, avec des élèves qui encore du mal à tracer des angles, simplifier des fractions, etc.
D'autres élèves ont déjà compris dès le premier quart d'heure de la séance et me disent qu'ils s'ennuient.
Parfois, j'envoie ces élèves expliquer aux autres, mais je ne suis pas sûre que leurs explications soient bonnes, puisque la séance suivante, ils ont toujours des difficultés. De plus, leurs "promenades" dans les rangs ne facilitent pas la concentration, d'autant plus que je les ai souvent en dernière heure de l'après midi.
Leur livre comporte de nombreuses méthodes et les exercices restent assez simples, mais pas pour ces élèves en difficulté, et trop faciles pour d'autre élèves qui les font en deux minutes.
Bien sûr, je rajoute des exercices de sésamath ou autres (coloriage magique par exemple) et je les mets une fois par mois en salle info.
Mais certains restent frustrés: l'un d'eux voudrait que je lui apprenne les carrés, racines carrées, ... .
Comment faites-vous face à l'hétérogénéité ?
Quelles ressources pourrais-je utiliser pour ces élèves qui s'ennuient avec ce programme qu'ils ont déjà fait en grande partie au primaire, et prennent plaisir à faire des maths ? Quelle organisation pourrais-je mettre en place ?
Merci pour vos réponses.
J'ai un souci avec une de mes classes de sixième.
C'est une classe très hétérogène, avec des élèves qui encore du mal à tracer des angles, simplifier des fractions, etc.
D'autres élèves ont déjà compris dès le premier quart d'heure de la séance et me disent qu'ils s'ennuient.
Parfois, j'envoie ces élèves expliquer aux autres, mais je ne suis pas sûre que leurs explications soient bonnes, puisque la séance suivante, ils ont toujours des difficultés. De plus, leurs "promenades" dans les rangs ne facilitent pas la concentration, d'autant plus que je les ai souvent en dernière heure de l'après midi.
Leur livre comporte de nombreuses méthodes et les exercices restent assez simples, mais pas pour ces élèves en difficulté, et trop faciles pour d'autre élèves qui les font en deux minutes.
Bien sûr, je rajoute des exercices de sésamath ou autres (coloriage magique par exemple) et je les mets une fois par mois en salle info.
Mais certains restent frustrés: l'un d'eux voudrait que je lui apprenne les carrés, racines carrées, ... .
Comment faites-vous face à l'hétérogénéité ?
Quelles ressources pourrais-je utiliser pour ces élèves qui s'ennuient avec ce programme qu'ils ont déjà fait en grande partie au primaire, et prennent plaisir à faire des maths ? Quelle organisation pourrais-je mettre en place ?
Merci pour vos réponses.
 JPhMMDemi-dieu
JPhMMDemi-dieu
De la géométrie pointue en autonomie pour les élèves en demande :
http://www.maths-et-tiques.fr/telech/const_angl.pdf
ou
http://www.apmep.fr/Le-trace-geometrique-au-fil-des
Du GeoGebra :
https://www.neoprofs.org/download.forum?id=4220
http://www.maths-et-tiques.fr/telech/const_angl.pdf
ou
http://www.apmep.fr/Le-trace-geometrique-au-fil-des
Du GeoGebra :
https://www.neoprofs.org/download.forum?id=4220
_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
 cocoonpedaNiveau 7
cocoonpedaNiveau 7
Merci JPhMM pour ces divers liens intéressants.
J'ai une classe de CM2 cette année et je pense que je vais pouvoir donner à réaliser certains de ces tracés à mes élèves
J'ai une classe de CM2 cette année et je pense que je vais pouvoir donner à réaliser certains de ces tracés à mes élèves
_________________
Ce que tu rêves, fais le.
Joseph DELTEIL
 pailleauquebecFidèle du forum
pailleauquebecFidèle du forum
"La géométrie pour le plaisir", travail de tracé en autonomie pour ceux qui ont fini.
http://www.amazon.fr/La-g%C3%A9om%C3%A9trie-pour-plaisir-1/dp/2911327039
Sinon, prendre des problèmes dans la méthode de Singapour CM2 pour avoir du plus difficile (les problèmes sont sans problème du niveau d'un bon élève de 6e). Les problèmes des manuels de 6e actuels sont souvent lamentables.
http://www.lalibrairiedesecoles.com/produit/manuel-de-mathematiques-cm2-cours/
Après il y a aussi les manuels anciens (des années 80, 90 voire avant).
http://manuelsanciens.blogspot.fr/2015/05/lebosse-hemery-arithmetique-et-travaux.html
http://www.priceminister.com/offer/buy/200569/Delord-Robert-Mathematiques-6e-Livre.html
http://www.priceminister.com/offer/buy/60865200/Bonnefond-Gerard---Daviaud-Daniel---Revranche-Bernard-Mathematiques-Pythagore-6e-Edition-1990-Livre.html
Je serais toi je mettrais deux problèmes au tableau, un facile et un difficile.
Les bons élèves ont raison de râler, le programme actuel de 6e est au ras des pâquerettes.
Les manuels actuels que j'ai testé sont aussi très light, pas de vrais cours, pas d'exercices de recherche,... (surtout sur les problèmes dont la réponse est souvent dans la question).
Tu leur feras honneur en leur donnant du biscuit et en nourrissant leur intelligence.
Après ce n'est pas facile, j'ai aussi cette année des élèves particulièrement faibles en 6e (ne savent pas tracer un segment entre deux points, ne savent pas additionner deux nombres à un chiffre, en gros niveau CE1) qui côtoient de très bons.
Je crois qu'on est obligés d'avancer quand même. Honnêtement on est impuissants au delà d'une certaine hétérogénéité.
Mais quelle souffrance! pour ces élèves qu'on envoie au casse pipe au nom du vivre ensemble.
http://www.amazon.fr/La-g%C3%A9om%C3%A9trie-pour-plaisir-1/dp/2911327039
Sinon, prendre des problèmes dans la méthode de Singapour CM2 pour avoir du plus difficile (les problèmes sont sans problème du niveau d'un bon élève de 6e). Les problèmes des manuels de 6e actuels sont souvent lamentables.
http://www.lalibrairiedesecoles.com/produit/manuel-de-mathematiques-cm2-cours/
Après il y a aussi les manuels anciens (des années 80, 90 voire avant).
http://manuelsanciens.blogspot.fr/2015/05/lebosse-hemery-arithmetique-et-travaux.html
http://www.priceminister.com/offer/buy/200569/Delord-Robert-Mathematiques-6e-Livre.html
http://www.priceminister.com/offer/buy/60865200/Bonnefond-Gerard---Daviaud-Daniel---Revranche-Bernard-Mathematiques-Pythagore-6e-Edition-1990-Livre.html
Je serais toi je mettrais deux problèmes au tableau, un facile et un difficile.
Les bons élèves ont raison de râler, le programme actuel de 6e est au ras des pâquerettes.
Les manuels actuels que j'ai testé sont aussi très light, pas de vrais cours, pas d'exercices de recherche,... (surtout sur les problèmes dont la réponse est souvent dans la question).
Tu leur feras honneur en leur donnant du biscuit et en nourrissant leur intelligence.
Après ce n'est pas facile, j'ai aussi cette année des élèves particulièrement faibles en 6e (ne savent pas tracer un segment entre deux points, ne savent pas additionner deux nombres à un chiffre, en gros niveau CE1) qui côtoient de très bons.
Je crois qu'on est obligés d'avancer quand même. Honnêtement on est impuissants au delà d'une certaine hétérogénéité.
Mais quelle souffrance! pour ces élèves qu'on envoie au casse pipe au nom du vivre ensemble.
 JPhMMDemi-dieu
JPhMMDemi-dieu
pailleauquebec a écrit:"La géométrie pour le plaisir", travail de tracé en autonomie pour ceux qui ont fini.
http://www.amazon.fr/La-g%C3%A9om%C3%A9trie-pour-plaisir-1/dp/2911327039
Sinon, prendre des problèmes dans la méthode de Singapour CM2 pour avoir du plus difficile (les problèmes sont sans problème du niveau d'un bon élève de 6e). Les problèmes des manuels de 6e actuels sont souvent lamentables.
http://www.lalibrairiedesecoles.com/produit/manuel-de-mathematiques-cm2-cours/
 J'ai les deux livres (tous les "géométrie pour le plaisir", en fait) et pas mal de photocopies prêtes, extraites de ces livres, en stock dans ma salle pour les élèves qui ont fini.
J'ai les deux livres (tous les "géométrie pour le plaisir", en fait) et pas mal de photocopies prêtes, extraites de ces livres, en stock dans ma salle pour les élèves qui ont fini._________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
 VicomteDeValmontGrand sage
VicomteDeValmontGrand sage
C'est le véritable problème du collège unique, et plus encore aujourd'hui avec le tout inclusion.
_________________
Cette insigne faveur que votre coeur réclame
Nuit à ma renommée et répugne à mon âme.
 thalinaNiveau 3
thalinaNiveau 3
Merci pour vos réponses.
J'ai commandé quelques livres et je vais demander au CDI d'en acheter d'autres.
Mettre deux problèmes au tableau risque de me faire passer plus de temps à la correction, mais c'est une idée que je vais essayer.
J'ai donné une fiche sur des fractales aux élèves les plus rapides (triangle de Sierpiński), rapide à corriger.
J'ai feuilleté le livre de CM2 sur la méthode se Singapour, j'ai trouvé des additions de fractions. Avec la prochaine réforme, on abordera cette notion qu'en quatrième !
J'ai commandé quelques livres et je vais demander au CDI d'en acheter d'autres.
Mettre deux problèmes au tableau risque de me faire passer plus de temps à la correction, mais c'est une idée que je vais essayer.
J'ai donné une fiche sur des fractales aux élèves les plus rapides (triangle de Sierpiński), rapide à corriger.
J'ai feuilleté le livre de CM2 sur la méthode se Singapour, j'ai trouvé des additions de fractions. Avec la prochaine réforme, on abordera cette notion qu'en quatrième !
 pailleauquebecFidèle du forum
pailleauquebecFidèle du forum
C'est un choix, dans notre collège nous aborderons l'addition de fractions même dénominateur et dénominateurs multiples en 6e (cas général pour les bons juste vu au passage, mais pas exigé), cf notre progression détaillée :
https://www.neoprofs.org/t99706-progression-detaillee-mathematiques-cycle-3-6eme-nouveaux-programmes-2016
https://www.neoprofs.org/t99706-progression-detaillee-mathematiques-cycle-3-6eme-nouveaux-programmes-2016
 thalinaNiveau 3
thalinaNiveau 3
J'ai pu acheter le petit livre d'arithmétique de sixième, programme de 1957.
Il sent bon le vieux livre ! Les problèmes sont effectivement d'un autre calibre. Il y a aussi des TP. (Par exemple, pour vérifier des aires, les élèves découpaient des figures géométriques dans du carton puis les pesaient et comparaient).
J'ai acheté aussi le premier tome de la géométrie pour le plaisir. J'hésite à prendre un autre tome, soit avec plus d' illusions d'optiques (mais lequel?), soit sur la géométrie dans l'espace.
J'ai trouvé 100 énigmes logiques et mathématiques du temps du certificat d'études , librairie Larousse. Les problèmes sont ludiques; carrés magiques avec des jeux de dominos ou loto, des problèmes avec des fractions et pourcentages, des problèmes de logique qui demandent à réfléchir, de faire des schémas.
Exemple: "La bonne du curé veut cuire des œufs 9 minutes mais elle ne dispose que de deux sabliers, l'un de 7 minutes et l'autre de 4. Comment va-t-elle s'organiser ?".
Il sent bon le vieux livre ! Les problèmes sont effectivement d'un autre calibre. Il y a aussi des TP. (Par exemple, pour vérifier des aires, les élèves découpaient des figures géométriques dans du carton puis les pesaient et comparaient).
J'ai acheté aussi le premier tome de la géométrie pour le plaisir. J'hésite à prendre un autre tome, soit avec plus d' illusions d'optiques (mais lequel?), soit sur la géométrie dans l'espace.
J'ai trouvé 100 énigmes logiques et mathématiques du temps du certificat d'études , librairie Larousse. Les problèmes sont ludiques; carrés magiques avec des jeux de dominos ou loto, des problèmes avec des fractions et pourcentages, des problèmes de logique qui demandent à réfléchir, de faire des schémas.
Exemple: "La bonne du curé veut cuire des œufs 9 minutes mais elle ne dispose que de deux sabliers, l'un de 7 minutes et l'autre de 4. Comment va-t-elle s'organiser ?".
 thalinaNiveau 3
thalinaNiveau 3
Pourtant, un extrait des programmes des mathématiques, cycle 4, dans la partie "repère de progressivité", dit ceci:pailleauquebec a écrit:C'est un choix, dans notre collège nous aborderons l'addition de fractions même dénominateur et dénominateurs multiples en 6e (cas général pour les bons juste vu au passage, mais pas exigé), cf notre progression détaillée :
https://www.neoprofs.org/t99706-progression-detaillee-mathematiques-cycle-3-6eme-nouveaux-programmes-2016
"Au cycle 3, les élèves ont rencontré des fractions simples sans leur donner le statut de nombre. Dès le
début du cycle 4, les élèves construisent et mobilisent la fraction comme nombre qui rend toutes les
divisions possibles. En 5ème, les élèves calculent et comparent proportions et fréquences, justifient
par un raisonnement l’égalité de deux quotients, reconnaissent un nombre rationnel. À partir de la
4ème, ils sont conduits à additionner, soustraire, multiplier et diviser des quotients, à passer d’une
représentation à une autre d’un nombre, à justifer qu’un nombre est ou non l’inverse d’un autre. Ils
n’abordent la notion de fraction irréductible qu’en 3ème."
C'est pourquoi, même si cela nous a apparu comme une aberration, mes collègues et moi-même avons prévu de faire les additions et soustractions de fractions qu'en 4e.
 Al9Niveau 10
Al9Niveau 10
Je ne comprends pas ta remarque : c'est une aberration mais on va faire ce qu'il recommande 
Chez nous, on a prévu qu'en fin de sixième, on a travaillé la notion de fraction comme nombre (car c'est quand même redondant le programme de cycle 3) et on fait les opérations sur les fractions en 5e (sauf la division).
Non, parce que tout reculer d'un an pour avoir un an de moins pour se l'approprier c'est vrai que c'est une riche idée.

Chez nous, on a prévu qu'en fin de sixième, on a travaillé la notion de fraction comme nombre (car c'est quand même redondant le programme de cycle 3) et on fait les opérations sur les fractions en 5e (sauf la division).
Non, parce que tout reculer d'un an pour avoir un an de moins pour se l'approprier c'est vrai que c'est une riche idée.
 pailleauquebecFidèle du forum
pailleauquebecFidèle du forum
Ces programmes laissent pas mal de libertés.
Reste à savoir s'en saisir.
Pour nous il est clair que la notion de fraction installée en cycle 3 va nécessairement avec les fractions égales donc la simplification.
Et on peut aller en 6e jusqu'à l'addition et la soustraction de fractions.
Après je parle de nos élèves dans notre contexte d'enseignement (pas mal d'heures de marge pour les maths et contexte social favorable).
Les fractions cela demande du temps et de la pratique car c'est difficile pour les élèves.
Je suis pour introduire tôt les notions sur des exemples simples pour les retravailler les années suivantes.
Beaucoup de notions peuvent être vues à plusieurs niveaux d'abstraction.
Reste à savoir s'en saisir.
Pour nous il est clair que la notion de fraction installée en cycle 3 va nécessairement avec les fractions égales donc la simplification.
Et on peut aller en 6e jusqu'à l'addition et la soustraction de fractions.
Après je parle de nos élèves dans notre contexte d'enseignement (pas mal d'heures de marge pour les maths et contexte social favorable).
Les fractions cela demande du temps et de la pratique car c'est difficile pour les élèves.
Je suis pour introduire tôt les notions sur des exemples simples pour les retravailler les années suivantes.
Beaucoup de notions peuvent être vues à plusieurs niveaux d'abstraction.
 AmaliahEmpereur
AmaliahEmpereur
Je suis ce fil avec intérêt, mon fils étant en 6e dans une excellente classe dans laquelle le prof a dit qu'il avancerait bien plus que le programme de 6e. Mais comme je ne suis pas prof de maths, j'ai du mal à repérer ce qui relève de tel ou tel programme et encore plus vu que les programmes changent.
En tout cas, ils ont vu les additions, les multiplications et même les divisions par des fractions en 6e. Les priorités de calculs aussi. Opérations sur les fraction avec ou sans parenthèses. C'est bien, ça m'a fait réviser!
Le titre me laisse songeuse, de même que la formation en Lettres à laquelle j'ai assisté hier : comment les bons élèves peuvent-ils trouver leur compte dans ce collège?
En tout cas, ils ont vu les additions, les multiplications et même les divisions par des fractions en 6e. Les priorités de calculs aussi. Opérations sur les fraction avec ou sans parenthèses. C'est bien, ça m'a fait réviser!
Le titre me laisse songeuse, de même que la formation en Lettres à laquelle j'ai assisté hier : comment les bons élèves peuvent-ils trouver leur compte dans ce collège?
 Al9Niveau 10
Al9Niveau 10
Amaliah a écrit: En tout cas, ils ont vu les additions, les multiplications et même les divisions par des fractions en 6e. Les priorités de calculs aussi. Opérations sur les fraction avec ou sans parenthèses. C'est bien, ça m'a fait réviser!
Tout çà c'est de l'ordre du programme de 5e voire 4e pour les divisions de fractions. Ils doivent être vraiment très bons.
 pailleauquebecFidèle du forum
pailleauquebecFidèle du forum
Amaliah a écrit:Le titre me laisse songeuse, de même que la formation en Lettres à laquelle j'ai assisté hier : comment les bons élèves peuvent-ils trouver leur compte dans ce collège?
Thalina s'interroge, c'est déjà positif. Je lui fais confiance pour trouver des solutions.
 AmaliahEmpereur
AmaliahEmpereur
Je précise mon propos afin qu'il ne soit pas mal interprété! Je me pose la question du sort des bons élèves au collège, y compris dans mes propres classes!!
 Spinoza1670Esprit éclairé
Spinoza1670Esprit éclairé
thalina a écrit:Pourtant, un extrait des programmes des mathématiques, cycle 4, dans la partie "repère de progressivité", dit ceci :pailleauquebec a écrit:C'est un choix, dans notre collège nous aborderons l'addition de fractions même dénominateur et dénominateurs multiples en 6e (cas général pour les bons juste vu au passage, mais pas exigé), cf notre progression détaillée :
https://www.neoprofs.org/t99706-progression-detaillee-mathematiques-cycle-3-6eme-nouveaux-programmes-2016
"Au cycle 3, les élèves ont rencontré des fractions simples sans leur donner le statut de nombre. Dès le début du cycle 4, les élèves construisent et mobilisent la fraction comme nombre qui rend toutes les divisions possibles. En 5ème, les élèves calculent et comparent proportions et fréquences, justifient par un raisonnement l’égalité de deux quotients, reconnaissent un nombre rationnel. À partir de la 4ème, ils sont conduits à additionner, soustraire, multiplier et diviser des quotients, à passer d’une représentation à une autre d’un nombre, à justifier qu’un nombre est ou non l’inverse d’un autre. Ils n’abordent la notion de fraction irréductible qu’en 3ème."
C'est pourquoi, même si cela nous a apparu comme une aberration, mes collègues et moi-même avons prévu de faire les additions et soustractions de fractions qu'en 4e.
- Voici des extraits d'un manuel de ...?
- heu... 4e ?
-
- 5e ?
-
- 6e ?
-
- CM2 ?
-
- CM1 ?
- exact !
- ah enfin j'ai trouvé ! Mais c'est un poisson d'avril, enfin du 3 avril !
-
- Ces manuels étaient utilisés dans des écoles de mutants.
-
Voici des extraits du manuel Brandicourt, Penneçot, Problèmes et calculs CM1 (1963) garanti sans OGM ni P3A* .
Images moyen format (comme ci-dessous) : http://manuelsanciens.blogspot.com/2016/02/brandicourt-pennecot-problemes-et.html
Images grand format : http://manuelsanciens.blogspot.com/2016/02/brandicourt-pennecot-problemes-et_27.html












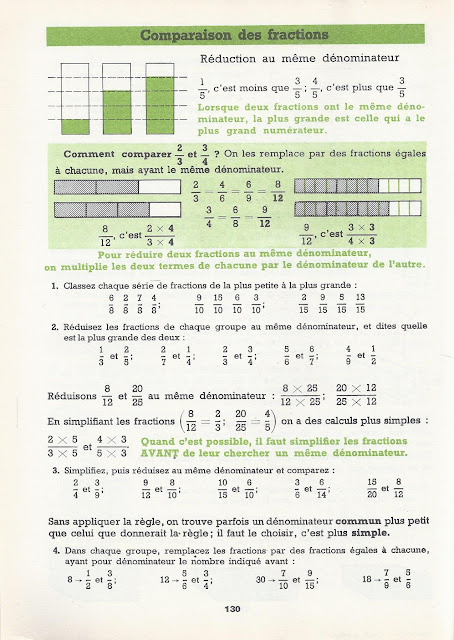







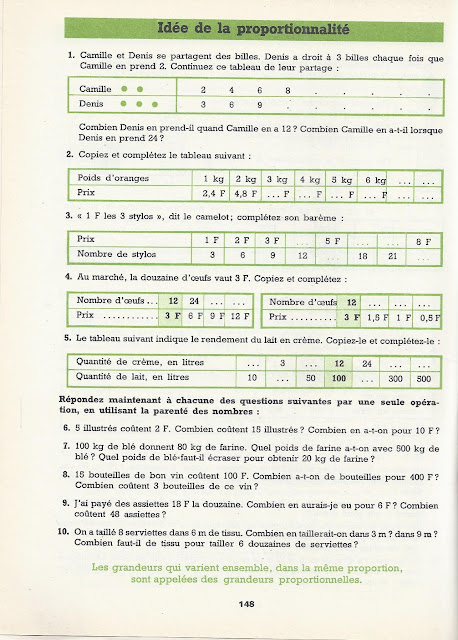



















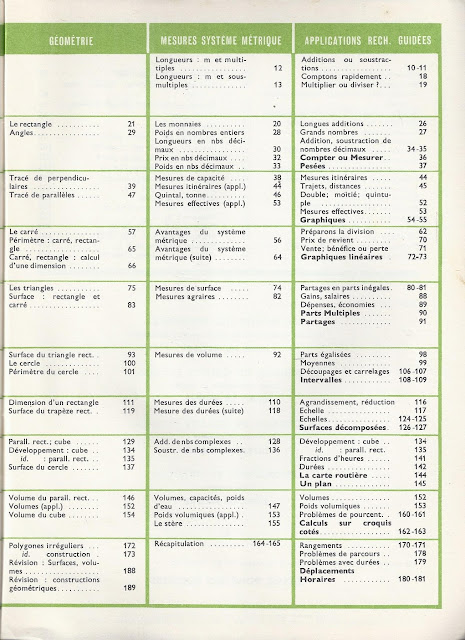
* Poisson du 3 avril.
_________________
« Let not any one pacify his conscience by the delusion that he can do no harm if he takes no part, and forms no opinion. Bad men need nothing more to compass their ends, than that good men should look on and do nothing. » (John Stuart Mill)
Littérature au primaire - Rédaction au primaire - Manuels anciens - Dessin au primaire - Apprendre à lire et à écrire - Maths au primaire - école : références - Leçons de choses.
 LenagcnNiveau 10
LenagcnNiveau 10
En CM2 (bonne classe), nous avons additionné et soustrait des fractions de même dénominateurs. Nous avons fait des additions type "7/12 + ?? = 1" et des soustractions type "1 -4/7 = ". Y compris les "petits oiseaux".
Les meilleurs ont additionné des soustractions à dénominateurs multiples les uns des autres, et quelques têtes chercheuses ont trouvé à additionner des fractions quelconques.
Les meilleurs ont additionné des soustractions à dénominateurs multiples les uns des autres, et quelques têtes chercheuses ont trouvé à additionner des fractions quelconques.
 LenagcnNiveau 10
LenagcnNiveau 10
En élémentaire, il est classique de donner 2 (voire +!) programmes d'exercices différents en parallèle autour d'une même notion.
La gestion du temps, dans la classe et hors classe (cf correction quotidienne du cahier du jour), le permet.
La gestion du temps, dans la classe et hors classe (cf correction quotidienne du cahier du jour), le permet.
 ThalieGrand sage
ThalieGrand sage
Je ne suis pas professeur de Maths mais ne serait-il pas possible de noter la correction sur une fiche afin que les élèves se corrigent en autonomie une fois l'exercice fait ?thalina a écrit:
Mettre deux problèmes au tableau risque de me faire passer plus de temps à la correction, mais c'est une idée que je vais essayer.
Pour Amaliah, la réforme avec l'AP évoque une différenciation nécessaire, comme ce fil le montre il faut nourrir les élèves "experts" comme ils les appellent. J'en conviens mais cela demandera à tous bcp de travail de prévoir au minimun 3 scénarios de cours par heure.
 ZDjNiveau 2
ZDjNiveau 2
Oui je suis moi aussi souvent en difficulté en sixième à cause de l'hétérogénéité. En effet, certains ont le niveau CE1, d'autres ne seraient pas perdu en 5è.
Je trouve qu'il est difficile de différencier, car lorsque l'on donne des exercices supplémentaires aux très bons élèves, il est clair qu'on ne peut pas tous les corriger, et du coup ils travaillent parfois "pour rien", même si c'est pas tout à fait vrai. Alors j'essaie de venir voir ce qu'ils ont fait, mais c'est pas évident de s'occuper des élèves qui ont vraiment besoin de nous et puis de vérifier les nombreux exercices supplémentaires des bons élèves.
Encore, en 6è, ils sont "bonne patte", mais en 3è, les très bons élèves ont plus de mal à faire un exercice supplémentaire, soit parce qu'ils ont la flemme et ne voient pas pourquoi ils en feraient plus que les autres, soit pour ne pas passer pour des "têtes" de classe. Enfin, c'est toutes les joies de l'adolescence.
C'est vrai que donner des problèmes avec un peu de réflexion c'est pas mal mais du coup il faut quand même qu'on soit là pour les guider quand ils sèchent.
Les constructions géométriques c'est une bonne idée, pas sûr que ça fonctionne autant en 3è, mais pour la 5è et la 6è je pense que c'est pas mal.
Je trouve qu'il est difficile de différencier, car lorsque l'on donne des exercices supplémentaires aux très bons élèves, il est clair qu'on ne peut pas tous les corriger, et du coup ils travaillent parfois "pour rien", même si c'est pas tout à fait vrai. Alors j'essaie de venir voir ce qu'ils ont fait, mais c'est pas évident de s'occuper des élèves qui ont vraiment besoin de nous et puis de vérifier les nombreux exercices supplémentaires des bons élèves.
Encore, en 6è, ils sont "bonne patte", mais en 3è, les très bons élèves ont plus de mal à faire un exercice supplémentaire, soit parce qu'ils ont la flemme et ne voient pas pourquoi ils en feraient plus que les autres, soit pour ne pas passer pour des "têtes" de classe. Enfin, c'est toutes les joies de l'adolescence.
C'est vrai que donner des problèmes avec un peu de réflexion c'est pas mal mais du coup il faut quand même qu'on soit là pour les guider quand ils sèchent.
Les constructions géométriques c'est une bonne idée, pas sûr que ça fonctionne autant en 3è, mais pour la 5è et la 6è je pense que c'est pas mal.
Permission de ce forum:
Vous ne pouvez pas répondre aux sujets dans ce forum




