 JPhMMDemi-dieu
JPhMMDemi-dieu
http://www.nature.com/news/first-proof-that-infinitely-many-prime-numbers-come-in-pairs-1.12989
*Vive émotion*





*Vive émotion*





_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
 JPhMMDemi-dieu
JPhMMDemi-dieu
http://annals.math.princeton.edu/articles/7954
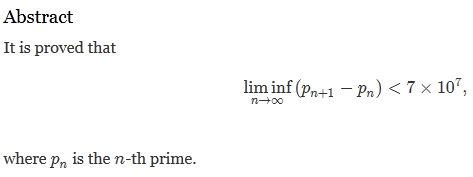
C'est juste magnifique.
:etoilecoeur:






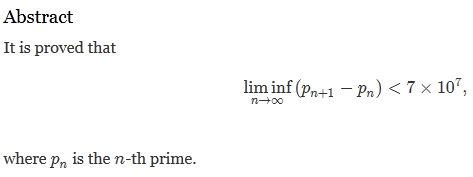
C'est juste magnifique.
:etoilecoeur:







_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
 dandelionVénérable
dandelionVénérable
Ils en ont parlé l'autre jour (je crois vendredi) à la Tête au Carré (chouette émission de vulgarisation scientifique je dois dire, j'ai presque l'impression d'être intelligente quand je l'écouteJPhMM a écrit:http://annals.math.princeton.edu/articles/7954
C'est juste magnifique.
:etoilecoeur:






En même temps, je vois bien les entreprises finançant la recherche s'exclamer: "tout ça pour ça"
 ?
? yphrogEsprit éclairé
yphrogEsprit éclairé
http://www.improbable.com/ig/
 OmbredeloupNiveau 7
OmbredeloupNiveau 7
C'est très intéressant ! J'apprends à la fois l'existence de la conjecture sur l'infinité des nombres premiers jumeaux et cette énorme avancée ! Je vais mettre www.nature.com dans mes favoris.
Merci
Merci
 zinaNiveau 10
zinaNiveau 10
Il ne reste plus que la conjecture sur la fonction Zeta. On approche 

 JPhMMDemi-dieu
JPhMMDemi-dieu
Oui. 

_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
 IgniatiusGuide spirituel
IgniatiusGuide spirituel
Ils ont prouvé que, quel que soit le réel M, il existait toujours deux premiers supérieurs à M dont l'écart était inférieur à 70 millions ?
Ai-je bien pigé ? Je ne suis pas trop certain de ma lecture en anglais.
Si c'est le cas, on est quand même très loin du titre du sujet non ?
Même si la voie semble ouverte...
Ai-je bien pigé ? Je ne suis pas trop certain de ma lecture en anglais.
Si c'est le cas, on est quand même très loin du titre du sujet non ?
Même si la voie semble ouverte...
_________________
"Celui qui se perd dans sa passion est moins perdu que celui qui perd sa passion."
St Augustin
"God only knows what I'd be without you"
Brian Wilson
 JPhMMDemi-dieu
JPhMMDemi-dieu
Il a bien démontré que les couples de nombres premiers (dont les membres sont espacés de moins de 70 millions, certes) sont infiniment nombreux.Igniatius a écrit:Si c'est le cas, on est quand même très loin du titre du sujet non ?
_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
 IgniatiusGuide spirituel
IgniatiusGuide spirituel
JPhMM a écrit:Il a bien démontré que les couples de nombres premiers (dont les membres sont espacés de moins de 70 millions, certes) sont infiniment nombreux.Igniatius a écrit:Si c'est le cas, on est quand même très loin du titre du sujet non ?
OK, merci.
Je n'avais donc pas bien pigé l'article.
Du coup, je ne comprends pas le lien qui semble être fait entre 2 et 70 millions dans l'article.
_________________
"Celui qui se perd dans sa passion est moins perdu que celui qui perd sa passion."
St Augustin
"God only knows what I'd be without you"
Brian Wilson
 Nom d'utilisateurNiveau 10
Nom d'utilisateurNiveau 10
Et question d'ignare (mais la réponse m'intéresserait pour d'autres fins) :
cela signifie-t-il qu'il existe un seuil à partir duquel l'écart entre deux nombres premiers successifs cesse de croître ?
cela signifie-t-il qu'il existe un seuil à partir duquel l'écart entre deux nombres premiers successifs cesse de croître ?
 IgniatiusGuide spirituel
IgniatiusGuide spirituel
Nom d'utilisateur a écrit:Et question d'ignare (mais la réponse m'intéresserait pour d'autres fins) :
cela signifie-t-il qu'il existe un seuil à partir duquel l'écart entre deux nombres premiers successifs cesse de croître ?
Non, je ne crois pas.
_________________
"Celui qui se perd dans sa passion est moins perdu que celui qui perd sa passion."
St Augustin
"God only knows what I'd be without you"
Brian Wilson
 JPhMMDemi-dieu
JPhMMDemi-dieu
L'objectif est de démontrer cette conjecture pour 2. Or pour l'heure elle n'était démontrée pour aucun M. Il faut maintenant réussir à diminuer M jusqu'à 2. Ca va pas être de la tarte, sans nul doute.Igniatius a écrit:JPhMM a écrit:Il a bien démontré que les couples de nombres premiers (dont les membres sont espacés de moins de 70 millions, certes) sont infiniment nombreux.Igniatius a écrit:Si c'est le cas, on est quand même très loin du titre du sujet non ?
OK, merci.
Je n'avais donc pas bien pigé l'article.
Du coup, je ne comprends pas le lien qui semble être fait entre 2 et 70 millions dans l'article.
_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
 JPhMMDemi-dieu
JPhMMDemi-dieu
C'est-à-dire ?Nom d'utilisateur a écrit:Et question d'ignare (mais la réponse m'intéresserait pour d'autres fins) :
cela signifie-t-il qu'il existe un seuil à partir duquel l'écart entre deux nombres premiers successifs cesse de croître ?
_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
 IgniatiusGuide spirituel
IgniatiusGuide spirituel
JPhMM a écrit:L'objectif est de démontrer cette conjecture pour 2. Or pour l'heure elle n'était démontrée pour aucun M. Il faut maintenant réussir à diminuer M jusqu'à 2. Ca va pas être de la tarte, sans nul doute.Igniatius a écrit:JPhMM a écrit:Il a bien démontré que les couples de nombres premiers (dont les membres sont espacés de moins de 70 millions, certes) sont infiniment nombreux.Igniatius a écrit:Si c'est le cas, on est quand même très loin du titre du sujet non ?
OK, merci.
Je n'avais donc pas bien pigé l'article.
Du coup, je ne comprends pas le lien qui semble être fait entre 2 et 70 millions dans l'article.
Ah mais donc, il n'a pas démontré que les premiers jumeaux sont en nombre infini !
C'est juste que les nombres premiers consécutifs avec un écart inférieur à 70 millions sont en nombre infini, c'est bien ça ?
Désolé d'être lourd, mais je veux être sûr de bien piger !
_________________
"Celui qui se perd dans sa passion est moins perdu que celui qui perd sa passion."
St Augustin
"God only knows what I'd be without you"
Brian Wilson
 JPhMMDemi-dieu
JPhMMDemi-dieu
C'est exactement ça.Igniatius a écrit:JPhMM a écrit:L'objectif est de démontrer cette conjecture pour 2. Or pour l'heure elle n'était démontrée pour aucun M. Il faut maintenant réussir à diminuer M jusqu'à 2. Ca va pas être de la tarte, sans nul doute.Igniatius a écrit:JPhMM a écrit:Il a bien démontré que les couples de nombres premiers (dont les membres sont espacés de moins de 70 millions, certes) sont infiniment nombreux.Igniatius a écrit:Si c'est le cas, on est quand même très loin du titre du sujet non ?
OK, merci.
Je n'avais donc pas bien pigé l'article.
Du coup, je ne comprends pas le lien qui semble être fait entre 2 et 70 millions dans l'article.
Ah mais donc, il n'a pas démontré que les premiers jumeaux sont en nombre infini !
C'est juste que les nombres premiers consécutifs avec un écart inférieur à 70 millions sont en nombre infini, c'est bien ça ?
Aucun souci.Igniatius a écrit:Désolé d'être lourd, mais je veux être sûr de bien piger !

_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
 IgniatiusGuide spirituel
IgniatiusGuide spirituel
OK.
En fait, j'avais mal interprété ton titre : j'ai assimilé "in pairs" à "jumeaux".
En fait, j'avais mal interprété ton titre : j'ai assimilé "in pairs" à "jumeaux".
_________________
"Celui qui se perd dans sa passion est moins perdu que celui qui perd sa passion."
St Augustin
"God only knows what I'd be without you"
Brian Wilson
 Nom d'utilisateurNiveau 10
Nom d'utilisateurNiveau 10
JPhMM a écrit:C'est-à-dire ?Nom d'utilisateur a écrit:Et question d'ignare (mais la réponse m'intéresserait pour d'autres fins) :
cela signifie-t-il qu'il existe un seuil à partir duquel l'écart entre deux nombres premiers successifs cesse de croître ?
Pardon, je n'ai saisi qu'à la seconde relecture (ce qui fait bien trois, en l'occurrence) que (a) était tempéré par (b) :
(a) "the gap between each prime and the next becomes larger and larger — on average."
(b) But exceptions exist: the ‘twin primes’, which are pairs of prime numbers that differ in value by 2
Mes rêveries discontinuistes me font lire de travers u__u
 MoonchildSage
MoonchildSage
Igniatius a écrit:Ils ont prouvé que, quel que soit le réel M, il existait toujours deux premiers supérieurs à M dont l'écart était inférieur à 70 millions ?
J'ai un doute là : c'est pas exactement la même chose ?JPhMM a écrit:Il a bien démontré que les couples de nombres premiers (dont les membres sont espacés de moins de 70 millions, certes) sont infiniment nombreux.Igniatius a écrit:Si c'est le cas, on est quand même très loin du titre du sujet non ?
A priori non, l'écart entre deux nombres premiers consécutifs pourrait très bien évoluer de la manière suivante :Nom d'utilisateur a écrit:Et question d'ignare (mais la réponse m'intéresserait pour d'autres fins) :
cela signifie-t-il qu'il existe un seuil à partir duquel l'écart entre deux nombres premiers successifs cesse de croître ?
+2, +10, +2, +100, +2, +1000, +2, +10 000, +2, +100 000, +2, +1 000 000 ...
On aurait alors une infinité de nombres premiers consécutifs dont l'écart serait égal à 2, mais on aurait aussi une infinité de nombres premiers consécutifs dont l'écart ne cesse de croître.
En revanche ce résultat montre que l'écart entre deux nombres premiers consécutifs ne devient pas "systématiquement" de plus en plus grand (i.e. il ne tend pas vers +l'infini).
 JPhMMDemi-dieu
JPhMMDemi-dieu
Oui, et on n'a jamais dit que ce n'était pas la même chose.Moonchild a écrit:Igniatius a écrit:Ils ont prouvé que, quel que soit le réel M, il existait toujours deux premiers supérieurs à M dont l'écart était inférieur à 70 millions ?J'ai un doute là : c'est pas exactement la même chose ?JPhMM a écrit:Il a bien démontré que les couples de nombres premiers (dont les membres sont espacés de moins de 70 millions, certes) sont infiniment nombreux.Igniatius a écrit:Si c'est le cas, on est quand même très loin du titre du sujet non ?
_________________
Labyrinthe où l'admiration des ignorants et des idiots qui prennent pour savoir profond tout ce qu'ils n'entendent pas, les a retenus, bon gré malgré qu'ils en eussent. — John Locke
Je crois que je ne crois en rien. Mais j'ai des doutes. — Jacques Goimard
 MoonchildSage
MoonchildSage
OK.JPhMM a écrit:Oui, et on n'a jamais dit que ce n'était pas la même chose.Moonchild a écrit:Igniatius a écrit:Ils ont prouvé que, quel que soit le réel M, il existait toujours deux premiers supérieurs à M dont l'écart était inférieur à 70 millions ?J'ai un doute là : c'est pas exactement la même chose ?JPhMM a écrit:Il a bien démontré que les couples de nombres premiers (dont les membres sont espacés de moins de 70 millions, certes) sont infiniment nombreux.Igniatius a écrit:Si c'est le cas, on est quand même très loin du titre du sujet non ?
En relisant les messages, j'ai capté que votre divergence d'interprétation initiale portait sur la question des jumeaux.
Permission de ce forum:
Vous ne pouvez pas répondre aux sujets dans ce forum




